2022年3月22日火曜日

テンセグリティ（tensegrity）by バックミンスター・フラー

テンセグリティ - Wikipedia
 
 
最多情報局
⁦‪@tyomateee‬⁩
物理学的に成り立ってるテーブルらしいけど意味不明すぎる pic.twitter.com/xonFbZ2Cue
 
2022/03/22 16:14
 
 
https://twitter.com/tyomateee/status/1506167323467862016?s=21

https://vt.tiktok.com/ZSeHPRyKP/



https://ja.wikipedia.org/wiki/%E3%83%86%E3%83%B3%E3%82%BB%E3%82%B0%E3%83%AA%E3%83%86%E3%82%A3

テンセグリティ

出典: フリー百科事典『ウィキペディア（Wikipedia）』

テンセグリティ（tensegrity）とは、バックミンスター・フラーにより提唱された概念で、Tension（張力）とIntegrity（統合）の造語。実際はケネス・スネルソン（英語版）が彫刻として取り組んでいた引張材と圧縮材からなるオブジェに対し、テンセグリティなる造語を発案し、これを自ら用いたのがバックミンスター・フラーであった。

目次

  • 1 概要
  • 2 脚注
  • 3 参考文献
  • 4 関連項目
  • 5 外部リンク

概要

バックミンスター・フラーはテンセグリティが構造工学における一般的な構造システムのいずれにも分類されないことに気づき、自身の哲学的思想の具体的な表現手段として採用した。テンセグリティは構造システムが破綻しない範囲で、部材を極限まで減らしていったときの最適形状の一種とも考えられている。そのような形状は常識的には三角形を基本単位とするトラスなど単純な幾何学要素の集合であろうと推察されていたから、現代においてもテンセグリティの工学的な視点からの研究は十分ではなく、これからの応用と発展が期待されている。

しばしばバックミンスター・フラーとケネス・スネルソンのいずれが発明者であるかといった議論がなされるが、バックミンスター・フラーのテンセグリティは多面体に類似の対称性の高い形状をしており、一方でケネス・スネルソンのテンセグリティには有機的で不定形な作品が散見され、どちらにも強いオリジナリティが認められる。

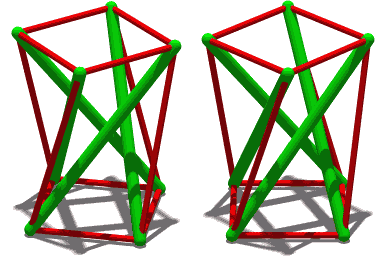
テンセグリティは工学においては直線部材のピン接合からなる構造システムのうち、圧縮材が互いに接続されておらず、張力材とのバランスによって成立しているような構造システムである。張力材は互いに接続されていてもよく、3次元構造の場合、圧縮材の両端には3本以上の張力材が少なくとも接続されていなければならない。

圧縮材は、一般的な構造システムにおいて、柱や張力材を突き上げるためのマストとして用いられ、力強く地面に接地している。テンセグリティにおいては圧縮材は、両端に接続された張力材からの張力によりバランスをとり、他と接触しない。張力材はごく細い材料を選択できるから、まるで圧縮材が空中に浮いているかのような印象的な視覚効果を演出できる。そのような背景と、構造システムとして用いる難易度の高さから、現代ではもっぱら芸術作品や玩具として用いられている[1][2]。

ジェームズ・クラーク・マクスウェルは、自身の提案したトラス構造システムの静定次数と安定次数の計算式には適用範囲が存在し、これを適用できない特殊な形状が存在することを認めている。そのような形状は「何かしらの量を最大もしくは最小にするような特別な形状」であると述べている。テンセグリティはこの記述に合致するため、マクスウェルがテンセグリティを知っていたと解釈することもできる。（実際は直線上にならんだ直線部材などの単純な例を想定していたと考えられる）

脚注

[脚注の使い方]

参考文献

[icon]
この節の加筆が望まれています。

関連項目

[icon]
この節の加筆が望まれています。

外部リンク

[icon]
この節の加筆が望まれています。

Tensegrity - Wikipedia
https://en.wikipedia.org/wiki/Tensegrity

Tensegrity

For the movement system created by Carlos Castaneda, see Tensegrity (Castaneda).
The simplest tensegrity structure (a T3-prism). Each of three compression members (green) is symmetric with the other two, and symmetric from end to end. Each end is connected to three cables (red), which provide tension and precisely define the position of that end in the same way as the three cables in the Skylondefine the bottom end of its tapered pillar.
hideStereo image
Right frame 
hideLeft frame 
Tensegrity simple 4 RL.png
Cross-eye view (Stereogram guide cross-eyed.png)
Parallel view (Stereogram guide parallel.png)
Animation A similar structure but with four compression members.

Tensegrity, tensional integrity or floating compression is a structuralprinciple based on a system of isolated components under compressioninside a network of continuous tension, and arranged in such a way that the compressed members (usually bars or struts) do not touch each other while the prestressed tensioned members (usually cables or tendons) delineate the system spatially.[1]

The term was coined by Buckminster Fuller in the 1960s as a portmanteauof "tensional integrity".[2] The other denomination of tensegrity, floating compression, was used mainly by the constructivist artist Kenneth Snelson.

Contents

  • 1 Concept
  • 2 Applications
  • 3 Biology
  • 4 Origins and art history
  • 5 Stability
    • 5.1 Tensegrity prisms
    • 5.2 Tensegrity icosahedra
  • 6 Patents
  • 7 Basic tensegrity structures
  • 8 Tensegrity structures
  • 9 See also
  • 10 Notes
  • 11 References
  • 12 Bibliography
  • 13 Further reading
  • 14 External links

Concept

Tensegrity structures are based on the combination of a few simple design patterns:

  • members loaded in either pure compression or pure tension, which means that the structure will only fail if the cables yield or the rods buckle. This enables the material properties and cross-sectional geometry of each member to be optimized to the particular load it carries.
  • preload or tensional prestress allows cables to always be in tension, to maintain structural integrity.
  • mechanical stability, which allows the members to remain in tension/compression as stress on the structure increases. The structure also becomes stiffer as cable tension increases.

Because of these patterns, no structural member experiences a bending moment and there are no shear stresses within the system. This can produce exceptionally strong and rigid structures for their mass and for the cross section of the components. The loading of at least some tensegrity structures causes an auxetic response and negative Poisson ratio, e.g. the T3-prism and 6-strut tensegrity icosahedron.

A conceptual building block of tensegrity is seen in the 1951 Skylon. Six cables, three at each end, hold the tower in position. The three cables connected to the bottom "define" its location. The other three cables are simply keeping it vertical.

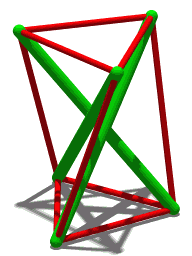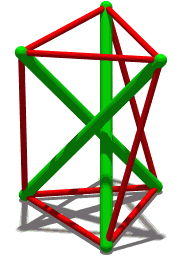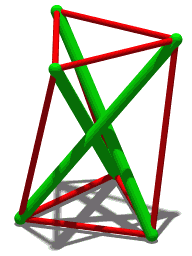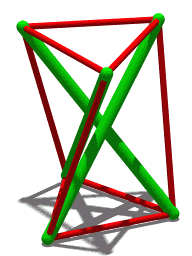
A three-rod tensegrity structure (shown to the right) builds on this simpler structure: the ends of each green rod look like the top and bottom of the Skylon. As long as the angle between any two cables is smaller than 180°, the position of the rod is well defined. While three cables are the minimum required for stability, additional cables can be attached to each node for aesthetic purposes or to build in additional stability. For example, Snelson's Needle Tower uses a repeated pattern built using nodes that are connected to 5 cables each.

Eleanor Heartney points out visual transparency as an important aesthetic quality of these structures.[3] Korkmaz et al. has argued that lightweight tensegrity structures are suitable for adaptive architecture.[4][5]

Applications

Tensegrities saw increased application in architecture beginning in the 1960s, when Maciej Gintowt and Maciej Krasiński designed Spodek arena complex (in Katowice, Poland), as one of the first major structures to employ the principle of tensegrity. The roof uses an inclined surface held in check by a system of cables holding up its circumference. Tensegrity principles were also used in David Geiger's Seoul Olympic Gymnastics Arena (for the 1988 Summer Olympics), and the Georgia Dome (for the 1996 Summer Olympics). Tropicana Field, home of the Tampa Bay Rays major league baseball team, also has a dome roof supported by a large tensegrity structure.

On 4 October 2009, the Kurilpa Bridge opened across the Brisbane Riverin Queensland, Australia. A multiple-mast, cable-stay structure based on the principles of tensegrity, it is currently the world's largest tensegrity bridge.

Since the early 2000s, tensegrities have also attracted the interest of roboticists due to their potential to design lightweight and resilient robots. Numerous researches have investigated tensegrity rovers,[6] bio-mimicking robots,[7][8] and modular soft robots.[9] The most famous tensegrity robot is the Super Ball Bot,[10] a rover for space exploration using a 6-bar tensegrity structure, currently under developments at NASA Ames.

Biology

Biotensegrity, a term coined by Dr. Stephen Levin, is the application of tensegrity principles to biological structures.[11] Biological structures such as muscles, bones, fascia, ligaments and tendons, or rigid and elastic cell membranes, are made strong by the unison of tensioned and compressed parts. The musculoskeletal system maintains tension in a continuous network of muscles and connective tissues,[12] while the bones provide discontinuous compressive support. Even the human spine, which seems at first glance like a stack of vertebrae resting on each other, is actually a tensegrity structure.[13]

Donald E. Ingber has developed a theory of tensegrity to describe numerous phenomena observed in molecular biology.[14] For instance, the expressed shapes of cells, whether it be their reactions to applied pressure, interactions with substrates, etc., all can be mathematically modeled by representing the cell's cytoskeleton as a tensegrity. Furthermore, geometric patterns found throughout nature (the helix of DNA, the geodesic dome of a volvox, Buckminsterfullerene, and more) may also be understood based on applying the principles of tensegrity to the spontaneous self-assembly of compounds, proteins,[15] and even organs. This view is supported by how the tension-compression interactions of tensegrity minimize material needed to maintain stability and achieve structural resiliency.[16] Therefore, natural selection pressures would likely favor biological systems organized in a tensegrity manner.

As Ingber explains:

The tension-bearing members in these structures – whether Fuller's domes or Snelson's sculptures – map out the shortest paths between adjacent members (and are therefore, by definition, arranged geodesically). Tensional forces naturally transmit themselves over the shortest distance between two points, so the members of a tensegrity structure are precisely positioned to best withstand stress. For this reason, tensegrity structures offer a maximum amount of strength.[14]

In embryology, Richard Gordon proposed that Embryonic differentiation waves are propagated by an 'organelle of differentiation'[17] where the cytoskeleton is assembled in a bistable tensegrity structure at the apical end of cells called the 'cell state splitter'.[18]

Origins and art history

Kenneth Snelson's 1948 X-Module Design as embodied in a two-module column[19]

The origins of tensegrity are controversial.[20] Many traditional structures, such as skin-on-frame kayaks and shōji, use tension and compression elements in a similar fashion.

Russian artist Viatcheslav Koleichuk claimed that the idea of tensegrity was invented first by Kārlis Johansons (in Russian as German as Karl Ioganson) (lv), a Soviet avant-garde artist of Latvian descent, who contributed some works to the main exhibition of Russian constructivism in 1921.[21] Koleichuk's claim was backed up by Maria Gough for one of the works at the 1921 constructivist exhibition.[22] Snelson has acknowledged the constructivists as an influence for his work (query?).[23] French engineer David Georges Emmerich has also noted how Kārlis Johansons's work (and industrial design ideas) seemed to foresee tensegrity concepts.[24]

In 1948, artist Kenneth Snelson produced his innovative "X-Piece" after artistic explorations at Black Mountain College (where Buckminster Fullerwas lecturing) and elsewhere. Some years later, the term "tensegrity" was coined by Fuller, who is best known for his geodesic domes. Throughout his career, Fuller had experimented with incorporating tensile components in his work, such as in the framing of his dymaxion houses.[25]

Snelson's 1948 innovation spurred Fuller to immediately commission a mast from Snelson. In 1949, Fuller developed a tensegrity-icosahedronbased on the technology, and he and his students quickly developed further structures and applied the technology to building domes. After a hiatus, Snelson also went on to produce a plethora of sculptures based on tensegrity concepts. His main body of work began in 1959 when a pivotal exhibition at the Museum of Modern Art took place. At the MOMA exhibition, Fuller had shown the mast and some of his other work.[26] At this exhibition, Snelson, after a discussion with Fuller and the exhibition organizers regarding credit for the mast, also displayed some work in a vitrine.[27]

Snelson's best known piece is his 18-meter-high Needle Tower of 1968.

Stability

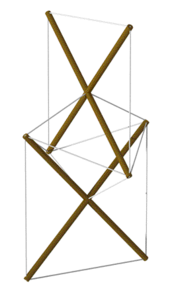
Tensegrity prisms

The three-rod tensegrity structure (3-way prism) has the property that, for a given (common) length of compression member “rod” (there are three total) and a given (common) length of tension cable “tendon” (six total) connecting the rod ends together, there is a particular value for the (common) length of the tendon connecting the rod tops with the neighboring rod bottoms that causes the structure to hold a stable shape. For such a structure, it is straightforward to prove that the triangle formed by the rod tops and that formed by the rod bottoms are rotated with respect to each other by an angle of 5π/6 (radians).[28]

The stability (“prestressability”) of several 2-stage tensegrity structures are analyzed by Sultan, et al.[29]

Tensegrity icosahedra

A tensegrity icosahedron made from straws and string

The tensegrity icosahedron, first studied by Snelson in 1949,[30] has struts and tendons along the edges of a polyhedron called Jessen's icosahedron. It is a stable construction, albeit with infinitesimal mobility.[31] To see this, consider a cube of side length 2d, centered at the origin. Place a strut of length 2l in the plane of each cube face, such that each strut is parallel to one edge of the face and is centered on the face. Moreover, each strut should be parallel to the strut on the opposite face of the cube, but orthogonal to all other struts. If the Cartesian coordinates of one strut are and , those of its parallel strut will be, respectively, and . The coordinates of the other strut ends (vertices) are obtained by permuting the coordinates, e.g., (rotational symmetry in the main diagonal of the cube).

The distance s between any two neighboring vertices (0, d, l) and (d, l, 0) is

Imagine this figure built from struts of given length 2l and tendons (connecting neighboring vertices) of given length s, with . The relation tells us there are two possible values for d: one realized by pushing the struts together, the other by pulling them apart. In the particular case the two extremes coincide, and , therefore the figure is the stable tensegrity icosahedron. This choice of parameters gives the vertices the positions of Jessen's icosahedron; they are different from the regular icosahedron, for which the ratio of  and would be the golden ratio, rather than 2. However both sets of coordinates lie along a continuous family of positions ranging from the cuboctahedronto the octahedron (as limit cases), described by H. S. M. Coxeter[32] and later called the "jitterbug motion" by Buckminster Fuller.[33][34]

Since the tensegrity icosahedron represents an extremal point of the above relation, it has infinitesimal mobility: a small change in the length s of the tendon (e.g. by stretching the tendons) results in a much larger change of the distance 2d of the struts.

Patents

  • U.S. Patent 3,063,521, "Tensile-Integrity Structures," 13 November 1962, Buckminster Fuller.
  • French Patent No. 1,377,290, "Construction de Reseaux Autotendants", 28 September 1964, David Georges Emmerich.
  • French Patent No. 1,377,291, "Structures Linéaires Autotendants", 28 September 1964, David Georges Emmerich.
  • U.S. Patent 3,139,957, "Suspension Building" (also called aspension), 7 July 1964, Buckminster Fuller.
  • U.S. Patent 3,169,611, "Continuous Tension, Discontinuous Compression Structure," 16 February 1965, Kenneth Snelson.
  • U.S. Patent 3,866,366, "Non-symmetrical Tension-Integrity Structures," 18 February 1975, Buckminster Fuller.

Basic tensegrity structures

  • The simplest tensegrity structure, a 3-prism

  • Another 3-prism

  • A similar structure but with four compression members

  • Proto-Tensegrity Prism by Karl Ioganson, 1921[gallery 1]

  • Tensegrity Icosahedron, Buckminster Fuller, 1949[gallery 2]

  • Tensegrity Tetrahedron, Francesco della Salla, 1952[gallery 3]

  • Tensegrity X-Module Tetrahedron, Kenneth Snelson, 1959[gallery 4]

Tensegrity structures

  • Kenneth Snelson's Needle Tower art sculpture.

  • A tensegrity dome made of garden stakes and nylon twine built in the yard of a house, 2009

  • A 12m high tensegrity structure exhibit at the Science City, Kolkata.

  • Dissipate, an hourglass tower art sculpture including tensegrity structure, constructed at AfrikaBurn, 2015, a Burning Man regional event

See also

Notes

  1.  Gómez-Jáuregui 2010, p. 28. Fig. 2.1
  2.  Fuller & Marks 1960, Fig. 270
  3.  Fuller & Marks 1960, Fig. 268.
  4.  Lalvani 1996, p. 47

References

  1.  Gómez-Jáuregui 2010, p. 19.
  2.  Swanson, RL (2013). "Biotensegrity: a unifying theory of biological architecture with applications to osteopathic practice, education, and research-a review and analysis". The Journal of the American Osteopathic Association. 113 (1): 34–52. doi:10.7556/jaoa.2013.113.1.34. PMID 23329804.
  3.  Eleanor Hartley, "Ken Snelson and the Aesthetics of Structure," in the Marlborough Gallery catalogue for Kenneth Snelson: Selected Work: 1948–2009, exhibited 19 February through 21 March 2009.
  6.  Sabelhaus, Andrew P.; Bruce, Jonathan; Caluwaerts, Ken; Manovi, Pavlo; Firoozi, Roya Fallah; Dobi, Sarah; Agogino, Alice M.; SunSpiral, Vytas (May 2015). "System design and locomotion of SUPERball, an untethered tensegrity robot". 2015 IEEE International Conference on Robotics and Automation (ICRA). Seattle, WA, USA: IEEE: 2867–2873. doi:10.1109/ICRA.2015.7139590. hdl:2060/20160001750. ISBN 978-1-4799-6923-4. S2CID 8548412.
  7.  Lessard, Steven; Castro, Dennis; Asper, William; Chopra, Shaurya Deep; Baltaxe-Admony, Leya Breanna; Teodorescu, Mircea; SunSpiral, Vytas; Agogino, Adrian (October 2016). "A bio-inspired tensegrity manipulator with multi-DOF, structurally compliant joints". 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE: 5515–5520. arXiv:1604.08667. doi:10.1109/iros.2016.7759811. ISBN 978-1-5090-3762-9. S2CID 4507700.
  8.  Zappetti, Davide; Arandes, Roc; Ajanic, Enrico; Floreano, Dario (5 June 2020). "Variable-stiffness tensegrity spine". Smart Materials and Structures. 29 (7): 075013. Bibcode:2020SMaS...29g5013Z. doi:10.1088/1361-665x/ab87e0. ISSN 0964-1726.
  9.  Zappetti, D.; Mintchev, S.; Shintake, J.; Floreano, D. (2017), "Bio-inspired Tensegrity Soft Modular Robots", Biomimetic and Biohybrid Systems, Cham: Springer International Publishing, pp. 497–508, arXiv:1703.10139, doi:10.1007/978-3-319-63537-8_42, ISBN 978-3-319-63536-1, S2CID 822747, retrieved 17 June 2020
  10.  Hall, Loura (2 April 2015). "Super Ball Bot". NASA. Retrieved 18 June2020.
  11.  Levin, Stephen (2015). "16. Tensegrity, The New Biomechanics". In Hutson, Michael; Ward, Adam (eds.). Oxford Textbook of Musculoskeletal Medicine. Oxford University Press. pp. 155–56, 158–60. ISBN 978-0-19-967410-7.
  12.  Souza et al. 2009.
  13.  Levin, Stephen M. (1 September 2002). "The tensegrity-truss as a model for spine mechanics: biotensegrity". Journal of Mechanics in Medicine and Biology. 02 (3n04): 375–88. doi:10.1142/S0219519402000472. ISSN 0219-5194.
  14. ^ a b Ingber, Donald E. (January 1998). "The Architecture of Life"(PDF). Scientific American. 278 (1): 48–57. Bibcode:1998SciAm.278a..48I. doi:10.1038/scientificamerican0198-48. PMID 11536845. Archived from the original (PDF) on 15 May 2005.
  15.  Edwards, Scott A.; Wagner, Johannes; Gräter, Frauke (2012). "Dynamic Prestress in a Globular Protein". PLOS Computational Biology. 8 (5): e1002509. Bibcode:2012PLSCB...8E2509E. doi:10.1371/journal.pcbi.1002509. PMC 3349725. PMID 22589712.
  16.  Skelton, Robert (2016). "Globally stable minimal mass compressive tensegrity structures". Composite Structures. 141: 346–54. doi:10.1016/j.compstruct.2016.01.105.
  17.  Gordon, Natalie K.; Gordon, Richard (2016). "The organelle of differentiation in embryos: The cell state splitter". Theoretical Biology and Medical Modelling. 13: 11. doi:10.1186/s12976-016-0037-2. PMC 4785624. PMID 26965444.
  18.  Gordon, Richard (1999). The Hierarchical Genome and Differentiation Waves. Series in Mathematical Biology and Medicine. Vol. 3. doi:10.1142/2755. ISBN 978-981-02-2268-0.
  19.  Gough 1998, p. 109.
  20.  Gómez-Jáuregui, V. (2009). "Controversial Origins of Tensegrity"(PDF). International Association of Spatial Structures IASS Symposium 2009, Valencia.
  21.  Droitcour, Brian (18 August 2006). "Building Blocks". The Moscow Times. Archived from the original on 7 October 2008. Retrieved 28 March 2011. With an unusual mix of art and science, Vyacheslav Koleichuk resurrected a legendary 1921 exhibition of Constructivist art.
  22.  Gough 1998.
  23.  In Snelson's article for Lalvani, 1996, I believe.[full citation needed]
  24.  David Georges Emmerich, Structures Tendues et Autotendantes, Paris: Ecole d'Architecture de Paris la Villette, 1988, pp. 30–31.
  25.  Fuller & Marks 1960, Ch. Tensegrity.
  26.  See photo of Fuller's work at this exhibition in his 1961 article on tensegrity for the Portfolio and Art News Annual (No. 4).
  27.  Lalvani 1996, p. 47.
  28.  Burkhardt, Robert William, Jr. (2008), A Practical Guide to Tensegrity Design (PDF)
  29.  Sultan, Cornel; Martin Corless; Robert E. Skelton (2001). "The prestressability problem of tensegrity structures: some analytical solutions" (PDF). International Journal of Solids and Structures. 26: 145. Archived from the original (PDF) on 23 October 2015.
  30.  Cera, Angelo Brian Micubo (2020). Design, Control, and Motion Planning of Cable-Driven Flexible Tensegrity Robots (Ph.D. thesis). University of California, Berkeley. p. 5.
  31.  "Tensegrity Figuren". Universität Regensburg. Archived from the original on 26 May 2013. Retrieved 2 April 2013.
  32.  Coxeter, H.S.M. (1973) [1948]. "3.7 Coordinates for the vertices of the regular and quasi-regular solids". Regular Polytopes (3rd ed.). New York: Dover. pp. 51–52.
  33.  Archived at Ghostarchive and the Wayback Machine: Fuller, R. Buckminster (22 October 2010), Vector Equilibrium, retrieved 22 February 2019
  34.  Verheyen, H.F. (1989). "The complete set of Jitterbug transformers and the analysis of their motion". Computers & Mathematics with Applications. 17, 1–3 (1–3): 203–250. doi:10.1016/0898-1221(89)90160-0.

Bibliography

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations.  (March 2009) (Learn how and when to remove this template message)

Further reading

External links

Wikimedia Commons has media related to Tensegrity.

時刻:

0 件のコメント:

コメントを投稿

登録: コメントの投稿 (Atom)