《機能的財政がなすところのことは、一原則を政治の裁量に置き換えることではなく、むしろ一つの原則を別の原則に置き換えることである。機能的財政は、当局に対して、収入に等しい経費を維持することのかわりに、別の原則にしたがって、しかも完全雇用をもたらしインフレーションを避ける水準に、総支出率を維持することを告げるのである。…それは政府の力を増加させるものではない。それは、政府がすでにもっていた力に対する責任を、政府に認識させることを要求するものにすぎない。》ラーナー『雇用の経済学』邦訳218頁
四つの元の限界値:越村1989(後述)61頁より
| _ー 消費者の想定的限界費用 マルサス(3)(4)
| _ー ̄
| _ー ̄
|_ー ̄ |
| | /生産者の限界費用 マルクス(5)
|\ | /
| \ | /供給曲線
| \ | /
| \|/
|均衡数量X←均衡点
| /|\
| / |均\ 需要曲線
| / |衡 \
|/ |価 \消費者の限界効用 ワルラス(1)(2)
|____|格___\___
0 生産者の
限界効用 プルードン(0)
厚 生 方 程 式
┏━━━完全に中央集権的な経済によって直接的に等しくされる━━━┓
┃分権的ではあるが集産主義的な経済の「原則」によって等しくされる┃ ┃ ┏━━━━━━━━┻━━━━━━━━━━┓ ┃
msb社会的 = vmp限界生 = mpr私的 = mpc私的 = vmf限界要 = msc社会
限界利益 産物の価値 限界収入 限界費用 因の価値 的限界費用
(1) (2) (3) (4) (5)
生産された財 生産物の販売に 利潤の 生産要因の購
費の最適配分 おける完全競争 極大化 入における完
全競争
(5)以上の四個の方程式が要因の二者択一的な用途で満たされるので、
二者択一的な諸用途においてvmf限界要因の価値=msb社会的限界利益である。
厚 生 方 程 式
┏━━━━━完全に中央集権的な経済によって直接的に等しくされる。━━━━━┓
┃ 分権的ではあるが集産主義的な経済の「原則」によって等しくされる。 ┃
┃ ┏━━━━━━━━━┻━━━━━━━━━━┓ ┃
msb社会的 = vmp限界生 = mpr私的 = mpc私的 = vmf限界要 = msc社会的
限界利益 産物の価値 限界収入 限界費用 因の価値 限界費用
(1) (2) (3) (4) (5)
生産された財 生産物の販売に 利潤の 生産要因の購
費の最適配分 おける完全競争 極大化 入における完
全競争
(5)以上の四個の方程式が要因の二者択一的な用途で満たされるので、
二者択一的な諸用途においてvmf限界要因の価値=msb社会的限界利益である。
公共経済学ノート
https://sites.google.com/site/marutaro777/home/public?tmpl=%2Fsystem%2Fapp%2Ftemplates%2Fprint%2F&showPrintDialog=1 ★
● 「常木淳 公共経済学 新世社 第2版 2002/03」
7章2節、効用関数を同一と見なせるかどうかにおけるラーナーの議論が重要で、
柴田公共ではP224~P227で説明される。
林公共のP278~P280にも、同質の効用関数に関する議論があり、
特にP280の「第2」は、ラーナーの議論に相当する。
ベンサム型とロールズ型の説明については、板谷公共の3章5節~8節(p79~p97)も参照。
[対抗投機も底上げではなく損失となる三角形の拡大と捉えるべきか]7章2節、効用関数を同一と見なせるかどうかにおけるラーナーの議論が重要で、
柴田公共ではP224~P227で説明される。
林公共のP278~P280にも、同質の効用関数に関する議論があり、
特にP280の「第2」は、ラーナーの議論に相当する。
ベンサム型とロールズ型の説明については、板谷公共の3章5節~8節(p79~p97)も参照。
(ラーナーの図は慣例と違い価格が横軸)
ラーナーはパレート最適からズレる
常木公共初版
#6.2:140頁
dU^h/dW^h
各人の効用はU^hは彼の富W^hの関数であると仮定
10:
★
【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する | どさんこ北国の経済教室
https://kitaguni-economics.com/profit-maximization/【完全競争・利潤最大化】条件や求め方・計算方法をグラフを使って理解する
「完全競争市場の利潤最大化」
- 利潤最大化の意味
- 利潤最大化の考え方
- 利潤最大化で微分が登場する理由
- 利潤最大化条件の計算方法
- 利潤最大化と限界生産力(MP)
- 費用関数から利潤最大化を求める
- 生産関数から利潤最大化を求める
生産者理論で重要な項目の1つである「利潤最大化」についての情報を、簡単に分かりやすくまとめました。
利潤最大化とは?
利潤最大化とは?
企業は、自社の利潤を最大化するために生産活動を行う。これを「利潤最大化(企業の利潤最大化行動)」と呼ぶ。また、その利潤最大化を求める問題・それに関連する問題を「利潤最大化問題」と呼ぶ。
北国宗太郎
牛さん
利潤は「機会費用」を考慮している
機会費用
複数の選択肢のうち自分が選んでいない選択肢で得られたはずの利益のこと
企業が自社で保有している土地を
- 畑にする?
- 工場にする?
と迷っていた時を考えます。
結局100万円かけて工場を建設して商品を生産しました。しかし、商品は全く売れませんでした。
このとき「利益」を計算するには工場を建てる時に発生した「100万円」を使います。⇒「利益=-100万円」
「利潤」は、建設費「100万円」+「仮に、畑にして作物を作っていた時に得られていただろう利益」も考慮して計算します。
ポイント
畑にしていれば1,000万円の利益は確実に得られたなら「利益を逃した=費用」と考えます。工場の建設費100万円と合わせて「利潤=-1,100万円」と考えます。
北国宗太郎

牛さん
ただし
- 利潤・利益の違いはそんなに気にしなくてよい
ミクロ経済学で登場する「利潤最大化問題」では「利潤=利益」と考えて差し支えないので、気にせずに計算を進めてOKです。
利潤最大化条件
完全競争市場における利潤最大化が理解出来ない人向けに
- そもそもの考え方
- 実際の文字式で考える
2つの段階に分けて説明をしていきます。
ここを理解すると、利潤最大化で微分する理由、計算過程で「=0」とする理由も分かります
①考え方を理解する
利潤を求めるには
⇒「全ての収入」から「全ての費用」を引けば利潤になる!
つまり「利潤(π)=総収入-総費用」となります。基本はこの式をもとに考えを進めていくので、しっかりと押さえましょう。
次は具体例をもとに話を進めていきます。
例えば
- ある企業が自動車の生産販売を行っています
この企業は、自動車の大量生産を実現しており、手ごろな価格で車を販売しています。
生産を拡大していけば、生産効率が上がるため費用を押さえて生産を行うことが出来ます。そのため、大量生産が実現すれば安く商品を提供できます。
- この時、企業は作って売れば売るほど利潤が発生します
北国宗太郎
それなら、無限に生産すれば利潤が最大化するって考えるのかな?
牛さん
この企業は、無理に生産販売を続けた結果、生産効率が落ちていき費用が余計に掛かるようになりました。
このように、無理な生産拡大は費用の逓増をもたらします。
費用(総費用)については、こちらで確認できます⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界
- 完全競争市場ではライバル企業が多数いるため、安易に値上げ出来ません
市場の相場によって販売価格(P)が決まり、大きく変動することは基本はありません。企業はこの市場価格を受け入れるため、完全競争市場では企業はプライステイカー(価格受容者)と考えて、販売価格は一定だと仮定します。
- 総収入と総費用の関係は次のようになります
①販売価格(P)が一定なので、生産量(Q)を増やして販売すれば、常に一定の収入増となります。総収入曲線(TR)は右上がりの直線。
②規模を拡大しすぎると生産が非効率となるため、生産量(Q)を増やし過ぎたあたりから、急激に増加します。総費用曲線(TC)は右上がりの曲線。
③そして、利潤(π)は「総収入(TR)-総費用(TC)」なので、この2つのグラフの差の部分(黄緑色の矢印)が利潤だと分かります。
北国宗太郎
牛さん
- 限界収入(MR)と限界費用(MC)で考える
ここまでは、総収入(TR)と総費用(TC)で話を進めてきましたが、少し細かく見ていきます。ここを理解すると、利潤最大化問題で微分をする理由が分かります。
まずは、矢印が一番長くなる瞬間のグラフを見てみましょう。
総収入曲線(TR)と総費用曲線(TC)の傾きが同じになった瞬間に利潤最大化が実現します。
総収入曲線・総費用曲線の「傾き」がキーワードになります。「傾き」と限界収入(MR)と限界費用(MC)の関係について順番に見ていきましょう。
step
1「総収入曲線の傾き=限界収入」について
1「総収入曲線の傾き=限界収入」について
先ほど説明した通り、完全競争市場では販売価格(P)は一定なので、収入の増加は常に一定です。
- 1台100万円の車を販売する
すると、1台生産をして販売すれば100万円の収入増になります。
ここで2つ重要なことがあります。
- 総収入曲線(TR)の傾きです
1台生産をして販売すれば100万円の収入増になるため、直線の式は次のようになります。
- 総収入曲線(TR)=100万円×生産量(Q)
この時、総収入曲線(TR)の「傾き=100万」となります。
※ちなみに、傾きの求め方は「(傾き)=縦軸÷横軸=100万÷1台=100万」

北国宗太郎
「Y=2X」なら”傾き=2”っていうのと同じだね。

牛さん
自動車を1台売ったときに発生する、売上の増加分のこと(生産物を1単位当たり売却した時に得られる収入の増加分)を限界収入(MR)と呼びます。
つまり、この100万は「傾き」であると同時に「限界収入(MR)」になります。
※限界収入(MR)の詳しい解説についてはこちら⇒限界収入とは?
ポイント
- 「総収入曲線(TR)の傾き」=「限界収入(MR)」
ちなみに、経済学で登場する「限界●●」は「傾き」と同じことを意味します。

北国宗太郎
なんとなく分かりました。総費用曲線でも同じ考え方を使うの?

牛さん
step
2「総費用曲線の傾き=限界費用」について
2「総費用曲線の傾き=限界費用」について
先ほど説明した通り、総費用曲線(TC)は、生産の効率性によって増加具合が変化します。
つまり、生産が効率的か・過剰生産かによって費用が変化する

北国宗太郎
グラフがカーブを描いているから「傾き」が分からないよね。

牛さん
先ほどは、具体的に「1台生産したとき」と考えましたが、それでは傾きが分かりません。そこで「1台生産したとき」と考えず「1よりも小さい点」で考えます。
このように「ある点に対して接線を引いて、その傾き」を求めます。
先ほどと同じように「総費用曲線(TC)の接線の傾き=限界費用(MC)」となります。
ポイント
- 「総費用曲線(TC)の傾き」=「限界費用(MC)」
先ほどの例で考えれば自動車を1台生産したときに発生する、費用の増加分のこと(生産物を1単位当たり生産した時に発生する費用の増加分)を限界費用(MC)と呼びます。
限界費用(MC)の詳しい解説はこちら⇒限界費用とは?利益・平均費用との関係も分かりやすく簡単に解説
これではイメージしづらいと思いますので、先ほどの自動車の例で考えます。
例えば①
- 1台100万円の車を販売する
- この1台の製造費は60万円
1台販売して、収入が100万円増加するため「限界収入(MR)=100万円」
1台生産して、費用が60万円増加するため「限界費用(MC)=60万円」
1台生産して、費用が60万円増加するため「限界費用(MC)=60万円」
- この1台を販売したことで利潤(π)が「40万円」増加します
ポイント
ここで、限界収入(MR)が限界費用(MC)より大きければ利潤がプラスになるため、その1台を製造販売した方が利潤が増加することが分かる。
- 総収入曲線(TR)の傾き=限界収入(MR)=100万円
- 総費用曲線(TC)の傾き=限界費用(MC)=60万円
「総収入曲線(TR)の傾き>総費用曲線(TC)の傾き」となっていることが分かります。
例えば②
- もう1台車を100万円で販売する
- この1台の製造費は100万円かかった
1台販売して、収入が100万円増加するため「限界収入(MR)=100万円」
1台生産して、費用が100万円増加するため「限界費用(MC)=100万円」
1台生産して、費用が100万円増加するため「限界費用(MC)=100万円」
- この1台を販売しても利潤(π)は「0円」です
ポイント
限界収入(MR)と限界費用(MC)が同じ金額になるとき、利潤が発生しない。
- 総収入曲線(TR)の傾き=限界収入(MR)=100万円
- 総費用曲線(TC)の傾き=限界費用(MC)=100万円
「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」となっていることが分かります。
例えば③
- もう1台車を100万円で販売する
- この1台の製造費は150万円かかった
1台販売して、収入が100万円増加するため「限界収入(MR)=100万円」
1台生産して、費用が150万円増加するため「限界費用(MC)=150万円」
1台生産して、費用が150万円増加するため「限界費用(MC)=150万円」
- この1台を販売しても利潤(π)は「-50万円」です
ポイント
ここで、限界収入(MR)より限界費用(MC)の金額が大きくなるとき利潤がマイナスになるため、その1台は製造販売しない方が良かったことが分かる。
- 総収入曲線(TR)の傾き=限界収入(MR)=100万円
- 総費用曲線(TC)の傾き=限界費用(MC)=150万円
「総収入曲線(TR)の傾き<総費用曲線(TC)の傾き」となっていることが分かります。
step
3「価格=限界収入=限界費用」について
3「価格=限界収入=限界費用」について
まとめ
- 例①~③をまとめると‥
①「総収入曲線(TR)の傾き>総費用曲線(TC)の傾き」⇒追加の利潤がプラス
②「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」⇒追加の利潤が0円
③「総収入曲線(TR)の傾き<総費用曲線(TC)の傾き」⇒追加の利潤がマイナス
追加の利潤が0円になるまで製造販売を行えば、利潤を拡大することが出来る。別の言い方をすれば、利潤が0円になるまで製造販売をすれば、利潤が最大化する。
グラフで考えれば「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」になるまで製造販売すればOK。
更に…
- 総収入曲線(TR)の傾き=限界収入(MR)
- 総費用曲線(TC)の傾き=限界費用(MC)
となるため「限界収入(MR)=限界費用(MC)」で利潤が最大化するとも言えます。
完全競争市場では、限界収入(MR)は販売価格(P)と同じです。
販売価格(P)=100円の商品を、追加で1つ売ったら収入が100円増加します(価格=限界収入=100円)。最初に説明した通り、完全競争市場ではライバル企業が多数いるため、安易に値上げが出来ません。市場の相場によって販売価格(P)が決まり、大きく変動することは基本ありません。そのため、完全競争市場では販売価格(P)は常に一定と考えました。販売価格(P)が常に一定なら、商品を何個売ろうが、増加する収入(限界収入)も一定になります。つまり「販売価格(P)=限界収入(MR)」です。
以上より
- 総収入曲線(TR)の傾き=限界収入(MR)=価格(P)
- 総費用曲線(TC)の傾き=限界費用(MC)
となるため「価格(P)=限界費用(MC)」で利潤が最大化するとも言えます。
利潤最大化条件
この「価格(P)=限界費用(MC)」を利潤最大化条件(1階条件)と言います。
つまり、利潤最大化が実現するとき「価格(P)=限界収入(MR)=限界費用(MC)」が実現することになります。この部分は重要なので、しっかりと理解しましょう。イメージが湧かない人はこちらでも確認できます⇒【価格=限界費用=限界収入】なぜ完全競争市場で「P=MC=MR」となるのか

北国宗太郎

牛さん
step
4微分について
4微分について
これまでの説明から、利潤最大化を求めるには「総収入曲線(TR)の傾き・総費用曲線(TC)の傾き」を求めれば良いことが分かったかと思います。
ここで、この傾きを求めるために「微分」が登場します。
この2つの傾きは微分をすれば求められる
通常、傾きは次の式で求められます。
- 傾き=(縦軸に移動した距離)÷(横軸に移動した距離)
ただし、総費用曲線(TC)がカーブを描いているため、上の計算方法では求めることが出来ません。そこで登場するのが微分です。
微分は、グラフを細かな点と考えて「その点の接線の傾き」を求めることが出来る計算方法です。
- 「利潤(π)=総収入(TR)-総費用(TC)」を微分すれば、それぞれの傾きが得られます
微分すると…「総収入曲線(TR)の傾き-総費用曲線(TC)の傾き」となります。
改めてですが、それぞれ限界収入・限界費用ともなります
・総収入曲線(TR)の傾き=限界収入(MR)
・総費用曲線(TC)の傾き=限界費用(MC)
・総収入曲線(TR)の傾き=限界収入(MR)
・総費用曲線(TC)の傾き=限界費用(MC)
ポイント
ここで、利潤最大化が実現するポイントでは「総収入曲線(TR)の傾き=総費用曲線(TC)の傾き」だったため「総収入曲線(TR)の傾き-総費用曲線(TC)の傾き=0」となります。
重要
まとめると、計算問題では「利潤(π)=総収入(TR)-総費用(MC)」を微分して「=0」とすれば、利潤(π)を最大化した状態になる。

北国宗太郎
長かったけど、利潤最大化で微分が登場するまで分かった。
ここまで理解出来れば、あとは計算問題に対応するだけ!

牛さん
利潤最大化問題を解けるように、次は、実際の文字式で考えられるようにしましょう。
②数式で考える
- 利潤=π
- 価格=P
- 生産量=Y
- 労働量=L
- 賃金=w
- 資本量=K
- レンタル料=r
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
したがって「利潤(π)=(PY)-(wL+rK)」と考える。この数式を利潤関数(π)と呼ぶ。
※「価格(P)」は商品の販売価格(P)・「生産量(Y)」は作ったものを全部売ると考えて生産量=販売量と考えます。なので、販売量(Y)に販売価格(P)を掛けて収入額を計算していることになります。
- 「利潤(π)=(PY)-(wL+rK)」の利潤を最大化させるために微分して「=0」とする
微分して「=0」にすると利潤が最大化する理由を戻って確認する
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
総収入(TR)と総費用(TC)にあたる点線部分を微分していきます。
このとき、重要なポイントが2つあります。
1つ目
- ここで注目するのは「労働量(L)・資本量(K)」です
総費用に関して、賃料・レンタル料は市場によって決められるので、企業は操作できません。そのため、商品・サービスの生産量に応じて変化するのは「労働量(L)・資本量(K)」だけになります(L・K=変数)。
ポイント
つまり、この労働量(L)・資本量(K)が変化すると「どれくらい費用が変わるか=総費用曲線(TC)の傾き」を計算することになります。
そこで、この2つの労働量(L)・資本量(K)のそれぞれで微分するわけです。
2つ目
- 生産量(Y)は、通常「労働量(L)・資本量(K)」によって決まる
「生産関数=Y(L,K)」のように、生産量(Y)は労働量(L)・資本量(K)で決まります。
完全競争市場では、販売価格(P)は市場によって決められるので、企業は操作できません。また、企業は「労働量(L)・資本量(K)」の投入量を変化させて、商品・サービスの生産量をコントロールするため、収入額に影響を与えるのは実質的に「労働量(L)・資本量(K)」です(L・K=変数)。
ポイント
つまり、労働量(L)・資本量(K)が変化すると「どれくらい生産量(収入)が変わるか=総収入曲線(TR)の傾き」を計算することになります
そこで、労働量(L)・資本量(K)をそれぞれで微分すれば、総収入曲線(TR)の傾きも求めることが出来ます。
本来ならば「利潤(π)=(PY)-(wL+rK)」を生産量(Y)で微分して「=0」とすることで、利潤最大化を求めることが出来ます。なぜなら、収入も費用も生産量に応じて変化するためです。例えば、生産量を1増やしたとき、収入がいくら増加したか・費用がいくら増加したかが、それぞれ「傾き」になります。
しかし「利潤(π)=(PY)-(wL+rK)」を微分する時は、一般的に労働量(L)・資本量(K)で偏微分して「=0」と出来ます。なぜなら、収入も費用も生産量に応じて変化しますが、この生産量(Y)は、労働量(L)・資本量(K)によって決まるからです。

北国宗太郎
とりあえず労働量(L)・資本量(K)で微分すればOKだよ。

牛さん
実際に微分をしてみましょう!
- 「∂π/∂L」「∂π/∂K」は、利潤関数(π)をL・Kで微分したことを表しています。
- 「∂Y/∂L」「∂Y/∂K」は、生産関数(Y)をL・Kで微分したことを表しています。
「利潤(π)」も「生産量(Y)」も、実際の数字が入っているわけではないので、このような表記で「微分をした」ということを表現しています。
(wL+rK)の部分は、この時点で実際に計算が可能なので、計算しています。
例えば「L」で偏微分すると‥

北国宗太郎
微分の計算方法は、上に書いている通りだから練習して覚えよう!

牛さん
教科書や参考書によっては、生産量(Y)の部分を「小さなL」「小さなK」としている場合もあります。また、生産量をYではなく「F」「f」「f(L,K)」等としている場合もあります。
表記が違いますが、それぞれ同じことを書いているので混乱しないようにしましょう。
この2つの式を「利潤最大化条件(1階条件)」と言います。

北国宗太郎
牛さん「価格(P)=限界費用(MC)」とは違うの‥?

牛さん
「w/∂Y/∂L」「r/∂Y/∂K」の部分が限界費用(MC)です
イメージが湧きづらいと思いますので「生産関数(Y)=L」の場合を考えます。
「生産関数(Y)=L」というのは、労働1単位で商品を1単位作れる状態です。
すると「利潤(π)=(PY)-(wL+rK)」は「利潤(π)=(PL)-(wL+rK)」となります。
ここで「賃金(w)」は労働1単位あたりの金額です。つまり、右辺は、労働を1単位増やした時の費用の増加分となり限界費用(MC)と同じです。
先ほど「w/∂Y/∂L」「r/∂Y/∂K」の部分が限界費用(MC)と言いましたが、実際に「生産関数(Y)=L」などの関数を使うとイメージできます。
この2つの式が利潤最大化条件(1階条件)となります。
また、完全競争市場の利潤最大化条件として有名な「価格(P)=限界費用(MC)」は、この数式を変形すると求められるものです。

北国宗太郎

牛さん
ここまで理解出来れば、あとは実際の問題を解いていくことが重要です。
最後に大学でミクロ経済学を学習している人向けに「限界生産力(MP)」「生産要素価格」「限界生産物価値」との関係を紹介します。少し混乱するかもしれないので、不要な人は飛ばして大丈夫です。
限界生産力・要素価格との関係
生産関数(Y)をL・Kで微分した「∂Y/∂L」「∂Y/∂K」に注目します。
実はこの部分、限界生産力(MP)を表しています
なので、利潤最大化条件を次のように表記することがあります。
以上のように、利潤最大化条件(1階条件)を
- 労働の限界生産力(MPL)=w/P
- 資本の限界生産力(MPK)=r/P
と表記することもあります。

北国宗太郎

牛さん
「限界生産物価値」と「要素価格」
限界生産物価値
限界生産力(MP)と価格(P)を掛けたものを「限界生産物価値」と言います。
なので、利潤最大化条件を次のように表記することがあります。
以上のように、利潤最大化条件(1階条件)を
- 労働の限界生産物価値=w
- 資本の限界生産物価値=r
と表記することもあります。
賃金(w)・資本のレンタル料(r)を要素価格と言います。そのため「限界生産物価値が要素価格と等しくなる時に、利潤が最大化する」と言葉で表現することもあります。
このように、数式を変形した形で利潤最大化条件(1階条件)とすることがあるので、頭の片隅にでも入れておきましょう。
求め方・計算方法
利潤最大化問題の形式は大きく2つあります。
- 費用関数(C)から求める
- 生産関数(Y)から求める
費用関数(C)は、総費用・平均費用・平均可変費用などから、利潤最大化を求めるものが多いです。
生産関数(Y)は、労働のみ(資本は固定・短期生産関数)・生産要素が2つ(長期生産関数)で考えるものがあります。
それぞれの例題を解いて、イメージを掴みましょう。
費用関数(C)から求める
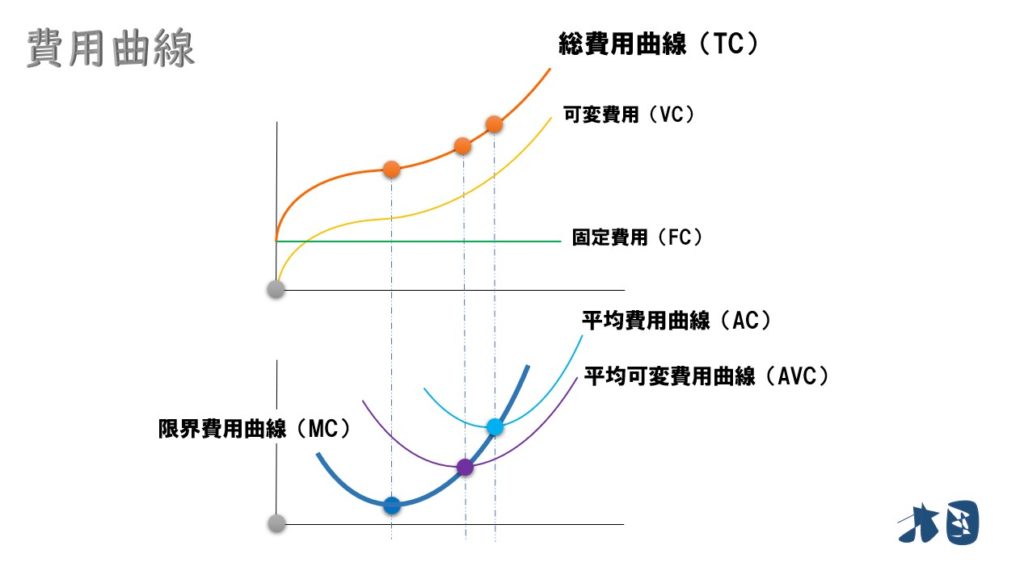
総費用関数(TC)から求める
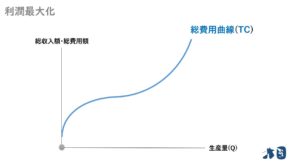
次の費用関数(C)と価格(P)が与えらえれているとき、完全競争市場において企業の利潤が最大化する最適生産量を求める。※Qは生産量を表す
- 価格(P)=21
ポイント
完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使う。
- 価格(P)=21と与えられているため、まずは限界費用(MC)を求める。
費用関数(C)を生産量(Q)で微分すれば限界費用になる
こちらの「限界費用曲線」の項目で総費用との関係性を知りましょう⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界 ※特に「接線の傾き」がポイント
「価格(P)=限界費用(MC)」としてQを求める
・
① 左辺の21を右辺へ移行する
・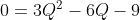
② 両辺を3で割る
・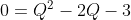
③ 因数分解を行う
・0=(Q-3)(Q+1)
「Q=3,-1」となりますが、生産量はマイナスにならないので「利潤が最大化する生産量(Q)は3」が答えとなる。
平均可変費用関数(AVC)から求める

次の平均可変費用関数(AVC)と価格(P)が与えらえれているとき、完全競争市場において企業の利潤が最大化する最適生産量を求める。※Qは生産量を表す
- 価格(P)=21
ポイント
① 平均可変費用関数(AVC)から総費用関数(TC)を求める。
② 総費用関数(TC)から限界費用関数(MC)を求める。
③ 完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使う。
- まずは平均可変費用(AVC)から総費用(TC)を求める。
平均可変費用(AVC)は生産量(Q)を掛けて固定費用(FC)を足すと総費用になる
「AVC=(TC-FC)/Q」なので、Qを掛けてFCを足せば総費用を求められる。
最後に固定費用(FC)を足すと総費用になります
- この総費用(TC)から限界費用(MC)を求める。
総費用関数(TC)を生産量(Q)で微分すれば限界費用になる
以下「C=~」として計算していきます。
こちらの「限界費用曲線」の項目で総費用との関係性を知りましょう⇒【費用曲線の要点を分かりやすく】総費用・固定・可変・平均可変・限界 ※特に「接線の傾き」がポイント
これで限界費用が求まりました。あとは完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使って、最適な生産量を求めます。
「価格(P)=限界費用(MC)」としてQを求める
・
問題文から「価格(P)=21」となっていたことに注意
① 左辺の21を右辺へ移行する
・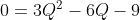
② 両辺を3で割る
・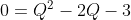
③ 因数分解を行う
・0=(Q-3)(Q+1)
「Q=3,-1」となりますが、生産量はマイナスにならないので「利潤が最大化する生産量(Q)は3」が答えとなる。
生産関数(Y)から求める
生産要素が1つ(労働のみ・短期生産関数)
いま、ある企業の生産関数(短期生産関数)が「Y=√L」と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・労働の投入量(労働需要量・L)を求める。なお固定費用は考えないものとする。
- 価格(P)=4800
- 賃金(w)=1200
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)
したがって「利潤(π)=(PY)-(wL)」と考える。
※「価格(P)」は商品の販売価格(P)・「生産量(Y)」は作ったものを全部売ると考えて生産量=販売量と考えます。なので、販売量(Y)に販売価格(P)を掛けて収入額を計算していることになります。
- 字数を減らしたいので「利潤(π)=(PY)-(wL)」のY(もしくはL)を消す
ここではYを消す場合を考える
「Y=√L」より
- 利潤(π)=(PY)-(wL)
- 利潤(π)=(P√L)-(wL)
⇒「利潤(π)=(P√L)-(wL)」とする。
- 「利潤(π)=(P√L)-(wL)」で利潤を最大化させるには?
上記の式を生産量で微分して「=0」とすれば、利潤が最大化したことになる。
「利潤(π)=(P√L)-(wL)」を生産量で微分します。
ここで、当初の「生産量=Y」は「L」の文字を使って置き換えたので、「生産量(L)」として考えます。したがって「L」で微分して「=0」と置きます。
数式で考えると「Δπ/ΔL=0」←Δπ/ΔLは微分したことを表しています。
「√(ルート)」は「2分の1乗」
そのため「√L=Lの2分の1乗」となります。
微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
「乗数がマイナス」のときは「分数になる」
「利潤(π)=(P√L)-(wL)」を「L」で微分すると‥
- (P√L)は上で説明した通りで微分できます。
- (wL)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
生産量で微分して「=0」としているので、上記の式が利潤最大化が実現している状態となっている。
あとは問題で与えられた「P=4800」「w=1200」を代入して「L」の値を求めればOK!
このままでは計算しづらいので、値を代入する前に変形します。
- 「-w」を右辺へ移行する
- 両辺を「P」で割ります
ここで「P=4800・w=1200」を代入します。
- 両辺を2乗する
利潤が最大化する生産量と労働投入量は‥
- 生産量(Y)=2
- 労働の投入量(L)=4
生産関数が「Y=√L」と与えられていたため「√L=2」を代入すれば生産量(Y)が得られる。
別解
- 完全競争市場における利潤最大化条件「価格(P)=限界費用(MC)」を使う
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)
したがって「利潤(π)=(PY)-(wL)」と考える。
⇒重要なのは「総費用=賃金(w)×労働量(L)」←コレ
ポイント
限界費用(MC)を求めるには、総費用(TC)を生産量で微分すれば求められる。
- 「総費用=賃金(w)×労働量(L)」を生産量(Y)で微分すればOK
ここで、生産量(Y)で微分できるように、労働量(L)を”Y”を使って表す。生産関数「Y=√L」が問題文で与えられていたので、両辺を2乗して「Yの2乗=L」が得られる。
以上より
- 総費用=賃金(w)×(Yの2乗)となる。
これを生産量(Y)で微分すれば‥「限界費用(MC)=2wY」
利潤最大化条件の「P=MC」より「P=2wY」として計算します。
問題文から「P=4800」「w=1200」と与えられていたので
- 4800=2・1200・Y
- 4800=2400Y
- Y=2
また、生産関数「Y=√L」より「2=√L」となるので「L=4」
利潤最大化が実現する最適な生産量は「Y=2」で、労働投入量は「L=4」となる。
生産要素が2つ(通常・長期生産関数)

いま、ある企業の生産関数(長期生産関数)が
と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・各生産要素の最適な投入量(L・K)を求める。
- 価格(P)=2400
- 賃金(w)=1200
- 資本のレンタル料(r)=2400
ここで、与えられた生産関数の乗数が足して1にならないことを確認してください。「Lの0.5乗」「Kの0.5乗」などのように「0.5+0.5=1」となっていると規模に関する収穫が一定となり計算過程が異なります。最後の章を確認してください。
ポイント
「利潤(π)=総収入ー総費用」なので
- 総収入=価格(P)×生産量(Y)
- 総費用=賃金(w)×労働量(L)+レンタル料(r)×資本量(K)
したがって「利潤(π)=(PY)-(wL+rK)」と考える。
※「価格(P)」は商品の販売価格(P)・「生産量(Y)」は作ったものを全部売ると考えて生産量=販売量と考えます。なので、販売量(Y)に販売価格(P)を掛けて収入額を計算していることになります。
- 字数を減らしたいので「利潤(π)=(PY)-(wL+rK)」のY(もしくはL・K)を消す
ここではYを消す場合を考える
- 利潤(π)=(PY)-(wL+rK)
- 利潤(π)=(P・L^0.25・√K)-(wL+rK)
⇒「利潤(π)=(P・L^0.25・√K)-(wL+rK)」とする。
- 「利潤(π)=(P・L^0.25・√K)-(wL+rK)」で利潤を最大化させるには?
上記の式を生産量で微分して「=0」とすれば、利潤が最大化したことになる。
「利潤(π)=(P・L^0.25・√K)-(wL+rK)」を生産量で微分します。
ここで、当初の「生産量=Y」は「L・K」の文字を使って置き換えたので、「生産量(L・K)」として考えます。したがって「L」「K」で偏微分して「=0」と置きます。
数式だと「∂π/∂L=0,∂π/∂K=0」←∂π/∂L・∂π/∂Kは偏微分したことを表しています。
「√(ルート)」は「2分の1乗」
そのため「√K=Kの2分の1乗」となります。以下「√K=Kの2分の1乗(0.5乗)」と表記します。
偏微分をするときは
- 乗数を手前に持ってくる
- 乗数を「1」マイナスする
※0.25=1/4
「乗数がマイナス」のときは「分数になる」
「利潤(π)=(P・L^0.25・K^0.5)-(wL+rK)」を「L」で偏微分すると‥
- (P・L^0.25・K^0.5)は上で説明した通りで微分できます。
- (wL+rK)は(Lの1乗)なので微分すると(1×Lの0乗)=1になります。よって「w×1=w」
「L」で偏微分するなら「L」という文字がついていない部分は無視されます。※あくまで微分は変化量(Lという数量が変化したら式の答えがどう変化するか?)を見るため。
生産量で微分して「=0」としているので、上記の2つの式が利潤最大化が実現している状態となっている。
あとは問題で与えられた「P=2400・w=1200・K=2400」を代入して「L・K」の値を求めればOK!
このままでは計算しづらいので、値を代入する前に変形します。
- 「-w」「-r」を右辺へ移行する
- 両辺を「P」で割ります
ここで「P=2400・w=1200・r=2400」を代入します。
両辺を4乗する
「16Lの3乗」と「L/16」がイコール
計算途中で登場した「L=16Kの2乗」へ代入
生産関数「Y=L^0.25・√K」へ答えを代入
計算していく
- 利潤が最大化する生産量(Y)は「1/8」
- 最適な労働の投入量(L)は「1/16」
- 最適な資本の投入量(K)は「1/16」

いま、ある企業の生産関数(長期生産関数)が
- Y=√L・√K
と与えられているとき、完全競争市場において、この企業が利潤最大化する生産量(Y)・各生産要素の最適な投入量(L・K)を求める。
- 価格(P)=2400
- 賃金(w)=1200
- 資本のレンタル料(r)=4800
ここで、与えられた生産関数の乗数が足して1になるため収穫が一定となります。※「√L=Lの0.5乗」「√K=Kの0.5乗」⇒「0.5+0.5=1」となっている
ポイント
収穫が一定の場合は、費用最小化を求める。利潤最大化するときは、最も効率的な生産が実現しているはずなので、費用が最小化していると考える。
※収穫が一定の場合は特殊な答えになるため利潤最大化条件を使って計算することが出来ません。
- 「(w/r)」=「MPL/MPK」が成立
「生産要素の価格比(要素価格比)=2つの限界生産力の比」
費用最小化についてはこちら⇒【費用最小化】考え方・条件式・求め方について分かりやすく解説
というわけで、まず「労働の限界生産力(MPL)」「資本の限界生産力(MPK)」を求めます
限界生産力(MP)を求める時は微分をしますが、微分する理由が分からない人は「限界生産力・限界生産力逓減の法則」で確認してください。
- 「Y=√L・√K」を「L・K」で微分します
※「√L=Lの0.5乗(1/2乗)」「√K=Kの0.5乗(1/2乗)」
労働(L)で微分する
資本(K)で微分する
ここで、費用最小化が実現するとき、下記の式が成り立つ
- 「(w/r)」=「MPL/MPK」が成立
「生産要素の価格比(要素価格比)=2つの限界生産力の比」
費用最小化についてはこちら⇒【費用最小化】考え方・条件式・求め方について分かりやすく解説
- 「MPL/MPK」を求める
- 「(w/r)」=「MPL/MPK」より
- Y=√L・√K へ代入
- 費用(C)=wL+rK
「L=2Y」「K=(1/2)Y」を費用関数(C)へ代入する
C=w2Y+r(1/2)Y
C=1200・2Y+4800・(1/2)Y
C=2400Y+2400Y
C=4800Y
C=2400Y+2400Y
C=4800Y
この「4800Y」に注目します。
この部分は生産量(Y)を1増やすと、費用が4800かかることを表しています。つまり、費用が4800で一定のため、販売価格(P)の大きさ次第で利潤が出るかが変わります。
- 販売価格(P)が4800より大きい場合(P>4800)
収穫が一定のため、無限に利潤を生み出すことが出来ます。つまり、利潤が最大化する生産量は定まらない(=無限)になります。
- 販売価格(P)が4800より小さい場合(P<4800)
商品を売るたびに赤字になります。そのため、利潤が最大化する生産量は0(=生産しない)になります。
問題文で「価格(P)=2400」とあったので、利潤が最大化する生産量は0となります。
★
経済学では、分析したい対象の財以外の、全ての財を合成した財=貨幣所得と捉え、
このような合成財をニュメレールといい、その価格は1に基準化することが多い。
そして公共経済学の分野では、準線形効用関数(分析の対象となる財の、需要の所得効果が0)という仮定が、
かなり頻繁に用いられる。結構クリティカルな割には、ちゃんと説明している教科書が少ない。
もし準線形選好を仮定しない場合、
コースの定理:
権利をどちらに配分しても、資源配分は同じ(結果は同じ)・・・ではなくなる。
交渉の結果は相変わらずパレート効率的ではあるが、権利の配分次第でパレート効率的水準(資源配分)は
不変でなくなる。
公共財:
サミュエルソン条件は相変わらずパレート効率的ではあるが、公共財の最適供給量が一意に決まらない。
ピボタル・メカニズム(クラーク=グローブス・メカニズム):
そもそも成立しない。
個人的には大問題だと思うんだが、経済学者でこのことをちゃんと強調して語っている人っているのだろうか?
所得を人質にされて、欲しくも無い公共財に賛成票を投じざるを得ない人達のドキュメントとか見てるとね・・・。
● 目次
・「林正義 吉田浩 財政学をつかむ 有斐閣 2008/06」の6章、医療・介護と育児・教育
・「常木淳 公共経済学 新世社 第2版 2002/03」
・「ハル・R・ヴァリアン 入門ミクロ経済学 勁草書房 第9版 2015/08」
・「林正義 小川光 別所俊一郎 公共経済学 有斐閣 2010/12」
・「柴田弘文 柴田愛子 公共経済学 東洋経済新報社 1988/12」
・「板谷淳一 佐野博之 コア・テキスト公共経済学 新世社 2013/01」
・コースの定理
・林公共の10章と12章
● 「林正義 吉田浩 財政学をつかむ 有斐閣 2008/06」の6章、医療・介護と育児・教育
教科書内では、unitという単位で区分されていて、unit23が医療・介護、
unit24が育児・教育となっている。
まず医療保険の公的供給の根拠について。
病気のほとんどに言えることだが、早期発見・早期治療。その方がかえって費用負担も小さいことを踏まえた上で、
1:価値財。
2:感染や公衆衛生などの外部性。
3:所得再分配政策として、現金給付ではなく現物給付。
医療そのものの供給に関する公的関与の根拠。
1:医療従事者に求められる一定の知識・技術の水準は非常に高いので、人的資本への投資に掛かる費用も大きい。
教育への公的関与にも言えることだが、後で賃金所得によって回収できるとしても、
資本市場が不完全だと過少供給になりやすい。
2:入院施設や医療機器などの施設・設備は初期費用が高い。固定費用が小さくなく、費用逓減産業。
3:医療だけではなく、サービス産業全般に言えることだが、貯蔵・運搬が難しいので、地域的偏在が起きる。
子供に対する需要を経済学的に考察。
1:子供がいるということ自体に効用を感じるという意味で、消費財としての子供需要。
消費財(ニュメレール)=c、子供の数=n、1人当たり子育ての費用=pとすると、
効用関数:U(c,n) 、 予算制約:y=c+pn
食事や衣類、保育園や幼稚園、塾や習い事といった教育費が高くなれば、子供に対する需要は低下する。
2:子育てにかかる時間という機会費用。
時間全体=H、1人当たり子育て時間=h*、労働供給に割ける時間=h、賃金率=wとすると、
時間制約:H=h*+h
予算制約:y=wh=w(H-h*)=c+pn → wH=c+pn-w・h*
賃金率wが上昇すると、子育てに使う時間の機会費用が大きくなる。
3:老後の生活を賄うための、投資財としての子供需要。
医療・介護、年金などの保険やサービス(介護サービス事業など)は、
公的供給だけではなく、民間の供給も増えているので、市場サービスの代替としての子供需要は減りつつある。
4:労働力としての子供。
産業構造が農業中心だった時代では、なるべく多人数で共同で行うのが効率的。
実際に農繁期などは学校を休みとして働き手として期待された時期も存在した。
農業自体が機械化されたり、産業構造全体でも農業部門が縮小してきたので、子供需要も減少。
教育に対する公的関与の根拠。
まず数字的には、日本の教育に対する公的な支出水準は、
初等・中等教育まではOECD各国の平均レベルだが、高等教育になるとその平均を大幅に下回ることで有名。
1:一番有名なのが人的資本論。
これに対して、教育には人的資本を増やす効果は無いという意見も存在する。
高学歴な者ほど高賃金というのは、ゲーム理論や情報の経済学的に言えば、
シグナリング(大卒などの資格を取る)や、企業によるスクリーニング(入社試験や面接)の結果であって、
元々高い能力の人が、学歴によってその能力を顕在化させているに過ぎないとのこと。
義務教育までの基礎教育は生産性を上昇させるが、その影響を除いた上で、
高等教育については、その部分だけで純粋に個人の生産性を向上させることは確認されてない
という研究結果も報告されている。
2:外部性。
人的資本の蓄積による成果が、個人の収入に反映されるならば、教育にかかる費用は、
個人の将来においてすべて回収可能ということになる。
しかし、仮にそうであっても、外部性がある場合には過少となる。
一緒に仕事をする場合、相手の能力が高いほど、自分の成果も高まる。
逆も言える以上、お互いの能力が高いほど、生産性は飛躍的に向上する。
3:機会の均等化という公平性と、不完全な資本市場。
単に資本市場が不完全なだけではなく、もう1点重要なのが、教育支出の意思決定は未成年時になされること。
その際、親の資金力(収入)が教育の需要量を決定してしまう。
(親の収入が低い家庭では、親に迷惑をかけたくないという孝行心から、進学を諦める子供もいる。)
ただし、教育サービスの供給者に公的な支出が望ましいとは限らない。
不完全な資本市場が問題なら、教育費をただ引き下げるのではなく(それだと金持ちの子も恩恵を受ける)、
資金を必要とする人への奨学金制度の充実という方向もある。
教育の供給者ではなく需要者に支援という意味では、教育バウチャーなどもある。
教育バウチャーに関する実証研究をまとめた論文としては、次の赤林英夫の論文が面白かった。
http://web.econ.keio.ac.jp/staff/hakab/whatisvoucher20061116.pdf
人気校の周辺の土地は金持ちが買って地価が高くなり、結局貧乏人は人気校に行けないなどの懸念もあるみたいだが、
低所得者だけ補助金を出す方法もあるようだ。
学力向上に有意・有意でないのどちらの実証もあって結論が出ていないようだ。
それよりも本論文で解説される視点は目からウロコ。私立学校というのは受験を通して生徒を選択できる。
しかし教育バウチャーによって私立を含めて生徒側が学校を選択できるようになれば、
私立学校は生徒を選択できなくなるという意味でトレードオフであり、
結果、教育バウチャーは私立の公立化を意味する。
● 「常木淳 公共経済学 新世社 第2版 2002/03」
7章2節、効用関数を同一と見なせるかどうかにおけるラーナーの議論が重要で、
柴田公共ではP224~P227で説明される。
林公共のP278~P280にも、同質の効用関数に関する議論があり、
特にP280の「第2」は、ラーナーの議論に相当する。
ベンサム型とロールズ型の説明については、板谷公共の3章5節~8節(p79~p97)も参照。
○ 7章1節、社会的公平とは。社会的厚生関数と原初状態と無知のヴェール。
社会的厚生関数と社会的無差別曲線の違いは、前者が多数の人々の効用関数で構成される関数なのに対し、
後者はそれを2人に絞ることで2次元の無差別曲線図として図示したもの。
縦軸および横軸は、2人の効用水準を取る。
一方、国際貿易論では生産可能性曲線(PPF)と、1国全体の無差別曲線として社会的無差別曲線が登場するが、
横軸にX財、縦軸にY財をとった2次元のグラフで、社会的厚生関数とは関係ない。
社会的厚生関数は財平面ではなく、個人間の効用平面に描かれ、
個人間の効用水準の「配分」の望ましさを考えるのが目的。
功利主義的社会的厚生関数(ベンサム=ピグー型社会的厚生関数)
効用関数は各個人において同一で、かつ、測定・比較・加算が可能で(効用関数を足し算するので基数的)、
社会全体の効用の和を最大化(最大多数の最大幸福)
W=Σui 1≦i≦n ・・・B
このような社会的厚生関数に理論的な根拠を与える方法として、ハーサニーによる原初的無知のヴェールがある。
各人の社会的位置に関する代替的な選択肢が存在するときに(色々な立場・状態の人がいるときに)、
それらの各位置で当人が得る効用の評価が各人共通であるという仮定を立て、
(つまり同一の効用関数を仮定。その理論的根拠については後述。)
かつ、社会の構成員は自分がどのような社会的位置にあるかまったく不確実であるために
それらすべての可能性を「等確率」と仮定。
A、B、C、Dの4人世界の場合、いったん原初状態に立ち返り(その時に無知のヴェールを通り抜ける)、
そこから各人とも4人の中のどの状態・立場の人間として生まれるかは、
無知のヴェールによって1/4の確率ずつと考える。
すると各人(個人個人)がこのような条件下で獲得する効用の期待値は、
すべての可能な社会的位置で、各人が獲得する効用を(つまり全員の効用を)
足し合わせたもの(に等確率を乗じたもの)になる。
しかも各状態での効用評価は各人共通と仮定しているので、
(各人が原初状態で計算した)効用の期待値は各人共通となる。
かくしてB式に基づく社会的決定を行うということは、原初状態と無知のヴェールの下で、
各人が不確実性下での「危険中立的」な最適化行動に基づく、合意可能な価値判断となる。
つまり期待効用理論において、期待値だけを考慮したリスク中立型の効用関数(線形)となる。
横軸にu1、縦軸にu2を取ると、功利主義の下では、u1+u2の合計Wが同一の値ならば、
各状態は等確率なので結局は期待値も同一となる。
同一の社会的厚生をもたらす効用配分の集合である社会的無差別曲線は、右下がり(45度)の直線となる。
u2=-u1+W ・・・B’
ロールズ型社会的厚生関数はマキシミン原理に従う。原初状態と無知のヴェールの仮定の下での最適化行動として、
一番不幸な人の効用を、最も改善させるのが合理的であると考える。従って社会的無差別曲線はL字型となる。
効用が最低の人だけを考慮するので、効用関数が比較可能であればよく、基数的じゃなく序数的であって構わない。
序数的なら「同一の(重要)」増加関数による単調変換で、社会的順序(その中で最低の人)は不変だから。
ハーサニとロールズがともに依拠した原初状態と無知のヴェールの仮定は、次のように理解できる。
社会的に公平な判断を各自が行うための自然な発想として、
メンバー全員が自分の立場・状態をひとまず括弧に入れてみることだ。
自分の能力や財産などをいったん無視し、各人が他人の様々な境遇を、自分にも降りかかる可能性のあった問題として
真剣に考えることが、公平について考えるときの思考実験として「公正」と言える。
同一の効用関数、原初状態と無知のヴェールの仮定によって、ベンサム型も、ロールズ型も、
社会的無差別曲線は原点から右上がりの45度線を軸に左右対称となる。
ベンサム型だと、完全に効用は互換可能である。
裕福な人の効用が1単位増えれば、貧乏な人の効用が1単位減っても社会的厚生関数上、無差別となる。
社会全体の効用の総和しか論じないので、極端な話、誰か1人が富を独占している状態も許容される。
ロールズ型だと、トレードオフは不可能である。
ロールズ型の問題点としては、効用が最低の人だけを考慮し、それ以外の人をまったく考慮しないこと。
例えば家計1から家計3まで3人いたとして、
所得分配A:(300,500,500)
所得分配B:(290,1000,1000)
マキシミンの原理に従うロールズ型だと、所得分配Aの方が厚生が高くなる。
各家計がリスク回避的だとしても、まったく一切リスクを取らないというのも非現実的である。
要求するリスクプレミアムを超えるならば、不確実な状態を選択する場合だってあるだろう。
ベンサム型とロールズ型の間を取るような社会的厚生関数の例として、ナッシュ型の社会的厚生関数があり、
ナッシュ型の社会的無差別曲線は、
W=u1・u2 → u2=W/u1 ・・・C
効用の積で表現されるので、u1-u2平面(効用平面)でのグラフは、反比例(非線形)となる。

原点から右上がりの45度線との交点付近では、効用は交換が可能だが、
45度線から離れるにつれて、より裕福な人の効用を増やすために、
減らさなければならない貧しい人の効用は小さくなるとする(限界代替率が逓減)。
不平等度が著しく高い場合には、ほとんどロールズ型に近くなり、交換不可能となる。
このような社会的厚生関数は、より貧しい状態の効用を、裕福な状態の効用よりも高く評価するという意味において、
危険回避的な最適化行動をしていると考えられる。
ちなみに社会的無差別曲線を図示する時に描かれるのは、
純粋交換経済で考える場合には効用可能性曲線(UPC:utilty possibility curve)、
生産経済で考える場合には、効用可能性フロンティア(UPF:utilty possibility frontier)。
生産に関しては生産可能性曲線=生産可能性フロンティア(PPF)なので注意。
生産経済を考える場合は、PPF上を移動するに従って、
その内部に形成されるエッジワースのボックスダイアグラムが、いくつもできる。
従って効用可能性曲線もその度にできるので、効用可能性曲線群の包絡線が、効用可能性フロンティア。
○ 7.2節、ラーナーの議論。効用関数の同一性について、さらに原初状態と無知のヴェールの仮定を用いてみる。

P188の図7.2より、もし限界効用が逓減するなら、限界効用が均等化する(所得)分配Aが、
u1+u2=効用和(グラフの下側の面積OaCbO’)を最大にする。
(限界効用が逓減することを前提にしているので、効用関数はリスク回避型である。
ちなみに「配分」と「分配」の使い分けは、「資源は配分」、「所得は分配」。)
ラーナーによると、効用関数の同一性に関しても、原初状態と無知のヴェールによって根拠を与えられる。
効用享受能力もまた、原初状態における社会的位置の可能な選択肢、構成要素の1つと考えられるからだ。
図7.2では、効用関数が違うaとbの限界効用曲線(どちらも所得に対して減少関数)が描かれている。
左の原点Oからaの所得、右の原点O’からbの所得を取り、縦軸に限界効用を取る。
aの方が効用享受能力が高い場合、aの限界効用曲線の方が位置が高い。
すると、aとbの限界効用曲線の交点は、真ん中より右側に位置する。
限界効用が均等化している交点をC、そのときの所得をA点とし、両者の所得合計のちょうど半分の所をB点としよう。
そこでA点から所得の再分配によりB点にしたとすると、三角形CDEの厚生損失が発生する。
しかし効用享受能力も、原初状態と無知のヴェールによって、お互い真逆の効用関数だった可能性を考慮してみよう。
効用関数の位置関係(左からの限界効用曲線の方が位置が高い)はそのままに、aがbに、bがaになりつつ、
元々の所得分配を考察するには、B点を軸にA点と対称な点A’を、出発点に考えなければいけない。
A’点から出発して、所得の再分配によりB点にしたとすると、発生する厚生の「増加」は、台形GFDEとなる。
これは先ほどの厚生損失の三角形CDEよりも大きい。
たとえ効用享受能力に個人差があっても、2種類の厚生変化が「等確率」で生じる原初状態と無知のヴェールの下では、
台形>三角形であることから、所得再分配によるB点の実現は、期待効用和を純増させる。
結局、このような思考実験により、効用関数の同一性を認めることが可能となる。
● 「ハル・R・ヴァリアン 入門ミクロ経済学 勁草書房 第9版 2015/08」
○ 準線形効用関数(準線形選好)と、ニュメレール(合成財あるいは貨幣所得)
準線形効用関数(準線形選好)については、 ミクロ経済学ノートを参照。
次章の林公共や、最後の方にあるコースの定理を理解する上で、必須の前提条件なので、
先にミクロ経済学ノートを読んでおこう。
一方、分析したい対象の財以外の、全ての財を合成した財=貨幣所得と捉え、
そのような合成財をニュメレールといい、その価格は1に基準化することが多い。
○ 37章、公共財。
2人経済を考え、
・各人の私的財消費量:x1、x2
・各人の富の初期保有量:w1、w2
・各人の公共財に対する費用負担:g1、g2
・各人の公共財に対する留保価格:r1、r2
それぞれの予算制約式は、
x1+g1=w1
x2+g2=w2
公共財の購入に掛かる費用をcとすると、次の制約も満たさなければならない。
g1+g2>c
個人1の効用関数を次のように表記する。
u1(x1,G)
G=公共財で、個人2も同時に等量消費可能。Gは0と1の値を取り、0なら公共財が無い、1なら有る。
留保価格=支払意思額
消費者が買ってもいいと考える上限価格で、購入するか・しないか、が無差別となる価格なので、
u1(w1-r1,1)=u1(w1,0) ・・・1
「もし公共財への支出がパレート改善可能ならば?」
u1(w1,0)<u1(x1,1)
u2(w2,0)<u2(x2,1)
左辺に留保価格の定義1式、右辺に予算制約式を用いると、
u1(w1-r1,1)=u1(w1,0)<u1(x1,1)=u1(w1-g1,1)
u2(w2-r2,1)=u2(w2,0)<u2(x2,1)=u2(w2-g2,1)
効用関数は、xの増加関数なので、不等号をそのまま用いることができて、
w1-r1<w1-g1
w2-r2<w2-g2
よって、パレート改善が可能であるためには、次が必要条件となる。
r1>g1
r2>g2
次のパレート改善の十分条件が満たされれば、両者を改善する支払計画が必ず存在することを意味する。
r1+r2>g1+g2=c ・・・2
・ ここまでの注意点
ここまでは効用関数について準線形選好であることは仮定してない。
従って、一般的に留保価格r1、r2は、富の初期保有量に依存するだろう。
ある富の分配では、r1+r2>cであったものが、別の分配に対しては、r1+r2<cとなることもありえる。
極端な例として、富を独占する1人の富豪と、大多数の貧しい人がいる状況で、
富豪がその公共財に対する選好が強く、留保価格が高ければ、自分で費用を全額負担しようとするだろう。
逆に富豪がその公共財に対して無関心ならば、大多数の貧乏人が必要としていても公共財を購入しないことが
パレート効率的になってしまう。
・ いよいよ準線形効用関数
公共財に対する需要が、所得や富から独立と仮定してみよう。準線形効用関数の定義より、
個人1の準線形効用関数:u(x1,G)=x1+v1(G) ・・・3
このように定式化すると、対象となる財はGであり、それ以外の私的財x1はニュメレールとなる。
単純化のために、v1(0)=v2(0)=0としよう。この場合、留保価格の定義である1式より、
u1(w1-r1,1)=w1-r1+v1(1)=w1+0=u1(w1,0)
u2(w2-r2,1)=w2-r2+v2(1)=w2+0=u2(w2,0)
となり、これより、
r1=v1(1) ・・・4
r2=v2(1) ・・・5
公共財に対する需要が、所得や富から独立であることから、公共財に対する留保価格も所得や富から独立となる。
・ 37章4節、P648~、公共財の最適供給(サミュエルソン条件)
MRS1=個人1における、私的財に対する公共財の限界代替率、dx1/dGとすると、
MRS1+MRS2=MRT(限界変形率=生産可能性曲線(PPF)の傾き)
MRT=相対価格(pG/px1)=MCG/MCx1 ・・・6(利潤最大化条件のP=MCより)
・ 37章5節、P651~、準線形選好と公共財
一般的な公共財の最適供給の問題(サミュエルソン条件)に、準線形選好の仮定を導入してみよう。
私的財xに対する効用は線形で、その限界効用は1である。限界代替率=限界効用の比なので、
MRS1=dx1/dG=MUG/MUx1=MUG=∂u1(x1,G)/∂G ・・・7
個人2についても同様で、結局、限界代替率はGのみに依存する。
そしてサミュエルソン条件より、x1やx2とは無関係に、公共財の最適供給量(効率的水準)は一意に決まる。
2人の間で私的財をどんなに再分配しても、2人の無差別曲線の傾きである限界代替率は変化しないので、
公共財の供給量が効率的水準で一定なままなので、私的財と(供給量一定の)公共財のあらゆる資源配分は、
すべてパレート効率的である。
当たり前っちゃ当たり前である。私的財は関係ないのだから。
誤解しがちなのが、別に準線形選好の仮定が無くても、サミュエルソン条件はパレート効率的である。
ただ、その最適供給量が一意に決まるかどうかが、今問題にしている準線形選好の仮定と関係してるだけ。
・ 37章の6節~8節、P652~、フリーライダーと公共財の供給量の決定問題(特に投票)。
私的財は、消費の外部性がないので、市場で個人個人が分権的に意思決定していれば、
全体的にもパレート効率的になる。
神の見えざる手と言われるが、市場(で決まる価格)自体が、民主主義的な投票システムなのである。
しかし、公共財の場合は外部性(市場で直接取引した者以外にも効果が及ぶ)があるので、
フリーライダーの問題も含めると、個人の意思決定だけでは社会的に最適にならない。
公共選択として最も一般的な意思決定メカニズムは、投票である。
しかし推移性を満たさず(循環しちゃう)、社会的決定が不可能となる
(コンドルセの)投票のパラドックスが発生する。
中位投票者定理によると、公共財の量に対する選好が単峰型ならば、社会的決定はできる。
(あくまで、「決定はできる」という程度。)
直感的に言うと、公共財を望む量が小さい方から順番に並べて、
中位より多い支出を望む人(グループA)と、少ない支出を望む人(グループB)は、
中位の定義により半々となるので均衡する。
中位より少ない支出と中位の人が望む支出を比較した場合、グループAは中位の人が望む支出に投票する。
逆に中位より多い支出と 〃 、グループBは 〃 。
しかし、中位投票者定理によって決まる公共財の供給量は、決定はできるが効率的水準であるとは限らない。
半分の人はその中位となる水準より多い支出を望み、半分の人は少ない支出を望むが、
それが定量的にどれくらいなのかは考慮されていない。また、投票結果を操作しようと、
戦略的に行動(自分の真の選好を表明せずに偽って投票)するインセンティブも生じる。
・ ここだけヴァリアンの入ミク(5版)の35章9節、真の選好を表明させるためのメカニズムデザイン。
まず基本的に、公共財の供給が効率的であるためには、個人iの価値(便益)をvi、公共財の費用をcとすると、
Σvi≧c ・・・8
でなければならない。この時点で、準線形選好の仮定が入っている。
2式の十分条件に、準線形選好の仮定を用いて導出した4式と5式を代入すると、8式が導出される。
デザイン1:受益者負担として、表明した価値に比例して費用を割り当てる(リンダール・メカニズム)。
デザイン1の問題点は、フリーライドしようとして、過少申告するインセンティブが生まれる。
そこで個人iの費用負担を、選好表明の前に決定しておくと、
デザイン2:表明した価値viと、分担費用ciが独立。
純価値(純便益)ni=vi-ci ・・・9
後はΣni>0であるかどうかを調べればいい。
しかしデザイン2だと、ni>0の人は、真の価値より過大に申告するインセンティブが生まれる。
過大に申告すればするほど、公共財が供給される可能性が高まるからである。
逆に、ni<0の人は、真の価値より過少に申告するインセンティブが生まれる。
・ ピボタル・メカニズム(クラーク=グローブス・メカニズム)
「奥野正寛 ミクロ経済学 東京大学出版会 2008/04」の7章10節(p340~最後)
奥野ミクロの正誤表、図表集、双対性の詳しい説明が次のサイトにある。
https://sites.google.com/site/okunomicroeconomics/textbook/figures_and_tables
かなりの教科書を読んできたけど、クラーク・メカニズムの説明に関しては、本書が一番簡潔で上手い。
やっぱ図解って素晴らしい。
さて、クラーク=グローブス・メカニズムの成立にも、前提条件として3式の準線形効用関数を仮定する。
そして個人iの費用負担Tiを次のように設計する。
限界変形率=私的財で測った公共財供給の限界費用=c (教科書ではp329に記載)
私的財はニュメレール財と仮定しているので、その価格は1に基準化。
利潤最大化条件のP=MCより、私的財の限界費用も1となる。
その私的財をc単位投入することで、公共財を1単位作れることを意味する(6式を参照)。
cは公共財1単位の(相対)価格でもある。
Ti=cG-Σvj ただしΣの範囲はj≠i、すなわちi以外の全員 ・・・10
もし2人経済だったなら、
T1=cG-v2 ・・・11(教科書では7.11式)
このように設計しておくと、自分の費用負担は、政府に申告する自分の効用(公共財に対する)とは
関係が無くなるため、虚偽報告するインセンティブが無くなり、真の価値を表明するようになる。
その理由を以下の図7.8を用いて説明しよう。

・縦軸は限界効用vi'(G) (vi'(G)>0、vi''(G)<0とする(図では直線になっているけど))
・原点同士の距離=線分O1O2の長さ=c(これ重要1)
まず個人2がv2(G)#を表明しているとしよう。v2(G)#は真の効用関数とは限らない。
このとき、個人1が真の効用関数v1(G)を表明すれば、公共財供給量はG0となるので、重要1より、
総費用cG=四角形O1G0DO2の面積 ・・・12
図7.8に描かれているv2'(G)#は、個人2の限界効用関数であり、準線形選好の仮定の下では、
ミクロ経済学ノートの、 10式より需要曲線でもある。
限界関数と横軸との間の面積が総関数(限界関数を積分すると総関数)なので、
v2(G)#=四角形O2DEFの面積 ・・・13
11式を踏まえると、個人1の費用負担額は、
T1=四角形O1G0EFの面積 ・・・14
となる。一方、個人1の需要曲線はv1'(G)なので、個人1の消費者余剰は三角形FEIとなる。
これに対して、個人1が効用関数をv1(G)#として虚偽申告すると、公共財供給量はG#、
虚偽申告していても真の限界効用関数はv1'(G)なので、12~14式の要領で個人1の消費者余剰を計算すると、
四角形FE'JIになる。
虚偽申告すれば三角形EE'Jの死荷重損失が発生する。Bもまったく同じことが言えるので、
真の効用関数を報告することが、支配戦略均衡になる(相手の戦略に関係ないので)。
均衡点Eでは、v1'(G)+v2'(G)=cが成立しており、6式のサミュエルソン条件も成立している。
ただし、クラーク=グローブス・メカニズムには、1つ重大な問題がある。
14式では個人1の費用負担額T1を導出した。
一方、個人2の費用負担額T2の導出にあたっては、個人1の限界効用関数(需要曲線)v1'(G)を用いるので、
T1=O1G0EF ・・・15
T2=O2DEI ・・・16
総費用cGは12式なので、三角形FEIの赤字が必ず発生してしまう。
● 「林正義 小川光 別所俊一郎 公共経済学 有斐閣 2010/12」
まず最初に、公共経済学の中でも、特に外部性や公共財を理解するにあたっての注意点。
外部性と公共財は、それぞれ別のちゃんとした定義がある。どちらも市場の失敗。
外部性(外部効果)は、取引してる同士「以外」の人、まさしく「市場の外」に効果が及んでしまうこと。
良い効果は外部経済、悪い効果は外部不経済。
公共財は、非競合性(使ってもなくならない)、非排除性(使おうとしている人を排除できない)、
という基準で定義される財。従って発生する問題が、フリーライダー問題。
しかし外部性のある財や公共財を議論するときには、最終的には本質的に同じ構造となる。
外部経済を他者から受け取ることも、外部不経済を他者に与えることも、
どちらも外部効果に対してフリーライドしているのと同じだからである。
その性質のため、個人Aと個人Bにとって等量消費となる。
外部性や公共財の性質から、市場での取引以外の経路で、他者の行動(需要量・供給量)が自分にも影響を与える。
逆に自分も他者に影響を与える。となると、相手の行動を考慮した上で、自分の行動を決定しなければならない。
そのような意思決定を、戦略的意思決定といい、お互いがそのような関係にあることを、戦略的相互依存関係という。
(完全競争市場での意思決定は、自分についてだけであり、消費にしろ生産にしろプライステイカー。)
そこで説明によく出てくるのが非協力ゲーム(囚人のジレンマ)の構造。
相手の戦略を所与(与件)として、こちらの最適反応戦略を求めるという考え方と、
お互いの最適反応戦略同士の均衡点(グラフで言えば交点)が、ナッシュ均衡であるという定義の理解は必須。
民間同士の自発的な行動や市場にまかせておくと、落ち着き先であるナッシュ均衡は、
決してパレート効率的ではない状態となるが、その状態とパレート改善方法(すなわち政府の必要性)が
まさに公共経済学で扱う対象となる。
上記のような問題と、その定式化でおなじみなのが、クールノーモデルである。
市場需要全体が制約条件として入ってきて、それを少数のプレイヤーで奪い合うという構造がクールノーモデル。
市場需要全体に対して、自分の最適な生産量q1を決める際には、相手の生産量q2も自分の問題の中に入ってくる。
その相手の生産量q2を所与(いったん定数)として、自分の最適生産量を求めると、
求まった最適反応関数は、q1とq2の関数となり(q2は変数に戻る)、q1-q2平面にグラフを描ける。
そしてお互いの最適反応関数をq1-q2平面に描いて交点を求めると、それがナッシュ均衡なのである。
(交点を求めるということは、最適反応関数同士を連立させて解く。同時に最適解が成り立つということ。
「戦略的」という単語を見かけたら、このように相手の行動が自分の問題の中に入ってきて、
その相手の行動をいったん所与(定数)として最適化問題を解くと、機械的に覚えておけばいい。
自分のことだけ考えればいいのではなく、相手のことも考えて自分の行動を決定する。)
市場需要を奪い合うように、制約のある資源を奪い合うという意味では共有地の悲劇も同様である。
その数式的な構造は、クールノーモデルと同じであることが、
「中山幹夫 はじめてのゲーム理論 有斐閣 1997/09」の3章3節に書かれている。
中山はじめては、全部読まなくていいが、3章3節だけは図書館などで絶対先に読んでおこう。
ゲーム理論ノートにも引用した。
後、結構出てくるのが、1次同次の生産関数でのオイラーの定理(完全分配定理)。
すなわち、規模に関して収穫一定の場合、利潤は常に0であり、生産物(収入)は生産要素に分配され尽くす。
経済数学ノートの 「21:オイラーの定理」を参照。
さて、いよいよ林の公共経済学に入るが、4章外部性、5章公共財では、
柴田の扇形ダイアグラムを使って説明している。
一般的な消費財の一般均衡の図で有名なエッジワースのボックスダイアグラムに対して、
柴田のダイアグラムは外部性や公共財を図解できて、とても理解しやすくて超便利。
考案したのは次の章で紹介する柴田だが、本書の林公共の方が簡潔に説明していてわかりやすい。
さらに嬉しいことに、次のWEBサイトで、林先生の講義ノートが公開されている。
https://sites.google.com/site/publicfinanceuoftokyo/toppage/public-finance-law
いつ無くなるか分からないので、積極的に図を引用して残しておこうと思う。
林公共の教科書の方の4章と5章と柴田のダイアグラムについては、講義ノートではファイル07になるが、
教科書と同じ図はあるものの、説明文がないのでやはり教科書を読む必要がある。
○ 4章、外部性
教科書のP123より、柴田のダイアグラムが扇形と呼ばれる理由は、
外部性を引き起こす財(5章なら公共財)の、価格(=限界費用)が逓増する場合、
ダイアグラムが扇形になるから。
4章と5章では、価格(=限界費用)は一定と仮定するため、ダイアグラムは直角三角形になる。

Z:外部性のある財(5章の公共財では記号がG)。
個人Aと個人BのZの消費量、ZA=ZB=Z(公共財の場合、GA=GB=G、どちらも等量消費)。
X:ZやG以外のすべての私的財(合成財とかニュメレールといい、価格は1に基準化)。
OBから見ると、上に向かってBの私的財Xの消費量(=XB)。
OAから見ると、下に向かってAの私的財Xの消費量(=XA)。
MAおよびMB(個人の所得)、MA+MB=M(図には無いが、M=総所得)。
ZやGの価格p(=限界費用)は一定で、私的財Xをニュメレールとしていることから、
pはそのまま私的財に対する相対価格にもなる。
1単位のX財を、p単位のZ財に作り変えることができる。従って、OAZmaxの線は経済全体の制約線となる。
右斜め下に伸びる、OAZmaxの線:X=M-pZ
例えばAがZ0を購入し、BはMBを全額X財で消費したとしよう(とはいえ、BもZ0を等量消費せざるを得ない)。
D点から出発して、左にZ財を1単位動かすと、上にp単位移動する。
AのZ財の消費金額は、pZ0円になり、残りのCDの距離がAのX財の消費量XAになる。
すなわち、任意のZ0に対する経済全体のX財の総消費量は、Z0からOAZmax線までの垂直距離
 _
_
図4-6の上のa図は、普通の無差別曲線の図。等量消費となるZ(以下、Zバー)からEまでの距離が、
AのX財の消費量となる(E点ではXもZもどちらも最適消費量)。
図4-6の下のb図は、柴田のダイアグラムの図で、Aの無差別曲線の記号は、VAとする。
VAは、下方に位置するほど効用が高い。
E点からZバーまでの距離=斜めのOAZmax線から、真下に向かってF点までの距離(AのX財消費量)で、
図4-5で言えば、CDの距離。
すなわち、HJ線=個人Aの予算制約線(これ大事)
a図とb図は、三角形の面積は同じまま、原点のOAが上下逆転している。

図4-7は、Bにとっての無差別曲線の図で、外部効果を発生させる方をAとしているので、
Bにとって外部経済のときは通常の右下がりだが、外部不経済になると、無差別曲線は右上がりとなる。
Bの無差別曲線の記号はIBとし、柴田のダイアグラムにはそのまま描く。
外部不経済の場合、IBは左上に位置するほど効用が高い。

図4-8は、AとBの無差別曲線を柴田のダイアグラムに描き、両者が接する点の軌跡=契約曲線KK’となる。
外部不経済(タバコ)を例に取り、Aが喫煙者、Bが被害者とする。
Aに喫煙権があると、Bのことを気にせず吸ってしまうので、Aにとってのタバコの最適消費量F点が決まる。
Bは強制的に等量消費せざるを得ないので、F点を通る無差別曲線IBバーになる。
しかしB自身はタバコZを買ってはいないので、MBを全額Xの消費に充てている(Fの高さ=OBHの距離)。
ただし、注意点!!!図4-8と次の図4-9には、誤植がある。次のサポートウェブに、正誤表がある。
http://yuhikaku-nibu.txt-nifty.com/blog/2010/10/post-d373.html
いつかサイトが無くなったときのために引用しておくと、縦軸のOAHの線分について、MB=誤、MA=正。
Bの所得MBは、OBHの距離である。
F点より左下にできるレンズ内部は、両者にとって効用が高くなるので、パレート改善できる。
逆に言えば、外部性が発生している(ピグー税によって内部化されていない)状態では、パレート非効率的となる。
レンズ内部の、さらに契約曲線κκ’の部分を、ミクロ経済学では「コア」という。
コアとなっているZの消費量は、Zバーよりも少ないので、裏を返せば、Zバーは過剰消費である。

図4-9は、外部経済の例で、例えばAが花壇を購入したとしよう。
隣に住んでいるBにとっても嬉しいことなので、IBは右下がりだが、Bは花壇を購入していないので、
MBを全額Xの消費に充てている(Fの高さ=OBHの距離)。
レンズは右下にできているので、Zバーは過少消費となっている。

図4-10で、もしBに綺麗な空気を吸う権利がある場合は、Aは所得を全額、私的財の消費に使うしかないので、
強制的にH点を通る無差別曲線になる。
○ (公共財の)需要の所得効果がゼロの仮定(=準線形効用関数の仮定)
準線形効用関数(準線形選好)については、 ミクロ経済学ノートを参照。
この仮定を置くと、例えば図4-8の契約曲線KK’は、横軸上のZバーの水準で垂直になり、
最適な水準(量)は一意(ユニーク)に決まる。
教科書ではその話はP130~P131で触れられていて、
5章の公共財の方でも同じ話があり、P148の図5-2と文章が該当する。
詳しくは章末の練習問題4-4に回されていて、上記のサポートウェブに解答がある。
いつかサイトが無くなったときのために、解答を引用しておくと、
「Zの需要に所得効果が存在しない場合,任意の値にZが固定されている限り,
Xの値がどのように変化しようが,限界代替率(無差別曲線の傾き)は変化しない。
ある配分で両者の無差別曲線の傾きが等しければ,その配分で与えられるZの値では,
Xがどのような値をとろうとも,両者の無差別曲線は等しくなる。
つまり,無差別曲線の傾きが等しくなる配分は横軸で測られた,そのZの値から伸びた垂線と等しくなる。」
本ノートの後ろの方に書いているコースの定理の章で詳しく述べるが、
図4-10については、契約曲線KK’が垂直でないために、
権利の配分次第で、効率的な資源配分の水準が変化する。
Aに喫煙権がある場合は、Z3~Z4の範囲、
Bに綺麗な空気を吸う権利がある場合は、Z1~Z2の範囲が、効率的な資源配分の水準となる。
どちらもパレート効率的ではあるが、資源配分の水準自体は、権利配分の仕方で変化している。
コースの定理によれば、どのように権利配分しても、民間同士の自発的な交渉(取引)によって、
政府が何をしなくても、勝手にレンズ内のコアのどこか(=パレート効率性)は実現し、
かつ、(所得分配の結果には影響を与えるが)資源配分は「不変」であるはずだった。
しかし、取引費用がゼロで交渉可能であっても、上記のように、Zの需要の所得弾力性が0じゃない限り、
もはやコースの定理は成立しない。準線形選好の仮定が必要なのである。

図4-11は、ピグー税やピグー補助(定額じゃなくて定率じゃないとダメ)が課されると、
予算制約線の傾きが変化する。
ピグー税の場合、Aから徴収された税は、全額Bに所得移転されることにも注意。
Aに補助金を与える場合には、Bから徴収することになる。
外部不経済のある財Zにピグー税だとS’に、外部経済でピグー補助金だとS’’になるから、
柴田のダイアグラムで、個人Aの予算制約線は、前者だとHJ’に、後者だとHJ’’になる。
外部性については、取引費用が0ならば、ピグー課税やピグー補助金を用いなくても、
当事者同士の交渉によって自発的にパレート効率的な資源配分は実現する。
しかし取引費用が大きく、交渉が不可能なケースについては、次の図4-12のように、
上手くピグー税やピグー補助金によって、外部性を内部化させてやらないと、パレート改善できない。

これまでの話は、喫煙家のAと、嫌煙家のBの2人だった。嫌煙家がBとCの2人に増えた場合、どうなるだろうか?
もしBがAにお金を払って喫煙量(排煙量)を減らしてもらった場合、Cはそれにフリーライドできる。
お互いフリーライドしようとした結果、交渉によるパレート効率的水準はもはや実現しない。
パレート非効率的な状態がナッシュ均衡となってしまう。
権利を確定するだけではダメで、そのような状況は公共財と同じとなる。
公共財は自発的にパレート効率性を実現するのは不可能なので、政府が必要になる。それを次で説明しよう。
○ 5章、公共財
・ 5章3節、公共財の自発的供給(拠出均衡)
個人Aの自発的な公共財の供給量(拠出量)をgA、個人BのそれをgBとすると、
公共財の供給量:gA+gB=G → gA=G-gB ・・・5.4
個人Aの予算制約:xA+pgA=MA → xA+pG=MA+pgB ・・・5.3
ファイル07のP32は、教科書とはちょっと記号が違う。
ファイル07では、5.3式のpgBの部分を、pg-Aと表記している。
以下、教科書の方の記号で説明する。
さて、5.3式で注意すべきは、Bの公共財供給量(拠出量)gBに応じて、Aの予算制約が変化すること。
AやBにとっての5.3式は、それぞれの個人所得(MAやMB)と区別して、完全所得と呼ぶ。

図5-3の上側は、一般的な無差別曲線の図で、予算制約線のうちMAQ3の水平線より上の破線部分は、
Bによって拠出された公共財を消費するしかないので、Aにとっては選択できない(私的財を消費できない)。
私的財も公共財も上級財(正常財)ではあるが、Bが公共財を拠出し続けてくれて、
AにとってQ3まで行ってしまうと、AはMAのすべてを私的財の消費に使ってしまい、
それ以上は私的財の消費は増やせない。
図5-3の下側は、例えば横軸上でG3点では、斜めのOAG線から、q3点がある水平線までの垂直距離が、
Aの私的財の消費量xAとなる。
その時のAの完全所得は、MA+pgB3であり、上の図より個人所得MAは、私的財xAの消費で使い切っており、
公共財の総供給量はG3(=gB3)となっている。

図5-4で、MBの高さにある水平線で、gA3という記号になっているのは、
Aの拠出金はpgAで、それがBにとっての縦軸上での予算制約線のシフト幅になるのだが、
予算制約線そのものは-pの傾きなので、pgAをpで割れば、横軸の変化となるためだ。
(y=-pxからy=-px+pzと縦軸切片が変化すれば、y=-p(x-z)と横軸切片はzになる。)
図5-3のq0~q3と、図5-4のE0~E3は、それぞれAとBの所得-消費曲線となる。
両者の図を合わせれば、図5-5となる。

図5-4のE3からE4への水平移動は、もうすでにBにとっての個人所得MBは、
全額私的財の消費に使ってしまっているので、それ以上Aが公共財への拠出を増やしてくれても、
その増やしてくれた分は、そのまま公共財の消費に用いるしかないためだ。
q3やE3までは、相手の公共財拠出の増加に伴うこちらの予算拡大によって、
私的財も公共財も上級財なので、両財とも消費を増やす。
予算拡大とは言っても、個人所得はそのままなので、それなのに私的財の消費を増やしているということは、
相手の公共財の拠出増加に対して、こちらの拠出は少し減らしていることを意味する。
この辺の説明は、「土居丈朗 入門公共経済学 日本評論社 2002/11」
2章3節、P31の図2-5と、P32-P33の文章がまさにピッタリなので、そちらで説明しよう。

予算制約線:xA=-pG+MA+pgB ・・・5.3
予算制約線の角度がpということは、横軸で1単位動けば、縦軸でp単位動くことを意味する。
MAF=pgB → MAI=gB=OJ
線分OF:Aの完全所得
Bの拠出金(負担金)pgBを所与として、Aは最適消費水準Eを決定する。
線分OK:Aの欲する最適な公共財の総供給量G
線分JK:gA
さて、MAとpは不変として、gBが増えたとしよう。
Aにとって実質所得の増加に等しく、予算制約線は右上にシフトする。
私的財も公共財も上級財なので、新しい均衡点E’は図2-5Bのようになる。

予算制約線:xA=-pG+MA+pgB’ ・・・5.3’
MAF’=pgB’ → gB’=OJ’
gBの増加分=JJ’
線分OF’:Aの完全所得
線分OK’:新しくAの欲する最適な公共財の総供給量G
線分J’K’:gA’
予算制約線のシフト幅=FF’=Aにとって実質所得の増加分
に対してE’点では、その全額を公共財の消費には充てていない。
私的財も上級財なので、私的財の消費量も増やしている。
MAが不変の中、xAを増やせば、その分だけAの拠出量は減り、gAからgA’に、JKからJ’K’になる。
図2-5から類推すれば、逆にBが公共財供給量を減らせば、Aにとっての実質所得の減少となり、
私的財の消費量を減らしつつ、Aの拠出金pgAは、逆に若干増えることになる。
このような現象や効果は、他の学問でも文章だけで説明されたりしているのかもしれないが、
無差別曲線を使った図解は、ミクロ経済学の真骨頂だと思う。
林公共に戻ろう。図5-5では、お互いの所得-消費曲線の交点(S点)が、自発的供給(拠出均衡)となる。
拠出均衡はナッシュ均衡ではあるが、パレート効率的ではない。
S点より右下のレンズは無差別曲線同士で作られ、S点からその内部への移動はパレート改善となる。
外部性とは違って、公共財の場合、お互いがフリーライドしようとするので、
交渉によってパレート効率性が実現(コースの定理)することはない。ナッシュ均衡なので自分からは動かない。
S点は、必ずパレート非効率的となる。なぜなら、S点でのお互いの無差別曲線の傾きを考えると、
VAの傾きは必ず0(水平)であり、IBの傾きは必ず-pだからである。
・ 中立定理(必ず成立するとは限らない=重要)

図5-6、拠出均衡(S点)の状態から出発して、BからAへと所得移転(⊿M)を行っても、
拠出均衡点はS点のままで不変となる。それを中立定理という。
AとBの効用関数自体が変化しない限り、Aの個人所得の予算制約線(JH→J’H’)も、
Bの個人所得の予算制約線((JC→J’C’)も、その傾きは等しいままなので、
それぞれの所得-消費曲線は、始点が変わるだけとなる。
Aの所得-消費曲線の始点は、q0→q0’に、
Bの所得-消費曲線の始点は、E0→E0’に、なるだけ。
ワーの中立命題(P.G.Warr 1983)とも言われる。土居公共の2章4節(3節ではないことに注意)や、
井堀利宏 財政 (現代経済学入門) 岩波書店 などにも載っている。土居公共の2章4節の方が詳しい。
公共財は等量消費可能なのでGの水準は不変だが、費用負担の拠出は変化する。
(従って、拠出均衡が不変という言い方は、誤解を招くような気がする。確かに均衡点Sは不変だが。)
BからAへ所得再分配が行われれば、Bはその分だけ公共財への(拠出金)を減らすが、
逆にAが増加させて相殺する。結果、公共財の総供給量Gは変化しない。
例えばAで言えば、斜めのOAZmax線から、拠出均衡のS点までの距離は不変なので、私的財消費量は不変。
しかしBから所得移転⊿Mを受けているので、拠出金pgAを増やしていることになる。
pgAの増加量は、他方で同じロジックでBが減らしているであろうpgBの量となる。
図5-3の下の図と、図5-6を併せて見れば分かるように、
中央の水平線(J’H’)から最適消費点までの距離が、Bの拠出金pgBだからである。
そして、拠出均衡のS点は不変なので、無差別曲線も移動していないので、効用水準も変化しない。
ちなみに中立定理(中立命題)は、次の文献によると、
Warr(1983)より以前に、Sibata(1971)で暗黙のうちに導出されていたとのこと。
「フィナンシャル・レビュー / 財務省財務総合政策研究所 編 75号 2005年
井堀 利宏 国際公共財の供給と各国の経済厚生」
上記の文献および、上記の井堀財政にも載っていて面白いのが、トランスファー・パラドックス。
日本、アメリカ、ドイツ、それぞれの防衛費に関して自発的供給のナッシュ均衡になっているとしよう。
アメリカ:全世界の防衛費に興味。
日本:アメリカと日本(太平洋)だけに興味。
ドイツ:アメリカとドイツ(大西洋)だけに興味。
アメリカの防衛費=純粋公共財、日本とドイツのそれぞれの防衛費=準公共財。
「交易条件は一定」として、日本からアメリカへ所得移転(トランスファー)が起きると、
日本は防衛費を減らし、アメリカは防衛費を増やす。両国だけを見れば私的財の消費量を含めて経済厚生は不変。
ところが、アメリカの防衛費の増加は、ドイツにとって経済厚生を高める。
ドイツにとっての公共財の総供給量Gの増加は、ドイツの実質所得の増加となる。
その結果、ドイツは私的財の消費量を増やし、防衛費を減らす(上記の土居公共の2章3節の分析が該当)。
結局、ドイツがフリーライドするわけだが、これはアメリカの経済厚生を低下させる。
ドイツが拠出を減らすので、アメリカにとって実質的な所得の低下となり、私的財の消費を減らしつつ、
ドイツが減らした分の「一部」を埋め合わせるように、アメリカはさらに防衛費を増やす
(これも上記の土居公共の2章3節の分析が該当)。
この副次的なアメリカの防衛費の増加は、日本の経済厚生を高める。
そうすると、日本がアメリカに所得移転してあげた立場なのに、
アメリカの経済厚生は低下し、逆に日本の経済厚生は高まる結果となる。
「交易条件は一定」としたが、この交易条件効果を考慮すると、国際貿易論の話となる。
トランスファー問題と言われ、有名なのがケインズと(ヘクシャー=オリーン・モデルの)オリーンの論争。
さて、林公共に戻ろう。中立定理は必ず成立するとは限らない。
所得移転(⊿M)によって、個人Aの当初の予算制約線JH(個人Bの当初の予算制約線はJC)が、
J’H’へと(個人BのはJ’C’へと)下方シフトするが、当初の拠出均衡点Sより下に来てしまうと、
拠出均衡はS’点になってしまう。それを示すのが次の図5-7。

図5-6で言えば、図の中央にある水平線から拠出均衡点までの垂直距離が、Bの拠出金であるpgBとなるので、
所得移転(⊿M)によって予算制約線が下方シフトすれば、その分だけpgBが自動的に減る。
ところが、拠出均衡点を越えて予算制約線が下方シフトしてしまうと、pgBがマイナスとなってしまう。
井堀財政でも、中立命題が成立しない理由が文章だけで説明されており、
公共財の負担量が負になりえないとのこと(非負制約)。
所得再分配をやり過ぎて、最初の拠出均衡の水準に対する費用支払いができないほど、
Bの所得が無いという意味では、所得制約(予算制約)とも言える。
ちなみに、中立定理が成り立つにしろ、成り立たないにしろ、どちらも需要の所得効果の話とは関係ない。
そもそも拠出均衡の点Sや点S’はパレート非効率的で、
どちらもパレート効率的な水準となる契約曲線上(図5-5のKK’曲線)とは違う所にある。
そのとき(違う所にあるとき)、契約曲線が垂直であるかどうかとは関係ない。
・ 5章4節、拠出均衡とクラウディングアウト。
まず、すでに拠出均衡が成立していて、ある程度の公共財をすでに自発的に供給している状態から出発する。
その状態から、政府による課税と、その租税収入を原資とした公共財の供給を政府が直接行うと、
その分だけ民間による自発的な公共財供給が減少し、完全にクラウディングアウトする(均衡点はSのまま)。
その際の重要な仮定が、図5-6の所得移転と同じ効果となるように、課税方法を「定額税」とすること。
「定率税」だと、予算制約線の傾きそのものが変わってしまう。
このクラウディングアウトに関しては、教科書の方では文章による説明だけしか無いが、
講義ノートの方では、ファイル07のP39~P42で、定式化と図解が行われている。
いつ無くなるかわからないので、ここもノートを取っておこう。
AとBからの徴税:TAとTB
政府による公共財供給(実質):gG
政府の予算制約:pgG=TA+TB → gG=(TA+TB)/p
5.3式と5.4式(公共財の供給量:gA+gB=G)より、
課税前の個人Aと個人Bのそれぞれの予算制約式は、
個人Aの予算制約:xA+pgA=MA → xA+pG=MA+pgB
個人Bの予算制約:xB+pgB=MB → xB+pG=MB+pgA
それぞれの予算制約式にTAとTBを課税すると、



図5-6の中立定理と同様に、AとBの所得-消費曲線の始点が変わるだけで、拠出均衡点Sは不変である。
ただし、クラウディングアウトが発生しないケースも考えられる。
章末の練習問題5-4で、解答は上記サポートウェブ。それによると、答えは図5-7の事例である。
図5-7では、Bは公共財を供給していない。
JJ’’に相当する所得移転(⊿M)をAは受けており、自分の所得-消費曲線に従って、
最適な公共財の量(S’)をすでに自発的に供給している。
Bに公共財を供給してもらって(gB)、Aの実質所得が増加している形ではなく、
Bから所得移転を受けて、Aが自身で拠出していることになる。
一方、Bの最適消費点はS’なので、Bにとって最適な公共財の消費量は、
すでにAが供給している公共財の総量で十分賄えている。
ちなみに、図5-7のS’点は、図5-4で言えばE4点に相当する。
そのBに課税しても、Bが公共財の供給を減らすことはない(そもそも供給してないから)。
さらにAの所得-消費曲線は右下がりなので、最終的に公共財の総供給量は増えている(公共財も上級財だから)。
というのも、A自身が政府の人間だったとしよう。
実質的には所得移転と同じだが、名目上はMAは不変だし、かと言ってBから徴収した税を、
MAとして勘定してしまうと、さすがに横領となるw
勘定はしないが、A個人としての公共財供給gAは減らして、私的財の消費(は上級財なので)に充てれば、
Bから徴収した税があるので、それを当てにして、政府による供給を加えた公共財の総供給量を
最適消費として増やすのが、Aにとって最適。
クラウディングアウトしている話に戻そう。
マクロ経済学的な発想で、クラウディングアウトは悪いというイメージがあるが、
上記の話はそれだけでは個人的に問題だとは思えない。民間投資をクラウディングアウトしているわけじゃないし。
結局AとBが社会契約を結んで、「政府」という肩書きを作っただけで同じ公共財を供給しているだけの話だし、
どちらにしろ拠出均衡(S点)自体がパレート効率的ではない。
S点から右下のレンズ内に移動するように政府が公共財を供給でき(社会契約を結べ)れば、パレート改善である。
では、そのパレート効率的な公共財の水準を、実際に政府が供給できるのかどうか、そのメカニズムが問題となる。
上記のように、所得のみに影響を与える「定額税」だと、政府による公共財の供給はパレート改善できない。
公共財の価格に影響を与える「定率税」が必要となる。人頭税のような定額の固定税だと、上手く行かないのである。
そこで同じ5章4節のクラウディングアウトの続きとして、P162より、リンダール・メカニズムの話となる。
ちなみに、地方交付金のような政府間財政移転だと話は逆となり、歳出とは独立の定額が望ましい。
その話題については、講義ノートのファイル10を参照。歳出に比例するような「定率」の交付(ピグー補助)は、
地方公共財のスピルオーバーなどの外部性があるときには望ましい。
・ 5章4節の続き、リンダール・メカニズム。
リンダール・メカニズムは、公共財の需要量に応じて負担率tが決まる受益者負担のメカニズムである。
AとBの2人経済ならば、tと1-tになる。あるtの値の下で需要を表明させて、
両者の需要量が一致するまでtの値を変えては表明を繰り返す。
一致すれば、パレート効率的となるサミュエルソン条件も成立する。
またtの値が決まれば、AとBがそれぞれ直面する公共財価格は差別価格となる。
私的財(ニュメレール)をX、公共財の(相対)価格をp、所得をMとすると、
Aの予算制約式:Xa+tpG=Ma
Bの予算制約式:Xb+(1-t)pG=Mb
公共財の限界費用を一定として、負担率×限界費用=tpはAが直面する租税価格といい、
リンダール均衡が成立したときの租税価格をリンダール価格という。
次にAとBにとっての効用最大化条件(相対価格=限界代替率)は、
A:tp=MRSa(Xa,G)=MRSa(Ma-tpG,G)
B:(1-t)p=MRSb(Xb,G)=MRSb(Mb-tpG,G)
最終的に公共財の需要量が等しくなれば、公共財は等量消費可能なので、G*=Ga=Gbであり、
tp+(1-t)p=pである以上、左辺の1項目にAの最適化条件式、2項目にBの最適化条件式を代入すると、
MRSa(Ma-tpG*,G*)+MRSb(Mb-tpG*,G*)=p ・・・サミュエルソン条件
このリンダール・メカニズムも、柴田のダイアグラムで分析できるのが面白い。
(柴田公共では5章のP162~P165。)

図5-9では、まずAの負担率がt=1だった場合、Aの予算制約線はJHのままである。
そこから、負担率が下がれば、図4-11でピグー補助をしてもらってるのと同じになるので、JH’になる。
定率税により価格が変化しているので、価格-消費曲線と言える。
一方、Aの負担率がt=1のとき、Bの負担率は1-t=0なので、負担をしないことを意味する。
Bの予算制約線もJHとなる(重要)。
柴田のダイアグラムにおいてBは、無差別曲線図をそのまま描いていることを思い出そう。
本来なら予算制約線は右下がりだが、BにとってGの価格は0なので、J点の高さで水平となる。
Aの負担率が1から下がれば、Aの最適消費点は、q0からq’に、BはE’’になる。
両者の公共財需要量は一致していない。特にBが多すぎて、Aが少ない。
リンダール・メカニズムに従って、さらにAの負担率tを下げて行くと、
L点で両者の無差別曲線は接していて、リンダール均衡という。
価格調整による均衡が、パレート効率的であるという意味で、準市場的であり、
図5-5の拠出均衡よりもパレート改善していることがわかる。
追記。リンダール・メカニズムでは、負担率(および租税価格)に対して公共財需要量は変化する。
結果的に、AとBは等量消費になり、サミュエルソン条件も成立する。
これは、公共財の最適供給量が一意に決まるための条件として、
公共財需要の所得効果が0であるという条件は必要なのだろうか?
準線形効用関数の場合、所得効果は発生しないので、価格が変化した場合、発生するのは代替効果のみとなるが、
関係があるのだろうか?結論。必要ないし関係ない。
まず準線形効用関数は、「所得」が変化した時に無差別曲線および最適消費点がどのように動くか
についての話であって、リンダール・メカニズムで動いているのは「価格」である。
そしてサミュエルソン条件の成立というのはパレート効率的になるだけの話であって、
別に最適供給量が一意に決まることまで、言ってるわけではない。
逆に言えば、所得分配次第で、任意のパレート効率的資源配分を実現できる。
「厚生経済学の第二基本定理:適切な所得分配(初期保有量の分配)を行えば、
その後は競争均衡によって、任意のパレート効率的資源配分を達成できる。」
次の柴田公共のP154とP168より、リンダール・メカニズムは、第二定理とよく似ているとのこと。
次の次の板谷公共のP135より、問題点として、公共財が下級財のケースでは、
所得が増えて高所得者になった場合、かえって公共財への需要が減るので、負担率が逆に下がってしまうとのこと。
高所得者ほど安全・医療・道路・公園などについて自分で賄えるため、政府が直接供給する公共財については、
低所得者の方が需要が大きくなる。リンダールメカニズムで求める費用負担の割合は、逆進的になる。
○ 5章5節、メカニズムデザイン。6章、内容は公共選択論。
リンダール・メカニズムには、真の需要顕示のインセンティブが無く、虚偽報告する可能があるので、
続いてメカニズム・デザインの話に移る。
クラーク=グローブス・メカニズムや、林公共ではヴァリアン・メカニズムも説明される。
前者については、柴田公共ではよく考えられた数値例で詳しく説明されるが、奥野ミクロの簡潔さも素晴らしい。
6章の公共選択論については、専門書はまだ読んだこと無いが、
公共経済学の教科書の中では、次の柴田公共が個人的にベストだった。
林公共の6章で面白かった、P196~P201の、直接民主制と間接民主制のパラドックスについて、
林の講義ノートの方には無いみたいなので、
オストロゴルスキーのパラドックス(逆説)と、コラム10の漸進的改革vsビッグバン改革の話を、
雑記ノートの方で。
○ 7章、地方分権と政府間財政関係(租税競争)。
・ まずはP213~P215、ヘンリー・ジョージ定理と資本化仮説。
ヘンリー・ジョージ定理:都市人口が最適規模である時、地代と地方公共財の費用が等しくなる。
効用関数U(x,g)で、xは私的財、gは地方公共財。
生産関数f(n,l)で、nは人口、lは土地。土地は固定的な生産要素なので簡単にf(n)とする。
資源制約は、xについては人数分消費されるが、gについては等量消費が可能なので、f(n)=nx+g。
これをg=f(n)-nxとして効用関数に代入。
U(x,f(n)-nx)をnで微分してゼロと置いて最適化条件を導出。その際、合成関数の微分となる。
∂U ∂U ∂g ∂U
───=───・───=───・[f'(n)-x]=0 → 1階の最適化条件式:f'(n)=x
∂n ∂g ∂n ∂g
人口のnで微分しているということは、最適人口を求めていることになる。
そして地方公共財を対象としているので、この最適化条件式は人口移動を前提とした最適人口規模を意味する。
左辺の方が大きければ、生産量の限界的な増加に対して、人口流入に伴う限界的な私的財の消費増加量は小さい。
従って、地域人口を増やすべきとなる。その逆は減らすべきとなる。
一方、生産関数が1次同次ならば、オイラーの定理(完全分配定理)が成り立つ。
すなわち、規模に関して収穫一定の場合、利潤は常に0であり、生産物(収入)は生産要素に分配され尽くす。
経済数学ノートの 「21:オイラーの定理」を参照。
また利潤最大化の条件から、労働の限界生産力=実質賃金(f'(n)=w)。
地代の合計をRとすると、f(n)=nw+Rと分配され尽くすので(省略したが、本来はf(n,l)なので)、
R=f(n)-nw=f(n)-nf'(n)=f(n)-nx=g。
すなわち、R=gとなるが、最適人口規模が達成されている状態では、
結果的に地方公共財の費用と地代は等しいことを意味するだけで、
議論を逆さまにして、地代に100%課税(結局は国有化)すれば、
地方公共財の供給量が自動的に最適になるというわけではない。
資本化仮説:地方公共財の供給増がもたらす限界便益の総和は、すべて地代(つまり地主)に帰着する。
以下は、次のファイルを参考にする。
http://repository.osakafu-u.ac.jp/dspace/bitstream/10466/10434/1/2010900034.pdf
要約を先に述べると、人々の選好が同質、移動が自由、などの一定の条件が成立するとき、
借地・借家・賃貸マンションなどの借り手にとっては、地方公共財の増加に伴い、
人口流入による地価や賃貸料の上昇によって、最終的に効用の純増は起きないからだ。
本ノートの一番最初の「財政学をつかむ」の章で紹介した教育バウチャーの話と似ている。
結局、人気校の周辺の土地は金持ちが買って地価が高くなり、貧乏人は人気校に行けない。
消費財x(ニュメレール)、土地h、地方公共財g、
支払う地代R(xはニュメレールなので、Rは相対価格にもなる)、一括税τ、所得y、
家計(住民)の効用関数と予算制約式は、
_
効用関数:U(x,h,g)=u ・・・1
予算制約式:x+Rh=y-τ ・・・2
_
となる。uは、どの地域においても等しい効用水準で、
逆に言えば、足による投票によって、地域間の効用差が無くなるまで、家計は移動し続けることを意味する。
後は最適化(微分して0と置く)。 _
人口はnで一定、1人当たり土地需要h、土地の供給はHで固定。
_
土地市場での需給均衡条件:nh=H ・・・3
供給曲線が垂直で、土地需要の変化は、すべて地代の変化で吸収される。
裁定条件が成り立つように、地域間の効用差が無くなるまで(裁定機会が無くなるまで)、
地代という価格で調整されるのだろう。
実際に、効用関数を全微分して、dU=0と置けば、無差別曲線の限界代替率が求まるので、
予算制約式の方も全微分して、一定の所得の下なのでdy=0とすると、予算制約式の傾きが求まる。
その他の条件を一定として考えるので、まずは地方公共財の供給増だけの効果を見るために、dτ=0とする。
租税の効果は次のステップで考える。消費財xの限界効用をUxと表現すると、
Ux Ug
Uxdx+Uhdh+Ugdg=0 → dh=-──dx-──dg ・・・A1
Uh Uh
dx+hdR+Rdh=0 → dx=-(hdR+Rdh)・・・A2
限界代替率=予算制約式の傾きなので、A1式とA2式の連立方程式となる。A1式にA2を代入すると、
Ux Ux Ug
(1-──R)dh=──hdR-──dg ・・・A3
Uh Uh Uh
消費財と土地の2財の関係で言えば、x-h平面での家計の効用最大化の1階条件から、
Ux/Uh=Rとなるので、A3式の左辺=0となる。さらに次のような概念と記号を定義すると、
地方公共財の限界的な供給増に対する、地代の増加量=地代勾配=dR/dg=Rg
dR 1 Ug
───=Rg=──・── ・・・4
dg h Ux
3式を代入すると、
Ug _
n・──=Rg・H ・・・5
Ux
地方公共財の限界効用(限界便益)の総和=地代変化の総額
地方公共財を増やしたときに、増える効用の総和が、まるまる地代の増加量で吸収されることになる。
5式の左辺の分母にUxがあるが、ニュメレール(合成財であり、所得とも考えられる)の価格は、
基準化されて1だが、限界効用(Ux)については、準線形効用関数を仮定することによって一定にできる。
ただし上記の結論も、下記に続く結論も、別に準線形効用関数が必要条件というわけではない。
Ug/Uxの部分を、地方公共財の限界効用と表現してるだけ。
上記は、租税の効果を0(dτ=0)としているので、UGは粗限界便益という。
租税負担を考慮しないグロスの限界効用で、考慮すると純限界便益となるので、次のステップに移ろう。
租税効果を考慮して、さらにGの費用関数c(g)を導入し、地方政府の予算制約式、nτ=c(g)も加えると、
サミュエルソン条件が成立することを示そう。
その際に、地方政府は地代が最大になるように地方公共財を供給するとし、地代勾配=dR/dg=0となる。
A1式はそのままだが、改めて家計の予算制約式と、地方政府の予算制約式を全微分すると、
dx+hdR+Rdh=-dτ → dx=-(hdR+Rdh+dτ)・・・A4
dτ c'(g)
ndτ=c'(g)dg → ───=────・・・A6
dg n
まずA4式を、A1式に代入すると、
Ux Ux Ux Ug
(1-──R)dh=──hdR+──dτ-──dg ・・・A7
Uh Uh Uh Uh
相変わらず、家計の効用最大化の1階条件からUx/Uh=Rとなるので、A3式の左辺=0となる。
dR 1 Ug 1 dτ
───=──・──-──・── ・・・A8
dg h Ux h dg
これに3式を代入すると、
_ dR UG dτ
H・───=n・──-n・── ・・・A8
dg Ux dg
さらにA6式を代入し、dR/dg=Rg=0を利用すると、
_
H・Rg=n・(Ug/Ux)-c'(g) → n・(Ug/Ux)=C'(g)
地方公共財の限界効用の総和=限界費用 (サミュエルソン条件)
本来であれば、地方公共財は受益者負担の原則が望ましいが、そうはならないことを示すのが資本化仮説。
地主が人気の地方公共財を望み、ゴミ処理場のような不人気な地方公共財を嫌う理由がよくわかる。
だからと言って、上記の結論だけで勝手に地主を憎んではいけない。
大切なのが実証で、地方公共財の便益が、どの程度地価や家賃に反映されているのか、
資本化を確認して「開発利益の還元」を模索しなければならない。
・ 7章2節、政府間財政関係(租税競争)。
ティブーの足による投票仮説は、政府間の競争(資本や労働力となる住民の獲得)を通じて、
公共財に対する選好の顕示が上手く示されて、市場均衡的にパレート効率性が実現できると考える。
しかし、政府間で企業や工場、優秀な人材を奪い合うために、それらに課される税率は過度に引き下げられる一方、
その地域に固定的な労働や土地などには、過度に税負担が重くなることがよくある。
租税競争と言って、公共財を非効率的な水準に過少供給してしまう可能性がある。
ティブーの足による投票仮説が成立するための詳しい条件については、次の柴田公共のノートで説明。
オーツと言えば地方分権化定理だが、一方で上記のような「底辺への競争」という懸念も示していた。
分権化定理は、公共財の供給量を20望むグループと、40望むグループがいるとき、
画一的に平均値である30を供給すると、両グループとも10の分だけ厚生がマイナスになる。
20と40をそれぞれ供給する地域があった方が望ましいという話。
オーツの懸念をフォーマルに検証する研究が、ウィルソン(J.D.Wilson)らによってなされた。
詳しい分析は、次の次の板谷公共の所で行うので、用語の定義だけ先に。
直接的財政外部性=スピルオーバー。地方公共財の便益が、その他の地域にも及ぶこと。
水平的財政外部性(間接的財政外部性)=
A地方が税率を上げると、B地方へと労働や資本が流れ、Bの税収が増える(外部経済)。
AはBでの外部経済まで考慮せずに税率を上げるので、税率を上げることの費用については
逆に過大に見積もってしまう。結果として、地方政府の設定する税率は過少となる(租税競争)。
垂直的財政外部性=
課税ベースが同じ場合、国税+地方税なので、国が国税を上げちゃうと、地方は何にもしてないのに税収減。
後でもう1度触れるが、同じ課税ベースに対して参入するので、
共有地の悲劇(つまりクールノーモデル)と同じ構造となる。
同じ課税ベースに対して、国と地方の競合に関する話なので、資本や労働が移動することを通じた、
間接的な外部効果ではない。
○ 10章の公的扶助と、12章の年金。
ちょっと長いので、いったんここで区切って、本ノートの最後に回そう。
● 「柴田弘文 柴田愛子 公共経済学 東洋経済新報社 1988/12」
1つ上の林公共の最初で説明したように、林公共の4章外部性、5章公共財で、
柴田のダイアグラムを使って説明しており、林公共の方が簡潔に説明していてわかりやすい。
もし柴田公共を読む予定ならば、先に林公共の4章と5章を読んでおこう。
○ P84~P87の、生産可能曲線(PPF)の非凸性

X財の生産によって公害(工場が川を汚染)が発生し、Y財(農業)に被害が及ぶとしよう。
その場合、そのような外部性が無いときと比べて、生産可能曲線(PPF)は横軸の切片が原点方向にシフトする。
しかし縦軸の切片は、公害を発生させるX財の生産がゼロなので、Y軸の切片は凹まない。
外部性が無いときのPPFの横軸切片をR、外部性によって凹んだときの横軸切片をSとすると、
SR上でもX財は生産可能となる。
その場合、凹んだPPF上で、X財とY財を両方生産するより、
凹む前の外部性が無いかのようなPPF上に位置することになるR点でX財だけを生産した方が、
かえって社会厚生は上昇する。
もうY財は生産されていないので、ある意味外部性が発生しておらず、川を農業用水用に清浄化するより、
工場排水のための下水として使ってしまった方が望ましいということもありえる。
色んな教科書を読んでいると、凸性と内点解を安易に仮定してその話だけで終わることが多いが、
現実には非凸性と端点解(コーナー解)の問題はとても重要。
○ P87~P94、共有地の悲劇
次の板谷公共で、柴田公共の説明も加えて一緒に説明。
○ 非競合性と価格差別(4章および5章)
4章1節のP141より、非排除性のある財は、等量消費せざるを得ないのに対して、
非競合性のある財は、等量消費が「望ましい・すべき」という違いがある。
非競合性のある財は、追加供給に対する限界費用がゼロなので、
価格をゼロにして、お金を払わない消費者も参加させるべきとなる。
4章2節、非排除性がある場合は、フリーライダーが起きる。
自己の需要を顕示し、支払意思を表明しないので、供給も過少供給となる。
では、排除性があれば市場供給量はパレート効率的になるかというと、
排除性があっても競合性が無ければ、やはり過少供給になる。
限界費用がゼロならば、価格もゼロにして消費させればパレート改善するからである。
ミクロ経済学を勉強していると、もはや操業停止点より上の限界費用曲線=供給曲線にしか目が行かないが、
仮に固定費用が賄えない場合、そもそも供給されないという問題が発生してしまう。
一般的に最適化条件である価格=限界費用(P=MC)ばかりが強調されるが、
固定費用の存在および平均費用が逓減している区域が見過ごされがちである。
排除性があり、さらに市場供給が可能であったとしても、非競合性がある場合、
一律の入場料を課して払える人だけに消費させるのは、パレート非効率的である。
そこで差別価格を用いることで、消費者をもっと増やすことができ、パレート改善できる。
するとその財は、排除可能であっても、租税(差別価格)で賄い、あたかも非排除性(と非競合性)のある
公共財として供給することが望ましいことになる。さらに詳しい説明と数値例が、次の5章。
ここから5章。個人的に本書の中で一番好きな章が、5章の準公共財。
クラブ財と地方公共財が有名で、どちらも排除性はあるが競合性はない。
前者だとスポーツクラブの例が有名で、会員制にして排除することは可能だが、
施設内の設備を利用するにあたっては、混雑しない限りは競合性はない。
地方公共財の場合には、地理的に排除性が成立する。
5章2節、平均費用逓減財と非競合性はパラレル。
規模の経済が働くと、利潤最大化の下では独占価格が付けられ、パレート非効率的(過少供給)になる。
さらにP194の下から12行目からの説明が、個人的に目からウロコだった。

独占市場で、限界費用がゼロの場合、M点で供給量が決まり、独占価格はPとなる。
独占企業の収入は、原点Oから始めて□OMLPの長方形となる。
限界費用0なので、そのまま生産者余剰となる。
もし完全競争市場ならば、P=MCより価格は0、総余剰は三角形ODD’となり、
生産者余剰は0なので、総余剰=消費者余剰となる。
独占によって価格はPに上昇し、総余剰はODLMに減少するだけでなく、
総余剰に占める消費者と生産者との分配(割合)も、消費者が不利となり、生産者に有利となる。
さて、もし平均固定費用曲線(AFC)が、L点の下側を通るなら、固定費用を賄える。
ところが、もしAFC’がL点の上側を通るなら、固定費用を賄えないので、そもそも市場に供給できない。

では、このような財は供給すべきではないのだろうか?
この独占企業の総費用は、□OMG’F’の長方形となる(限界費用はゼロなので可変費用もゼロ)。
一方、消費者余剰は、△ODD’というでっかい三角形になる。
もし△ODD’の面積が、□OMG’F’の面積よりも大きいならば、
この財を供給することによって正の社会的余剰が生まれる。
(混雑するまでの)非競合財は、限界費用がゼロである以上、とりあえず全員に無料で提供し、
消費者余剰(パイ)を最大にするパレート効率的水準を実現しておいて、
その中から固定費用を別途徴収すればいい。その徴収方法は最大化された消費者余剰の分配問題に過ぎない。
平均固定費用を消費者から一律に徴収する方法もあるが、その場合、上記のように市場供給されない場合もある。
しかし、4章2節のP145~P147にもあるように、一物一価にする必要は無く、
独占市場でおなじみの価格差別を用いる方法もある。その数値例が5章2節のP195~P198にある。
マイクロバスのチャーター料が2200円で、次の表5-B
| 留保価格 | 費用分担 |消費者余剰|
──────────────────────
A| 550円 | 500円 | 50円 |
B| 500円 | 450円 | 〃 |
C| 400円 | 350円 | 〃 |
D| 350円 | 300円 | 〃 |
E| 300円 | 250円 | 〃 |
F| 250円 | 200円 | 〃 |
G| 200円 | 150円 | 〃 |
──────────────────────
|2550円 |2200円 | 350円|
1人当たり平均費用を一律に課すような価格設定だと、上記の数値例では市場供給されない。
2人で分配=1人当たり1100円
3人で分配= 〃 733円
4人で分配= 〃 550円
5人で分配= 〃 440円
6人で分配= 〃 360円
7人で分配= 〃 314円
しかし、支払意思額である留保価格の合計は、2550円でチャーター料を超えている。
そこで、表5-Bのように費用分担(価格差別)することにより、供給可能(パレート改善)となる。
○ 価格差別の種類
第1種価格差別:1人1人の留保価格を完全に知っているので、1人1人に異なる価格を設定
第2種価格差別: 〃 を完全には知らないので、消費量ごとに異なる価格を設定
第3種価格差別: 〃 を完全には知らないので、グループごとに異なる価格を設定
・ 第1種価格差別(完全価格差別ともいう)
表5-Bは、需要曲線とも考えられる。このケースでは消費者余剰を全て吸収することができる。
面白いのが、このケースではMC曲線より上はすべて生産者余剰となるので、
留保価格=限界費用となる個人まで財の供給が行われ、死荷重損失は発生しない。
個人個人の留保価格を完全に知っているというケースは、現実的にはなかなかあり得ないが、
一番近い例として、僻地の医者がある。
同一の医療サービスに対して、金持ちから多く取り、高価格を提示。貧乏人には逆に低価格を提示。
平均費用価格を一律に提示すると、固定費用が賄えず、医療サービスそのものが提供できなかったのだろう。
負担の不平等は、高負担を課せられた者にとってもパレート改善で効用を高める。
また、独占市場と価格差別の理論における一般的な注意点として、再販不可能な財に限られる。
再販可能であると、価格差を利用して裁定取引が起きるからだ。
逆に言えば、再販可能な非競合性のある財は、たとえ排除可能であったとしても、やはり市場供給は困難となる。
非市場的なコスト負担方法が必要となる。
・ 第2種価格差別
代表的なのが、スーパーなどでの大量購入割引、抱き合わせ、二部料金制。
次の第3種価格差別で説明するように、価格弾力性が大きい人ほど、値段が下がったら消費量を大きく増やすことと、
結果は同じになっているが、仕組みはまったく違う。
第1種や第3種のように、個人やグループで需要曲線(留保価格や価格弾力性)を、企業が識別するのが困難なので、
価格と数量の組み合わせが違うメニューを提示し、消費者に「自己選択」させていることになる。
自己選択メカニズムと来れば、参加制約条件と誘因両立制約条件である。
「ヴァリアンの入ミク(9版)の26章3節、P419~P422」では図解で、
「芦谷政浩 ミクロ経済学 有斐閣 2009、のP245」では数値例で、その説明があるが、
「柳川隆 吉野一郎 ミクロ経済学・入門―ビジネスと政策を読みとく 有斐閣 2008/03」
のP159~P164がオススメで、ノートかコピー必須。
参加制約条件と誘因両立制約条件を、これ程までに簡潔にわかりやすく説明したものは他に無いと思う。
ミクロ経済学ノートにもまとめた。
「抱き合わせ」、ヴァリアンの入ミク(9版)の26章5節、p424~p425。
共通に掛かる費用を削減できる。論文はいくつかまとめてホッチキスで留めて学術雑誌として売られる。
互いに補完財ならば、読む方としても効率が良い。
ワープロソフト 表計算ソフト
個人A 120円 100円
個人B 100円 120円
同じ会社Cが、それぞれのソフトを個別に売ってみよう。単純化のため限界費用は0とする。
ワープロソフトだけを売るなら、価格設定は100円にしないと個人Bまで買ってくれない。
表計算ソフトも同様に100円となる。会社Cの収入は400円となる。
ところが、抱き合わせ(パッケージ)にすることで、パッケージソフトの価格を220円にすれば、
個人Aと個人Bの両者とも買ってくれる。会社Cの収入は440円となる。
「二部料金制」。
まず、図1(MC=0)の場合、価格=限界費用で財をD'まで供給すると、
固定費用OJKD'の分だけ赤字となる。
二部料金制では、限界費用に等しい価格で財を供給しておき、発生する赤字については
基本料金(固定料金)を別途徴収する。
購入量をX、価格をPとすると、
支払い(E)=基本料金(F)+従量料金(PX)
1単位当たり支払は、両辺をXで割ると、
E F
──=──+P
X X
従って、消費者1人1人に対して同じ従量料金を提示するが、消費者にとっては購入量が増えれば増えるほど、
1単位当たり支払った価格は下がる。
二部料金制で有名なのが、電気・電話・ガス・水道などの公共料金や、遊園地(入園料と乗り物料)など。
http://tomoinoue.web.fc2.com/notes/notes.html
より、スポーツジムの数値例を引用。
会員(C)は、1日500円
非会員(N)は、1日1000円
ただし、使用日数をX、年会費6万円とすると、年間支払額Eはそれぞれ、
Ec=500X+60000 → Ec/X=500+(60000/X)
En=1000X → En/X=1000
使用日数1日当たりの支払価格が等しくなるときの、使用日数Xは、
500+(60000/X)=1000 → X=120
年間120日より多く利用する消費者は、会員になった方が得である。
スーパーの大量購入割引も同様で、大量購入した人でないと値引きを受けられない。
逆に価格弾力性の低い人は、値段を下げた所で大量購入してくれないので、
そのような人は元々、多少高かろうが安かろうが、少量しか欲しくないと思っている。
そのような人向けに、バラ売りで少量ずつ買えるけど単価は少し高いメニューが用意されている。
この第2種価格差別にも再販の問題が発生する。消費者間で転売可能だと、誰か1人が「まとめ買い」して、
みんなで分ければ、大量購入割引を受けられたり、基本料金をほとんど支払わなくて済む。
二部料金制では、貧しい人は基本料金を払えないという問題が発生するが、
上記の僻地の医療サービスも同様なのだが、基本的には別問題である。
確かに需要の価格弾力性の違いに応じで価格差別すべきだが、所得格差から生じる問題に対して、
いちいち所得や資産を調べたりして(僻地ならできるかもしれないが)、
政府が個々の財ごとに価格規制で対応するよりも、所得再分配という対処策が個別にちゃんとある。
まずは所得再分配政策をきっちりとやる方が望ましい。
こういう考え方を「政策割当」の問題と言い、
ティンバーゲンの定理=複数の独立した政策目標を達成するためには、同じ数の政策が必要。
マンデルの定理=政策の諸手段は、それぞれが最も効果を発揮する政策目標に対して割り当てられるべきである。
などが有名。
価格規制という政策ひとつで、不平等の是正も同時に目標とするのは間違っており、
所得分配の平等化には所得再分配という適切な政策がちゃんとあるということ。
映画館やレストランでの学割やレディースデーなどのように、価格差別のために客を識別するのが簡単で、
再販不可能な財で、企業が勝手に価格差別を行うことに関しては、もちろん自由。
そのような価格差別が次の第3種。
・ 第3種価格差別
消費者1人1人については留保価格が識別できなくても、グループ(市場別)でなら識別可能な場合、
それぞれの市場の価格弾力性の違いに応じて価格差別を行うのが第3種。
大人と子供とか、社会人と学生、男女など。
時間は無いけど金はある社会人は、需要の価格弾力性が低く、多少値段を上げても需要は減らない。
一方、価格に敏感な層は、需要の価格弾力性が高いので、値段を下げることでかえって企業の収入が増える。
「ヴァリアンの入ミク(9版)の26章4節、p422~p423」より、
価格弾力性が大きい方の市場1の逆需要関数:P1
価格弾力性が小さい方の市場2の逆需要関数:P2
それぞれの市場に、独占企業が供給するので、費用関数は、
C(Y1+Y2)
独占企業が直面する利潤最大化問題は、
P1・Y1+P2・Y2+C(Y1+Y2)
完全競争下での利潤最大化条件はP=MCだが、独占市場ではMR=MCなので、
MR1=MC(Y1+Y2)
MR2=MC(Y1+Y2)
限界費用は等しいので、限界収入も各市場で等しくなければならない。
限界収入MRは、総収入関数TR=P・Yを、需要量yで微分すると求まるので、積の微分を用いると、
∂TR dP Y
────=MR=P+P'Y=P(1+───・──) ・・・1
∂Y dY P
需要の価格弾力性をεとすると、
dy P dY P
ε=───・── → │ε│=-───・──
dP Y dP Y
従って1式は、
1
MR=P(1-───) ・・・2
│ε│
よって各市場の利潤最大化条件は、
1
P1(1-────)=MC(Y1+Y2)
│ε1│
1
P2(1-────)=MC(Y1+Y2)
│ε2│
市場1の方が価格弾力性が大きい場合、
1 1
1-────>1-──── → │ε1│>│ε2│
│ε1│ │ε2│
MC(Y1+Y2)は各市場で共通なので、
P1<P2
となる。すなわち、価格弾力性の大きい市場1では低価格、価格弾力性の小さい市場2では高価格となる。
・ ラーナーの独占度
2式と、独占市場での利潤最大化条件のMR=MCより、
1 1
MC=P(1-───) → P=MC・[────────] ・・・2F
│ε│ 1-(1/│ε│)
1
[────────]=マークアップ率(限界費用にどれくらい上乗せして価格を釣り上げているか)
1-(1/│ε│)
2F式を変形すると、
1 P-MC 1
MC=P(1-───) → P-MC=P/│ε│ → ─────=─── ・・・2G
│ε│ P │ε│
独占価格と限界費用との乖離率は、需要の価格弾力性の逆数に等しく、ラーナーの独占度という。
文献によっては、マークアップ率=ラーナーの独占度と表現しているものもある。
・ 固定費用と内部相互補助
第3種価格差別において、│ε1│>│ε2│だとすると、固定費用次第では、
価格弾力性が小さくて高価格を付けられる市場2だけに財が供給されて、
価格弾力性が大きくて低価格しかつけられない市場1には供給されない可能性もある。
しかし、ユニバーサルサービスの供給を義務付けた場合、さらに場合分けが考えられ、
ケースA:市場1への供給義務+価格差別はOK
ケースB: 〃 +価格差別も禁止
数値例次第では、ケースAは企業の参入が可能でも、ケースBは不可能な場合がある。
例えばケースAは、価格差別したところで、市場1では相変わらず利潤は負のままだが、
市場1+市場2=市場全体では、市場2だけ供給した場合よりは利潤は減るが、利潤は正となる可能性がある。
ところが、同じ需要条件(市場条件)と固定費用の下で、ケースBでは価格差別もできないので、
市場1+市場2=市場全体でも利潤が負となる可能性がある。
また、両方のケースで参入できたとしても、元々、固定費用のせいで、市場2では正の利潤、市場1では負の利潤
だったので、ユニバーサルサービスを義務付けている時点で、市場2の利潤によって、市場1の赤字を補っている
ことになり、内部相互補助という。
○ P203~P205、ティブーの足による投票モデルと地価。
1つ上の林公共の所で説明した、資本化仮説の話に該当。
アメリカのように地方交付金による地方間の所得移転が少ない国では、
地方公共財が良質で多量の地域の地方税は高くなり、その逆は低くなる。
従って、地方公共財が地価に与える影響は小さい。
P202にもあるように、地方公共財の理論(やティブーのモデル)は、
各地方自治体の人口が多く、かつ、地理的に遠く離れて、分散して点在していて、
相互依存関係の少ない(スピルオーバーの問題がない)、アメリカのような環境で生まれたことにも理由がある。
逆に日本のような地方交付金や補助金による所得移転が多い国では、
地域ごとの居住者に課せられる地方税そのものについては格差は小さい。
その分、地方公共財の影響は地価に反映される。
地主達の間では、良い公共財(公園など)は誘致合戦となり、悪い公共財(ゴミ処理場)などは敬遠される。
一方、借地・借家・借マンションなどの借り手は、公共財の影響は地価や賃貸料に反映されるので、
自分の選好に見合った地域に移動して、足による投票を行いやすい。
結局、地方交付金などによる所得格差の是正は、その名目とは裏腹に、
地価の上昇によって富裕層である地主達に吸収される。
○ P213~P216、クラブ財(地方公共財)の最適規模と不安定性
ティブーの足による投票仮説(地方公共財の市場均衡的解決)が成り立つためには、
各規模のクラブ財に対して、それぞれ需要する人数が十分大きくなければならない。
多種多様な規模のクラブ財が並存できることによって、競争が働き、市場均衡は達成される。
大都市のテニスクラブや劇場などがその例にあたる。
問題となるのは、
最適クラブ員数(N*)>総需要者数(N) ・・・1
その場合、平均費用逓減産業と同様になり、全員を同一のクラブに参加させるのが望ましい。
平均費用が逓減している区域では、限界費用はそれより小さいので収支が合わず、操業停止せざるを得ない。
強制的な費用徴収による非市場的な解決が必要となる。
もし1式とは逆に、N*<Nとなっていても、N*がNの1/2以上あるような場合、
この社会は2つのクラブを支えるには人口が少なすぎ、1つでは多すぎることになる。
N*がNの整数倍でないときは、クラブ財の自発的供給は不安定となる。

1人当たり費用(平均費用)が最小となる最適クラブ員数は、N*となる。
仮に、総需要者数N>N*だったとしよう。しかし、N/2<N*となっている。
もし2つのクラブを作って半数ずつに別れた場合、1人当たり費用=会費は、OBからOEへと下がる。
しかし、限界費用OFは、平均費用OEより小さい。
このとき、各クラブにとっては、1人追加することによる限界費用は平均費用より小さいので、
1人追加することでかえって1人当たり平均費用を減らすことができる。
引き抜かれた側にとっては、MC曲線はずっと右上がりなので、かえって限界費用が下がる。
そこで引き抜いた側が提示した条件より、さらに有利な条件で引き戻しを図るだろう。
全員が引き抜きの対象である以上、誰も「限界費用以上の会費」を支払わなくなるが、
それだと平均費用に満たないので収支は均衡せず、クラブ財の自発的供給は不可能となる。
大都市だと複数の球場が安定的に並存するのに対し、小都市では球場数が1つだと高利益なので、
2つ目を作ると両球場とも採算が取れなくなって、球場数が1になったり2になったりを繰り返すのに似ている。
数式、グラフ、数値例を用いた、もっと詳しい分析を学びたい場合は、本書を読もう。
最後に、P200~P203に戻ろう。ティブーの足による投票仮説が成立するための条件について。
1:所得獲得のための地域制約がない
2:地方自治体ごとに異なる地方公共財メニューについての完全情報
3:多種多様なメニュー(地方公共財のミックスパターン)があり、かつ、同質なメニューの供給も多数存在
4:1人当たり平均費用が最低となる最適人口規模の存在
5:便益がスピルイン・スピルアウトしない
6:地域間移動にコストが掛からない(法的・経済的)
7:地方公共財について同一の選好を持つ消費者も多数。
結局、完全競争市場的な条件が必要となる。
1についてティブー自身は、利子・配当所得、年金だけで生活する消費者を仮定。
3は種類(各財ごとの市場)そのものが多数で、1種類ごとの市場においても供給独占なし、
5は外部性(スピルオーバー)なし、6は取引費用なし、7は需要独占なし。
4については、最適サイズが無い場合、あるいは最適サイズが極端に大きい場合、
非競合財となって全員消費が望ましいことになる。
後者だと、平均費用逓減財を意味するので、地方公共財に規模の経済が働いていることを意味する。
前者だと、上記のクラブ財の最適規模で学んだように、地方公共団体間で居住者を奪い合ったり、
公共財供給が国になったり地方になったりと不安定になる。
○ 6章の所得分配
P231~P233の、現金給付vs現物給付。
西村の入ミク(黄緑色の第2版)では、4章4節、無差別曲線の応用、
岩菊と飯田のゼミナール経済政策入門の3部、P369~P372、のそれぞれに同じ内容の説明がある。
○ 7章の公共選択
複数の選択肢に対して、任意の2つを1つのペアとして多数決投票を行い、
勝者同士でまたペアを作り、同じ多数決で勝者を決めていくトーナメント方式の投票方法を、
単純多数決ルールといい、(コンドルセの)投票のパラドックスが起きる。
また、選択肢が奇数(A,B,C)で、まずAとBの多数決を行い、勝った方とCの多数決を行う場合、
後出しのCがかなり立場的に強くなる。
人々は自分の選好に従って純粋に投票しているつもりでも、提案順序を議会や官僚に操作されている可能性がある。
そもそも、上記のような投票方法は、序数的選好を示すだけで、基数的選好を示すことができない。
パラドックスが起きないような投票方法として、順位投票制、点数投票制(ボルダ投票)などがある。
前者は順位を付けた後、選択肢ごとに順位を合計する。後者は最初に同じ持ち点が各自に与えられて投票する。
ペアごとではないので、選好の強度を反映しやすく、最終的に集団全体の選好もかなり正確に表現する。
ただし、票の取引(ログローリング)という戦略的行動を防ぐことはできない。
P269の注釈より、ログローリングはアメリカの政治ジャーナリズムの用語で、
開拓時代に協力して木材を転がして運び出したことから来ているが、
文芸家達が作品の売り上げを伸ばすために、互いの作品を褒め合うことを指す場合もあるとのことw
一見、政策が違う政党同士が連立を組むのもそれが理由。
ブキャナンとタロックは、取引というのは資源配分上も、厚生配分上も望ましいので
ログローリングも望ましいと論じたが、常に社会厚生上望ましいとは限らない。
取引はその当事者双方に利益をもたらすことは間違いないが、
その決定自体は全ての人に影響を及ぼすので、取引に参加していない第三者にも外部効果を及ぼす。
その数値例がP270~P271の表7-D。
取引が無かった場合より、取引した場合の方が、社会全体で利益が減っている。
この数値例も見事なので、興味ある人は図書館とかで見つけて読んでみよう。
暗黙のログローリングというのもある。投票する人々はログローリングしていないつもりでも、
提案された選択肢が、複数の政策案の抱き合わせ(A,B,C)になっている場合、
BとCはそれほど好きじゃないが、Aを強く選好しているため、仕方なく一括案に投票するという話を、
現実でもよく耳にするだろう。大体において、人質に取られるAは、景気、雇用、所得である。
そして、どの政策案を一括にするのかも、議会や官僚が操作する権限を握っている。
7章4節、P274~P278、直接投票と間接投票についてのパラドックス、
7章5節、P285~P290、最小勝利提携、
について、ちょっと数値例の話が長いので、 雑記ノートで。
・ 「J.R.マークセン W.H.ケンプファー K.E.マスカス 国際貿易―理論と実証〈下〉 多賀出版 2000/09」
の19章、P389~P409、貿易政策の政治経済的分析。
柴田公共のP278~P281、有権者の行動(取引費用、合理的無知、囚人のジレンマ)と同内容で、
こちらのマークセン=ケンプファーの教科書で説明しよう。
19.2節、P391~。基本となる中位投票者モデル。
ストルパー=サミュエルソンの定理から、労働集約的な輸入財の国内価格を引き上げる関税は、
どのセクターに関係なく、労働の実質賃金を引き上げ、資本の実質レンタル価格を引き下げる。
人口全体を1として横軸に取り、縦軸に利益を取る。中位投票者は分布のちょうど0.5に位置する。
さて、この関税政策によって、60%の人が損失を被るとし、1人当たり損失をL、
利益を得られる残りの40%の、1人当たり利益をGとしよう。

GとLは、横軸を挟んで上下に対称とする。すなわち、G=Lとする。
原点から0.6の所までは損失グループを並べて、0.6の所から不連続となる。
0.5に位置する中位投票者は損失Lを被るのだから、関税法案は否決されるだろう。
19.3節、P393~。前節では、G=Lであった。そこで設定を変えてみよう。対象は貿易自由化政策とし、
G’>L’ かつ 0.4G’>0.6L’としてみる。

0.6×L’=長方形Aの面積で、グループL’の総損失。
0.4×G’=長方形Bの面積で、グループG’の総利益。
貿易自由化法案によって、社会全体が得られる純利益は正(A<B)である。
しかし、中位投票者の定理により、法案は否決されてしまうのである。
パレート効率性の基準で言えば、損失を受ける人がいる限り、そのような政策はパレート効率的ではない。
しかし、その基準だけだと採用できる政策が限定的になる。
そこでカルドアの仮説的補償原理によれば、利益を受けた人が損失を受けた人に補償して、
それでもなお利益が確保できる場合には、たとえその補償が実際には行われなかったとしても是認される。
このような補償は、票の買収に等しく、ログローリング(票の取引)に等しい。
しかし、すぐ上で述べたように、ログローリングが常に望ましいとは限らない。
アメリカで1930年に、スムート=ホーリー法(Smoot-Hawley)が、
ログローリングによる厚生低下の教科書的な事例としてかなり有名。
各産業の支援を受ける議員同士が、他のセクターの関税にも賛成し合った結果、
平均保護関税が輸入額の50%以上にまで上昇したという。
中位投票者定理が成り立つためには、自分の利得に関して完全に知っていること、
そして忠実に自分の選好に従って投票することを仮定する。
しかし利得を理解するためには、費用をかけて情報収集しなければならない。
さらに投票所に行って投票すること自体にも、時間や労力などの費用が掛かる。
これらの費用は、政治参加による利益と比較されなければならない。
自分の一票が選挙結果を左右する可能性はゼロに近い。
個人の投票という行動から得られる期待利得(確率を考慮した利得)はかなり小さく、
一方で投票にかかる費用を考えると、無知なまま棄権しておいた方が合理的かもしれない。
P398~。関税によって特定の産業を保護するケースで、今度は、利益を受けるグループはたったの5%、
損失を被るグループは大多数の95%としよう。
しかし、1人当たり利益のGは非常に大きく、一方で1人当たり損失のLは非常に小さいとしよう。
(コメの輸入規制で、米の値段が少々上がったところで、1人当たり損失は微々たるものだったり。)
G>>>>>L

それでも社会全体では、0.95L>0.05Gとする。ネットで社会厚生は低下(A>B)する。
このような場合、利益を受ける小グループは、組織的な投票行動(お互い監視し合ったり)の費用に比べて、
利益の方が大きいので、積極的に活動できる。さらに重要なのが、そういう活動にあたっての資金面である。
このような活動費は、投票後に得られる利益から提供される可能性すらある。
このような活動を、レントシーキングという。
レントとは超過利潤のことであり、大抵の場合、参入規制や保護政策によって作られる独占利潤である。
19章4節、P400~。不確実性のもとでの中位投票者モデル。
貿易自由化政策の話に戻ろう。60%の人が+Pの利得を得るグループB、
40%の人が-Pの利得(つまり損失)を得るグループAとしよう。
社会全体の純利益は、0.6P-0.4P=0.2Pなので、貿易自由化政策は実施されるべきである。
一方、輸出セクターで用いられている生産要素は40%とし(Bに属している)、
その40%の人達は貿易自由化後の厚生増加について正確な情報を持っているとする。
残りの60%のうち、1/3(20%)の人達も+P(Bに属している)、
2/3(40%)の人達が-P(Aに属している)となるのだが、
この残りの60%の人達は、厚生が高まるのか、それとも低下するのか不確実だとしよう。
すると、この残りの60%の人達の期待利得は、1/3P-2/3P=-1/3Pとなる。
つまり、自分がAなのか・Bなのか、利得を得るのか・損失を被るのか、情報を持っていないが故に、
確率的に期待利得はマイナスと考えてしまい、全員が反対票を投じることになる。
従って、中位投票者モデルの下で、貿易自由化法案は否決されてしまう。
例えば世界の生産能力が向上し、国内の農業の生産費用が相対的に高くなったとしよう。
関税や輸入数量割当などの政策が採られなければ、農業に従事する生産要素の所得を脅かすだろう。
このとき、貿易自由化政策は一国全体の厚生を高めるとしても、
直接に農業とは関わりのないセクターの生産要素であっても、その効果は不確実なのである。
自身が同じ立場に立たされた場合に保護を受けるための暗黙の保険として、
産業保護政策を支持することは十分にありえる。
「現状維持への偏り(status quo bias)」と呼ばれ、
このタイプの保護主義は、「保守主義的社会的厚生関数」と呼ばれるもので説明される。
つまり、とにかく現行のセクター別の所得分布を一定に維持するのが目的となる。
○ 次の板谷公共の15章4節、P373~P377、ニスカネンの(官僚の)予算最大化モデル。
柴田公共では、P281~P285で同内容。
板谷公共の記述の方を中心に書くが、同じ話題が続いた方がまとまるのでこちらに書く。
売上高最大化仮説の政府版モデルである。
そもそも公共財の供給は、政府による供給独占となっている(対民間に対して)。
また、立法や行政の実務を担当する行政府(各省庁の官僚)は、
公共財供給に関する生産関数や費用関数などの技術情報に関して、
立法府(政治家)よりも詳しいという意味で、情報の非対称性が存在している(対議会に対して)。
さらに、情報の非対称性だけではなく、官僚が作成した予算案を、承諾するか・しないかを迫るように、
議会に提出することが制度的に認められている。
これがまた結構重要で、情報を握っているだけではなく、議会に対してかなり強い交渉力を持つ。
(一般的にAさんとBさんで考えるとわかりやすいだろう。はいといいえしか選択肢の無いAさんはつらい。
細かいメニューを注文できないし、いいえと言っちゃうと、最大で利得は0なので、飲まざるを得ない。)
予算を含めた立法作業について、政治家と官僚の間には、プリンシパル-エージェント関係がある。
しかし、情報の非対称性があると、依頼者(プリンシパル)の利益よりも、
代理人(エージェント)自身の利益を追求するようになる。
これをエージェンシー問題といい、それによって発生するプリンシパルにとっての不利益や非効率、
あるいはモニタリングコストも含めたコストを、エージェンシーコストという。
官僚にとっての自己利益(効用関数)とは、金銭的収入や雇用の安定だけではなく、
名声・評判・名誉・地位、社会的貢献、忠誠心、プロ意識などの、非貨幣的所得も含まれる。
そして、これら多くの目的を達成する上で、何より必要となってくるのが、
自らが所属する組織の維持・拡大=予算の獲得である。
とにかく予算を獲得し、組織を拡大できれば、上記の目的から得られる効用は全て増加するからだ。
そこで、公共財から得られる便益の関数をB(G)としよう。
国民にとっての留保価格(支払意思額)なので、B(G)=予算と言える(便益分だけ税金を払ってくれる)。

限界便益は逓減(B'(G)>0だが、B''(G)<0)、
限界費用は逓増(C'(G)>0であり、C''(G)>0)。
公共財供給の効率的水準は、限界便益=限界費用(B'(G)=C'(G))となる、E点およびG*点である。
しかし、官僚にとっての効用最大化水準となる公共財供給量は、F点およびG+点となる。
官僚の効用最大化問題を解いてみよう。まず、官僚にとっての制約条件は、B(G)≧C(G)である。
情報の非対称性より、議会は費用関数C(G)の形状を知らないので、
費用C(G)が予算B(G)をオーバーしない限り、その予算案は通るからである。
一方、予算であるB(G)が、まさに官僚にとっての目的関数となる。ラグランジュ関数は、
L=B(G)+λ[B(G)-C(G)]
最適化の1階の条件は、∂L/∂G=0と、∂L/∂λ=0なので、
λ
B'(G)=────C'(G) および B(G)=C(G)
1+λ
B(G)=C(G)となる点は、原点とF点があるが、λ>0なので、B'(G)<C'(G)となる。
(制約条件のB(G)≧C(G)は、不等式制約なので、厳密にはクーン=タッカー条件となる。
相補性条件より、B(G)-C(G)=0ならば、λ>0である。)
従って、F点およびG+点が、効用最大化(予算最大化)の水準となる。
上記のラグランジュ関数を見てもわかると思うが、柴田公共のP284より、
官僚が一般人と異なる行動原理となるのは、官僚だけが特殊な効用関数をしているからではない。
官僚が一般人と比べて非倫理的なのではなく、一般家計とは異なる制約条件に直面しているからである。
一般人の誰しもが、同じ制約条件に直面すれば、同じ行動を取る。
効用関数に非貨幣的所得が含まれているかもしれないが、官僚だけではなく民間にもある。
従って、官僚の非効率を正すには、効用関数の方ではなく(心を入れ替えろと道徳心に問い掛けるのではなく)、
直面している制約条件、すなわちシステム(制度)そのものを変える必要がある。
上記のエージェンシー問題も、情報の非対称性の解消とインセンティブ設計が必要となる。
情報公開、モニタリングやチェック、責任と罰則。(エージェンシー問題の詳細は、組織の経済学を参照。)
● 「板谷淳一 佐野博之 コア・テキスト公共経済学 新世社 2013/01」
○ 9章、コモンズの悲劇(共有地の悲劇)。柴田公共のP87~P94も混ぜて一緒に説明する。
山・海・河川・大気などは再生可能資源(非枯渇性資源)と言われ、一定の浄化能力や再生産能力がある。
その一定の範囲内であれば、採取したり利用しても資源全体として減らないという意味で、
その共有地(の資源)はストックとして考えられる。
ところが、その一定の能力を超えるような汚染や乱獲があると、ストックそのものが減少する。
所有権が確定しておらず、共有地(コモンズ)となっている資源に対して、
オープン・アクセス(自由参入)になっていると、過剰利用や過剰採取が起きる。
自分がストックを維持しようとして今日の収穫を手控えても、明日は他の人に収穫されてしまう。
囚人のジレンマになってしまいそうなことが、この段階ですでにわかる。
自分の収穫や利用が、相手の収穫や利用を減らすという意味で外部性があり、混雑現象とも言える。
1:ストック(共有地)は大きいほど収穫・利用しやすい。Nを利用者数、Sをストックとすると、
Y=F(N,S) ∂F/∂N<0 ∂F/∂S>0
Yは1人当たり収穫量を表し、右辺のFは収穫関数という。
ストックが小さくなるほど同じ収穫量にかかる費用は大きくなるので、∂F/∂S>0となる。
混雑費用(∂F/∂N<0の影響)も、収穫関数の方で表す。
Nの効果やSの効果とは別に、1人当たりの生産活動にかかる費用をwとする。
生産物の価格をPとすると、本来ならP=MCが利潤最大化条件なのだが、上記の設定の下での最適化問題は、
利潤関数:NPF(N,S)-wN=[PF(N,S)-w]N
をNで微分して0と置かなければならない。
∂F(N,S)
PF(N,S)+NP──────=w ・・・9.1
∂N
ちゃんと収穫関数の中のNまで考慮して、最適な利用者数Nを求めているということは、
利用者全員で1つの会社を作って、利用者数を制限(コントロール)しながら共同利潤を考えているに等しい。
∂F/∂N<0より、9.1式の左辺の2項目は負となり、
Nが大きくなることによる収益の低下をちゃんと反映している。
一方、共同利潤を考えずに、オープンアクセスによって個人個人が自分だけの利益を考えて生産すると、
PF(N,S)-w>0である限り参入してしまう。仮定により、∂F/∂N<0なので、最終的に均衡では
PF(N,S)=w
となるまで参入が続くだろう。この条件は利潤関数をNで割っただけであり、
平均生産物価値=平均費用
9.1式の利潤最大化条件を考えると、2項目が無視されており、過剰収穫になっていることは明らかである。
この1の説明は、共有地の利用者数が多いケースで、少ないケース(例えば2人)だと
囚人のジレンマのように非協力ゲームで説明されることが多い。相手の戦略を与件として、自分の最適戦略を求める。
市場需要全体に対して、相手の生産量を所与として、自分の利潤を最大化するような最適反応戦略と来れば、
クールノーモデルであり、実は共有地の悲劇と数式的には同じ構造となる。
板谷公共の9章の3節にその説明があり、他の教科書だと
「中山幹夫 はじめてのゲーム理論 有斐閣 1997/09」の3章3節にもある。 ゲーム理論ノートにも引用した。
ただし、板谷公共のP218によると、数値例次第では囚人のジレンマにならず、
パレート効率的な利得が実現する場合もあるとのこと(P219の表9.2)。
オープンアクセスで参入が容易だからこそ悲劇が起きるのだから、
上記の記号で言えばwが大きくてそもそも参入できず、結果的にパレート効率的な収穫量と同じになる可能性もある。
2:ストック外部性。柴田公共のP87~P94。
1の収穫関数から求まる収穫量が、今期のSに対応したストックの成長量以下なら、Sは減らない。
1の定式化で、NとSはそれぞれ独立のように見えるが、実はNが増加すれば来期のSは小さくなる。
このような外部不経済を、ストック外部性という。
逆に言えば、1の問題はNで偏微分して最適人数を考察しているが、そのNの変動にあわせてSは変化しない。
考慮されているのは、9.1式の2項目の「混雑費用によるフローの減少」だけである。
より詳しく見ていこう。再生可能資源は、生産能力のある資本ストックのように、
資源そのものを自ら新たに生産し(フロー)、そのフローが新たに追加されることで、ストックそのものも増やす。
資源(ストック)の成長率が10%ならば、そのフロー部分を消費しても、ストック全体は減らない。
同じ量のストックを毎年残せるので、永久にその10%分のフローを消費し続けることができる。
もし、10%以上に乱獲して、過剰利用・過剰採取してしまうと、ストックそのものを減らしてしまう。
ただし、フロー部分を消費しなければ、無限に成長し続けるかというと、そうでもない。
フローの量は、ストックの量に依存し、魚で言えば、生息数が多くなるにつれて、
ストックの成長率も大きくなっていく(ストックの絶対値だけが大きくなるのではなく、その成長率も大きくなる)。
ところが、生息数が多くなり過ぎると、エサ不足(混雑減少)となって成長率は下がり始め、
いつか成長率は0となってストップする。
一方、生息数が少なくなると、子孫を残すためのパートナーを探すのが難しくなり、
出生率が下がり、たとえストックが増加したとしても、成長率は低くなる。
(ストックの絶対値が小さくなるだけではなく、その成長率も小さくなる。)
最悪の場合、ストックが小さくなりすぎて、自然回復(自然再生)できなくなり、
成長率がマイナスとなって、絶滅の道を回避できなくなる可能性もある。

横軸=ストック量(St)
縦軸=ストックが生み出す増加量(フロー量)=⊿St=St+1-St
フロー=St+1-Stというのは、どういう意味なのかというと、
例えばC点では、今期のフローがプラスなので、今期のストックに追加されて、来期のストックそのものが増える。
すなわち、t+1期には、ストックはC点より右側に来ている(例えばD点)。
ストックがある値に決まったら、それ以後ずっとその値を取り続けるわけではなく、
成長曲線で決まるフロー量に従って、横軸上の点は動き続けるのである。
そういう意味で、図2-10の成長曲線は、動学方程式ともいう。
さてC点を越えると、横軸のストックが増加するにつれて、混雑減少(エサ不足)によって、
縦軸のフローは(プラスではあるが)減少していく。B点になると、飽和状態でそれ以上増えない。
横軸=縦軸の値が0の線 → ⊿St(フロー)=0
成長曲線と、横軸との交点では、もはやストックは不変となる。
そのような状態を定常状態と呼び、交点を定常均衡点(単に均衡点)という。
定常均衡点は2つある(複数均衡)。A点とB点だが、まずはB点から見てみよう。
B点より左側では、成長曲線は縦軸の値(フロー)がプラスなので、右に動く力が働く。
一方、B点より右側では、マイナスなので左に動く力が働く。
B点から出発して、少し左右に動いてしまっても、またB点へと戻る力が働くので、B点は安定的な均衡点という。
A点は定常均衡点ではあるが、少しでもA点より左右に動いてしまうと、もはやA点には戻らない。
A点は不安定な均衡点という。たまたま最初にA点出発じゃない限り、A点には到達しないし、
不安定なので、少しでも動くと戻らない。
A点より右側にいればとりあえずストックは増えていくので心配ないが、
人為的な乱獲や環境汚染、自然環境の変化や災害によって、外生的な変化や圧力が大きく加わることで
A点より左側に行ってしまうと、絶滅への道を辿ることになる。
A点は、種が絶滅するかどうかの臨界点(分水嶺)とも言える。

図2-11は、図2-10の成長曲線を、別表現したものであり、動学方程式と呼ぶことにする。
例えば、⊿St=aSt+b → St+1-St=aSt+b → St+1=(1+a)St+bとすることで、
縦軸を⊿StからSt+1に変更しているだけで、両者は同質の方程式である。
またこのような方程式は、t期の値が決まれば、それ以降順次St+1、St+2、・・・の値が決まっていく。
ストック量Stが時間を通じてどのように動いていくのか、その動き方を記述した方程式なので、動学方程式という。
ちなみに、離散時間だと差分方程式、連続時間だと微分方程式になる。
原点を通る45度線:St+1=St(x-y平面で言えば、y=xなので傾きは1であり、その角度は45度。)
図2-10の成長曲線と、横軸との間の垂直距離(=フロー=St+1-St)が、
図2-11の動学方程式と、45度線との間の垂直距離になっている。
例えば、図2-10のCC’の距離=図2-11のCC’の距離。
今期のストック(St)が、C点だったとしよう。
動学方程式に従って、t+1期のストック量(St+1)が、縦軸上で決まる。
しかし、話はそれで終わらない。縦軸上で決まったSt+1から、右に進んで45度線とぶつかった所が(D点)、
次の期に横軸で取るSt+1の値となる。
横軸上で決まったSt+1から、さらに動学方程式に従って、St+2の値が縦軸上で決まる。
以降、期が進むごとに、動学方程式と45度線の間を、右上にジグザグに進み、最終的にB点で均衡する。
図2-10に戻ろう。上記はフロー部分を消費しない話だった。
フロー部分をまるまる消費すれば、均衡点(AやB)以外でも、ストック量は不変となる。
例えば、E点とF点を例に取ろう。両点は同じフロー量だから、どちらも是認されるかというと、そうでもない。
F点の方がストックが大きいので、同じフロー量を捕獲・採取するなら、F点の方が費用が少ない。
そういう意味で、フロー量が同じというだけでは無差別とは言えず、E点は低位均衡、F点は高位均衡という。
そこで、ストック外部性も含めた共有地の悲劇の解決策として、
1:個人や1つの会社、1国が所有する。あるいは共同管理。
共有地の悲劇と来れば、オープンアクセスを防ぐための所有権の確定や、
あるいは組合による共同管理で生産や収穫をコントロールという話がセットになることが多い。
所有権の設定のケースは、小規模な共有地で、山林などではよくある話。
逆に海などは規模が大きすぎて費用が掛かりすぎるので、共同管理となることが多い。
2:ピグー税
9.1式で言えば、オープンアクセスによって無視されていた2項目を、ピグー税として課せば、
外部性は内部化されてパレート効率的になる。
しかし、共有地が多国間にまたがる場合は、統一政府が無いと難しい。
小規模で、混雑してきた時のピークロードプライシングなどは有効。
3:数量規制や禁猟(禁漁)期間の設定
柴田公共によると、禁止期間設定の場合は、解禁期間で相変わらず乱獲が起き、
短期的に大量収穫・生産するための大規模投資した設備が、禁止期間では遊休しているとのこと。
4:利用権(許可証)の売買市場
ピグー税は、限界外部費用曲線、市場供給曲線(産業全体の私的限界費用曲線)と市場需要曲線、
の3つの情報を政府が知っておかなければならない。限界外部費用+私的限界費用=社会的限界費用。
数量規制になると、個別企業の私的限界費用曲線の情報まで知っておかなければならない。
個別企業同士の限界利潤が等しくなるまで数量割当を行わなければならないからだ。
CO2排出権取引市場などは、排出権を与えれば(すなわち所有権を確定して内部化すれば)、
後は民間同士で勝手に取引が行われてパレート効率的になる。
その市場で決まる価格は、あたかもピグー税と同じ働きをする。
こっそり生産したり排出したりする監視費用については、ピグー税などと同じなので、その点で差異はない。
問題は、最初に排出権をどのように与えるかという配分問題。
均等配分すれば、元々排出の少ない企業が一方的に得をするし、
過去の排出実績に比例させるのも、それはそれで不公平となる。
ただし、配分が国別の場合、均等分配なら、それまで排出の少なかった発展途上国から、
排出の多い先進国が排出権を買うという形で、所得の再分配が起きるとも言える。
板谷公共ではアンチコモンズの悲劇も説明される。
発明品や医薬品の開発において、他の特許をたくさん使用しなければならない場合、
逆に所有権が細分化され過ぎて取引費用が大きくなり、開発を断念するケースも生まれる。
有用な資源の過少利用という意味で、逆の悲劇が生まれる。知的財産権の保護の問題は難しい。
○ 6章5節、P161~P162、マクガイアー・モデル
林公共のP210~P212にも同じ説明がある。
ティブー仮説はティブー自身は数式によるモデル化を行っておらず、マクガイアー(M.McGuire 1974)が、
クラブ財の最適供給モデルを若干修正することで説明。
地方公共財は1種類で、住民の選考は同一(異なる場合へ拡張すると、移動しあって最終的には同一同士となる)、
利用回数も固定(メンバー数をn、利用回数vとして、vを可変に拡張すると、
最適となるn×vを一定に保った状態で、vを増やせば、その分最適メンバー数nが減るだけ。)。
効用関数:U(x,G) ・・・1
予算制約:x+C(G,n)/n=I ・・・2
C(・)は費用関数。ちなみに同書の6.1節では、クラブ財の最適化条件を求めているが、
そことの定式化の違いは、混雑現象を表すnが、1式の効用関数に変数として入っている代わりに、
2式の中の費用関数にはnが入っていない。
混雑を効用の減少として表すか、混雑費用の増加として捉えるかの違い。
林公共の方では、消費者(住民)の予算制約:y=x+p(yは板谷で言えば2式のI、pはクラブ財の会費)。
クラブ財の収支均衡条件は、pn=C(G,n)。
さて、2式を1式に代入して、最適化する(微分してゼロと置く)。
U(x,G)=U(I-C(G,n)/n,G)
まずGについて微分してゼロと置くと、
∂U ∂C(G,n)/n ∂U ∂U/∂G ∂C
───[-────────]+───=0 → n──────=─── ・・・6.7
∂x ∂G ∂G ∂U/∂x ∂G
次にnについて微分してゼロと置くと、
∂U (∂C/∂n)n-C ∂C C
───[-─────────]=0 → ───=── ・・・6.8
∂x n^2 ∂n n
6.7式はサミュエルソン条件。限界代替率をn倍にしてるということは、
限界代替率を住民数(クラブ会員数)で合計しているに等しい。右辺は地方公共財(クラブ財)の限界費用。
一方、pn=C(G,n)をnで微分すると、p=∂C/∂n。
費用関数Cの中のnは、混雑費用を表わすのだから、クラブ会費pは、限界的な混雑費用と等しければ最適。
6.8式は最適人口規模を表す。限界費用曲線は平均費用曲線の最低点を下から上へと突き抜けるので、
限界費用=平均費用となるのは、平均費用が最小となる点である。
柴田公共の5章のP207~P212では、6.8式を図解だけで導出し、
(∂C/C)/(∂n/n)=1(弾力性が1)と表現している。
林公共(P212)によると、平成の市町村合併も同理論から説明でき、
人口規模を確保して平均費用を最小化することで、住民の効用を最大化。
この理論をベースに、公共財供給の費用関数を推定して最適人口規模を求めると、
平均費用を最小にする地域人口は20万~40万とする研究が多いそうだ。
ただし、麻生良文先生のサイトによると、http://fs1.law.keio.ac.jp/~aso/guide.html
「最近では,市町村合併に関して誤った議論が横行しています。
よくある議論は,市町村の最適人口規模を実際のデータによって求めると
人口規模が15万とか20万くらいのところで住民一人あたりの歳出規模が最低になる。
だから,行政事務の効率化のために,市町村合併を推進すべきだという議論です。
ちょっと考えてみればわかりますが,最適な規模は,地方政府の供給するサービスの便益が
どの地理的範囲まで及ぶのかに大きく依存します。
人口密度の高い地域と低い地域がありますから,それらを一緒にして議論することはナンセンスです。
また,現行の制度のもとで費用が最小になるような人口や面積の規模があったとしても,
それは現在の中央と地方政府の役割分担や,政府がどの程度私的財を供給するのかに依存します。」
地方交付税に関する説明も大事。
「地方交付税や補助金についても,あまり理論的な議論が行なわれていません(専門家の間でも)。
地方財政のほとんどの本では,「財政力の格差」を是正するために
地方政府間の財政調整制度が必要だと書いてあります。
ある地域に高所得者が多いために,税収格差が発生している場合,地域間の再分配ではなく,
個人を対象にした再分配を行うべきです。
(すなわち、所得再分配は地方ではなく国の役割。地方が担うべきなのは準公共財である地方公共財。)
地域を対象として再分配を行うと,豊かな地域の低所得者から
貧しい地域の高所得者に再分配が行われるかもしれません。」
○ 10章、租税競争(水平的財政外部性と垂直的財政外部性)。
・ 10章3節、P236~P239、まずは水平的財政外部性について。
租税競争の参加者が少数(例えばプレイヤー数2で、地域1と地域2)の場合、
相手の税率を与件として、こちらの税率を決めるという意味で、非協力ゲーム的な構造となる。
資本は移動できるが、労働者は移動できないと仮定。
人口規模が同じで、L1=L2=1と基準化(後でこの設定を変更してみる)。
各地域に企業は1つだけとし、地域1と2の企業の生産関数は1次同次で、同一とする。
Y1=F(K1,1) Y2=F(K2,1)
このように設定するのは、地方間の税率の違いによる資本移動の効果だけを分析したいためで、
その他の条件を一定としたり、簡略化したり、等しくしている。
さて、一般的な分析では、利潤最大化条件から資本の最適量を決める(資本需要関数を求める)。
機会費用としての利子率と、資本の限界生産力が等しくなるように、裁定条件が成り立つ(どちらで運用しても一緒)。
しかしここでも、資本移動の効果だけを分析したいので、資本の総供給量は固定とする。
_ _
資本市場の需給均衡条件式:K1+K2=K (教科書では、K=2と基準化)
需給量は変化しないが、じゃあ何の価格差に応じて、どんな裁定行動を取るのかというと、
地方政府間の税率の違いに応じて、資本の移動によって裁定取引を行う。
∂F(K1,1) ∂F(K2,1)
裁定条件式:───────-t1=──────-t2
∂K1 ∂K2
(∂Fi/∂Ki)-ti=税引き後の(限界)資本収益率 i=1、2
地域1の企業(以下、企業1)の資本需要関数を求めると、
裁定条件式は、本来なら右辺は市場利子率rになるが、上記のような設定となる。
_
そして、資本の需給均衡条件式から、K2=K-K1を代入することで、
K2の部分を消して、K1だけの式にして、K1=右辺(t1とt2のみの関数)となる。
(なぜなら、労働量は1で基準化してるので、生産関数の変数はKのみだから。)
基本的には、K1はt1の減少関数で、t2の増加関数となる。
- +
企業1の資本需要関数:K1=t1とt2のみの関数=K1(t1,t2)
_
企業2の資本需要関数を求める時は、裁定条件式に、K1=K-K2を代入して、K1を消せばいい。
すると、生産関数が同一であることから、
+ -
企業2の資本需要関数:K2=K2(t1,t2)
また、資本需要関数とは言っているが、資本の総供給量は固定されいているので、
結局は資本を移動させる行動原理(インセンティブ)を意味する。
さて次に、地方政府はどのように税率を決めているのか(どんなインセンティブがあるのか)、
家計の効用最大化、企業の利潤最大化のように、地方政府はどんな最適化行動を行っているのか。
まずt1やt2は資本に対する税率なので、その税収を移動しない労働者に移転所得として再分配を行うとする。
そして地域住民である労働者の所得を最大化するように税率を決める。
しかしここでトレードオフというかジレンマが生じる。税率を上げすぎると企業(資本)に出ていかれてしまう。
予算や費用関数などの制約条件の下で、最適化を行わなければいけないように、無限に税率を上げることはできない。
このような労働者の所得最大化問題を解くために、まずは目的関数である労働者の所得は、
∂F(Ki,1)
Ii=F(Ki,1)-───────・Ki+tiKi ・・・10.3
∂Ki
1次同次の生産関数とオイラーの定理(完全分配定理)より、収入(売上げ)は生産要素に分配され尽くす。
経済数学ノートの 「21:オイラーの定理」を参照。
労働所得Iiは、10.3式の1項目の生産量から、2項目の資本の所有者に支払われる資本所得を引いて、
資本への課税から得られた租税収入は、そのまま労働者への移転所得とする。
資本所得が(∂F/∂K)・Kとなっている理由は、実質資本コストをrとすると、資本所得はrKであり、
利潤最大化の下では、資本の限界生産力=実質資本コスト(∂F/∂K=r)だから。
10.3式のKiの部分に、企業iの資本需要関数を代入して、Kiを消せば、
(資本需要関数と連立している時点で、資本に移動されちゃうことを制約条件として考慮してることを意味する。
効用最大化問題を解くときに、効用関数の中に予算制約式を代入して微分して0と置くのと一緒。)
今度は労働所得Iiが、t1とt2のみの関数となる。
そしてKiを消したI1とI2も、生産関数が同一であることから、t1とt2を入れ替えただけの同じ式となる。
最終的に地域iは、t1とt2のみの関数となった10.3式を最大化したいのだから、
地方政府にとっての操作変数であるtiで偏微分して0と置く。
偏微分するということは、例えば地方政府1は、t2をいったん所与(定数)として、
t1で偏微分することを意味する。
∂Ii/∂ti=0と置くので、すでに消したKだけではなくIも消せて、
最後に残る関数は、t1とt2の方程式となる(所与とした方は変数に戻る)。
それがまさに、両地域の最適反応関数であり、地域1と2ともに、t1とt2の方程式となるので、
t1-t2平面に両方程式を描いて、交点を求めたものがナッシュ均衡となる。
最適反応関数も、生産関数の同一性から、t1とt2を入れ替えただけの同じ式となる。
y=ax+bだったなら、x=ay+bとなるような感じで、横軸をy、縦軸をxにすれば同じグラフとなる。
従って、両方程式の交点は、原点を通る45度線上に存在することになるので、
ナッシュ均衡:t1=t2=t#
ナッシュ均衡となるt#は、パレート効率的な水準と比べて過少になる(引き下げ競争)。
もし協力して同じ税率を課せば、税率をもっと上げることができ、住民の厚生(労働者の総所得)を高められる。
その上手い説明がP238にあり、同一の生産関数で、同一の税率なので、資本需要関数より、
_
K1=K2 → K1=K2=K/2 (資本市場の需給均衡条件式より)
他方で、同じ税率を課せば資本移動の心配が無いので、t1=t2を同時に上げて行けば、
各地域の税収tiKiを増やせて、両地域の住民(労働者)の厚生を高めることができる(パレート改善)。
水平的財政「外部性」と言われる所以で、もし地域1が資本税率を上げると、資本が地域2へと移動してしまい、
地域2からすると、何もしていないのに、税収が増えて、地域2の住民の厚生が高まる。
地域1が地域2に対して、正の外部効果を与えていると言っていい。
逆に地域1が資本税率を下げると、地域2から資本が移動して来るので、
地域2は何もしていないのに、地域1のせいで勝手に税収が減って、厚生が低くなる。
地域1が地域2に対して、負の外部効果を与えていると言っていい。
協調して(協力して)一緒に税率を上げれば、両地域とも厚生が高まるのに、
租税競争によって税率をパレート効率的な水準よりも下げしまう(過当競争)。
租税競争のナッシュ均衡は、まさに非協力ゲームにおける非協力解(ジレンマ)である。
・ 10章4節、P240~P242、人口規模が異なる地方政府間の租税競争。
4節では、L1=1、L2=2とする。それ以外の設定は、すべて3節と同じである。
結論だけを述べると、まず資本需要関数が異なってくる。t1=t2だった場合、K1<K2となる。
なぜなら、裁定条件を満たすためには、t1=t2である以上、資本の限界生産力が等しくならなければならない。
地域2の方が労働量が多いので、資本の限界生産力が地域1と等しくなるまで、
地域1から地域2に向かって資本が移動し続けることになる。
P242では資本需要の税弾力性(∂Ki/∂ti)・(ti/Ki)を導出しており、t1=t2だった場合、
地域1の資本需要の税弾力性>地域2の資本需要の税弾力性
となるので、人口の少ない地域1は、人口の多い地域2よりも、税率を引き下げるインセンティブを持つ。
逆に人口の多い地域2では、多少税率を上げても、地域1の方に資本が移動してくれないおかげで、
税率を高くするインセンティブがある。労働量が多いため、それでも資本が来てくれると思っているのだろう。
ヘクシャー=オリーンモデルで言えば、相対的に労働量の多い国は実質賃金が低く、資本収益率は高いからだ。
後は3節の手順と一緒で、I1とI2のそれぞれに、K1とK2の資本需要関数を代入して、K1とK2を消し、
∂Ii/∂ti=0を求めてIiも消すと、t1とt2の方程式(地域1と2の最適反応関数)が求まる。
最適反応関数同士の交点であるナッシュ均衡では、t1<t2となる。
・ 10章5節、P243~P246より、垂直的財政外部性について。
水平的財政外部性のときとは違って、地方政府と中央政府は同じ課税ベースに対して参入するので、
共有地の悲劇(つまりクールノーモデル)と同じ構造となる。
資本の記号はKだけ。人口は1に基準化、国税をtC、地方税をtLとすると、同じKに両方が資本税として課される。
資本移動の問題は関係なくなるので、本来の利潤最大化条件式より(資本の総供給量も別に一定ではない)、
∂F(K,1)
企業の資本需要関数:──────-tC-tL=r ・・・10-5-1
∂K
労働量は1で基準化してるため、生産関数の変数はKのみなので、1式は、K=tCとtLのみの関数となる。
rは、企業にとって所与となるので、企業が操作できる変数ではない。
そして、K1とK2の区別も別にないので、資本需要関数は1式の一本だけである。
地方政府と中央政府の最適化問題は、住民の所得最大化だと同じ目的関数になっちゃうので、税収最大化とする。
税収を上げると、資本需要関数より、資本が減っちゃうというジレンマとなる。
しかも、例えば地方税率が上がれば、国は何もしていないのに国税収入が減ってしまうという意味で、
負の外部効果が働く。
中央政府の目的関数:税収=tC・K
地方政府の目的関数:税収=tL・K
操作変数はそれぞれの税率なので、資本需要関数を制約条件として目的関数に代入してから、
∂tC・K ∂tL・K
─────=0 ─────=0 ・・・10-5-2
∂tC ∂tL
どちらも、tCとtLの方程式(最適反応関数)となる。tC-tL平面に両方程式を描いて、交点を求めたものが
ナッシュ均衡となるのだが、1式と2式の構造を見れば分かるように、操作変数が違うだけで、後は同一である。
従って、最適反応関数は、tCとtLが入れ替わったような式となる。その交点であるナッシュ均衡は、
tC=tL=t# ・・・10-5-3
次に、そのナッシュ均衡がパレート効率的かどうかを調べるために、
国と地方が共同で(協力して)税収の「合計」を最大化してみよう。目的関数は、
(tC+tL)K=tC・K+tL・K ・・・10-5-4
となる。4式をtCで偏微分して0と置いたものと、4式をtLで偏微分して0と置いたものは、
式の構造を見れば分かるように、どちらも同一のKとなり、
K=0
最適反応関数はまったく同じで、一本しか導出できない。
元々、一本しかない資本需要関数の右辺は、tCとtLのみの関数なので、
K=0と置くと、tC-tL平面に一本のグラフ(tCとtLの方程式)が描かれるだけとなる。
そのグラフ上では、税収の合計を最大にするtCとtLの組み合わせが、無限にある。
そこで両政府が話し合って、試しに
tC=tL=t*
と、設定してみると(一本の最適反応関数のグラフと、tC=tLという原点を通る45度線との交点)、
ナッシュ均衡の税率よりも低くなる(具体的な数値例とグラフは教科書を参照)。
3式のt#を資本需要関数に代入し、求まったKと共に税収の合計を計算してみると、
tC・K=tL・K=t#K ナッシュ均衡の税収の合計=2t#K ・・・10-5-5
一方、t*を資本需要関数に代入し、求まったKと共に4式に代入してみると、
協力した時の税収の合計=2t*K ・・・10-5-6
となり、2t*K>2t#Kが示される(具体的な数値例とグラフは教科書を参照)。
すなわち、ナッシュ均衡の税率は過大に設定されやすい。
これは各政府が競争的に自分の税率を決めるとき、負の外部性を考慮せずに決めるためで、
必ずパレート効率的水準より税率は高く、税収は低くなる。
同じ課税ベースという共有資源を奪い合う、共有地の悲劇と同じ構造である。
・ 10章6節、P246~P249、公共支出外部性(公共支出競争)。
企業誘致のための公共支出競争や補助金競争も過剰になる。
水平的財政外部性とほとんど同じ構造で、L1=L2=1に基準化。
資本市場の需給均衡条件式:K1+K2=Kバー(教科書では、Kバー=2と基準化)。
公共支出競争なので、地方政府が操作するのはG1とG2になる。
税金は住民の方に課され(水平的財政外部性のときは資本に課税)、一括税Tiとする。
地方政府の予算制約式は、Ti=Gi。
生産関数F(Ki,1,Gi)の中には、最初からGiが入っている。
裁定条件式は、企業1と2の資本の限界生産力が等しくなるまで、資本が地域間を移動し続ける。
裁定条件式と資本市場の需給均衡条件式から資本需要関数を求めると、G1とG2のみの関数となり、
K1はG1について増加関数で、G2について減少関数(資本が地域2の方に移動しちゃうから)。
そして生産関数が同一なので、企業2の資本需要関数は、
企業1の資本需要関数の、G1とG2を入れ替えただけの式となる。
注意なのが、地方政府は住民である労働者の所得を最大化するのが目的となるが、
資本税は課されない一方、労働者には一括税が課され、移転所得も無いので、Ti=Giより、
∂F(Ki,1,Gi)
Ii=F(Ki,1,Gi)-────────・Ki-Gi i=1、2
∂Ki
資本需要関数(G1とG2のみの関数)を代入してKiを消し、操作変数はGiなので、∂Ii/∂Gi=0と置く。
例えばI1をG1で偏微分するときは、G2はいったん所与(定数)とする。
Iiも消せて、G1とG2の方程式(最適反応関数)となる(所与とした方は変数に戻る)。
地域1と2の最適反応関数も、G1とG2を入れ替えただけの式となる。
後は最適反応関数同士を連立させて、ナッシュ均衡(交点)を求めると、
G1=G2=G#
求まったナッシュ均衡であるG#を用いて、資本需要関数からK1とK2を求め、
最終的に求まったI1とI2の合計を、
I1+I2=I#
とする。ナッシュ均衡がパレート効率的かどうかを調べるために、
2つの地域が競争せずに協力して、住民(労働者)の所得の合計を最大化してみよう。目的関数は、
I1+I2=I*
I*をG1で微分して0と置いたものと、I*をG2で微分して0と置いたものは、まったく同じになるので、
最適反応関数が1本になる。無限の組み合わせの中から、仮にG1=G2=G*を選ぶと、
G*<G#
I*>I#
となることが示される(具体的な数値例とグラフは教科書を参照)。
企業を誘致するための補助金競争も過大均衡となる。一方、住民(労働者)も移動可能として、
住民向けの公共支出(教育や医療・福祉など)は、正反対の結果となる。
公共支出を賄うための租税負担が高くなってしまう高所得者(優秀な労働者や企業)が移動してしまうので、
福祉支出の切り下げ競争になるとのこと(もちろんこれまでと同様にパレート非効率的な過少均衡となる)。
結局、生産要素(労働や資本)の移動性を考慮すると、上記のように外部性(市場の失敗)が必ず発生する。
外部性と来れば内部化で、合併して共同で課税や公共支出を行うことだが、
そうなると究極的には中央政府による集権制になってしまう。地方分権性もメリットがあるので難しい問題となる。
EUでは租税協調という一種のカルテルを形成しようとしているが、なかなか難しいらしい。
理由は、各国家間の規模の違いで、規模の大きなドイツやフランスは便益を享受、
規模の小さい新加盟国などは損失を被るとのこと。
・ 10章の最後、P250~P251、水平的外部性を内部化するための定率補助金政策。
すべてを中央集権制にしてしまうのも無理があるので、地方分権性を維持しつつ、
財政的外部性を内部化する方法として、中央政府からの定率補助金政策を、
10章3節の水平的財政外部性のモデルで分析してみよう。
中央政府は、地方政府の公共支出Giに対して、s×100%の補助金を出すとする。
地方政府の予算制約式:(1-s)Gi=tiKi
10章3節のモデルでは、Gi=移転所得なので、
∂F(Ki,1) ti
Ii=F(Ki,1)-───────・Ki+────Ki ・・・10.10
∂Ki 1-s
後は同じ手順。資本需要関数を代入してKiを消し、操作変数であるtiで偏微分して0と置くと、
最適反応関数が求まるので交点を求めると、
tC=tL=sの関数
地方政府同士が協力して一緒に税率を上げなくても、競争状態のナッシュ均衡の税率に定率補助金を出すことで、
税率を同時に上げてやる効果が生まれる。結果、住民の所得(厚生)も増加し、パレート改善できることが示される。
○ 11章、ネットワーク外部性
FAXの例が有名で、利用者数が増えれば増えるほど、便益が高まる財。需要側の規模の経済とも言える。
個人の効用が、同じ財を消費する他人の人数に影響を受けるという意味で、外部性がある。
他の例として、同じワープロソフトを使う人が増えると、文書ファイルの互換性の心配が無く、
入門書の発行が多くなったり、困ったときに周りで助けてくれる人が増えたり。
本書ではスマホを例に採り、アイフォンとアンドロイドの話で説明している。
・潜在消費者=1000人
・留保効用(留保価格=限界支払意思額)Vは、見事なまでに全員異なり、100円刻みで、
10万円>9万9千900円>9万9千800円>・・・>千円となっているとする。
縦軸にV、横軸に人数、左から留保効用の高い順に並べると、
i番目の人の留保効用Vi=10万-100(i-1)=100100-100i ・・・11.1
価格をPとすると、Vi≧Pの人達は購入する(等しい場合は購入する・しないは無差別だが、購入すると仮定)。
i番目の人まで購入するということは、i=701ならば、需要量もそのまま701となる。
Vi=P → 10万100-100i=P → i=1001-(P/100) ・・・11.A
価格を3万円とすると、i=701となる。すなわち、11.A式はそのまま需要関数となる。
ただし、上記の話ではまだネットワーク外部性を考慮していない。
N=すでにアイフォンを購入している人の数
ネットワーク外部性とは、消費者数が増えれば増えるほど、その財を消費している人の効用が高まる。
逆に消費者数が少ない内は、ネットワーク外部性が無い財と比べて、かえって効用は低くなる。
その境界を100人とし、ネットワーク外部性による効用の増加を単純にN倍とすると、
ネットワーク外部性を考慮した限界便益=(N/100)Vi
Vi≧Pという基準は次のように変わる。
(N/100)Vi≧P ・・・11.B
新基準11.B式の下では、購入者数が100人未満のときには、他社の携帯電話との接続が多くなり、
通話料金の割引を受けられなかったり、アプリが少なくて、Viより小さくなる。
逆に100人以上に購入者が増えれば、元のViより大きくなる。
元々、留保効用は11.1式なので、ネットワーク外部性を考慮した上で、
改めて(逆)需要関数を導出するには、(N/100)Vi=Pとして、11.1式を代入すると、
(N/100)(10万100-100i)=P → N(1001-i)=P
ここで変数iは、購入者数Nと書き換えることができるので、(逆)需要関数は結局、
P=(1001-N)N ・・・11.2
興味深いことに、11.2式は「2次関数」となり、一般的に複数均衡となる(A点とB点)。

もし市場価格P=3万円だったときの需要量は、
3万=(1001-N)N → N^2-1001N+3万=0
という2次方程式を解いて、Na=30.925、Nb=970.07という2つの解が得られる。
複数均衡と来れば、均衡の安定性の問題である。
まず低位均衡のA点について。30人未満の場合、例えば1番目の人は、留保効用10万円なのだが、
ネットワーク外部性を考慮した効用は、次のように千円となり、市場価格3万円より低いので購入しない。
(N/100)Vi → (1/100)10万円=千円
ところが、もし30人がすでに購入していると、31人目の効用は、市場価格3万円より高いので購入する。
(31/100)×9万7千円=3万70円
32番目以降の人も、次々と同様の理由で購入していく。
このような現象を、皆が持っているので自分も買うという行動=バンドワゴン効果と呼ぶ。
ただし、潜在消費者1000人の全員が買うわけではないことに注意。
購入者が増えるほど、ネットワーク外部性は確かに大きくなるが、
一方で消費者の留保効用Viは、100円ずつ小さくなっていくので、
ネットワーク外部性を考慮した限界便益は、次第に頭打ちとなる。
さて、問題の均衡の安定性についてだが、何かの拍子にA点よりほんの少しでも左側が実現してしまうと、
購入者数はどんどん減り続けて、最終的にゼロとなる。
一方、A点以上になると、今度はどんどん購入者が増え続ける。
どちらも、どんどん離れて行くので、均衡点Aは不安定である。
この均衡点Aは、クリティカル・マスと呼ばれる(つまり臨界点)。
いったんクリティカル・マスを越えれば、雪だるま式に購入者が増えるので、独占市場になりやすい。
一方、高位均衡のB点の安定性はどうだろうか?
B点より左側のときには、人数がどんどん増えるのでB点に近づいていく。
しかしB点を越えると、ネットワーク外部性を考慮しても、市場価格>限界便益となって購入しない。
そのため、B点より右側では、人数がどんどん減るので、やっぱりB点に近づいて行く。
すなわち、均衡点Bは安定である。
何かの拍子にB点より左側や右側にちょっと動いてしまったとしても、また元のB点に戻る力が働くからだ。
・ まずはマーケットシェアの確保
市場価格P=1万円にすると、クリティカル・マス=10.092となるので、クリティカル・マスを越えやすくなる。
そこで各企業は、ネットワーク外部性のある財を売り出すときに、
その市場における自社製品の顧客数を確保するために、しばしば無料(や低価格)キャンペーンを行う。
市場の立ち上がり段階や、新規参入企業は、最初に売り出した時点でどれだけ顧客を確保できるかによって、
独占企業となれるか退出せざるを得ないかが決まってくる。
・ ネットワーク外部性と来れば、「標準化」
規格が統一(標準化)されていると、ハードウェア(機器)にしろ、ソフトウェアにしろ、
繋げやすかったり、互換性(置き換えやすい)があったりして便利ではある。
ソフトの互換性で思い付くのがPDF形式の文書ファイル。
しかし、一方で独占の弊害も発生し、特に過剰慣性(ロックイン効果)が、独占状態を存続させやすくする。
過剰慣性(ロックイン効果)とは、消費者が1つの規格やネットワーク・サービスに慣れ親しんでしまうと、
他の規格に切り替えにくくなるというもの。
切り替えるのに大変な心理的負担や、時間・労力が必要となるし、
例えばOSを変えるとなると、互換性のあるアプリケーションソフトまで換えなければならなくなり、
それまで持っていたソフト資産がすべて無駄となる。
このような費用を、スイッチング費用(転換費用)と呼ぶ。
スイッチング費用の存在が、過剰慣性(ロックイン効果)を生み、
その結果、より高い社会厚生を実現するような新技術や、品質の高いネットワーク財を供給しようとする企業の、
新規参入が困難となる。
かといって、政府の所轄官庁などの規制当局が、強制的に新規格を基準化するのも、なかなか難しいだろう。
・ 補完財(ヴァリアンの入ミク(9版)の36章「情報技術」より)
ネットワーク外部性とは定義的に異なるが、似たような問題を持つのが補完財。
靴は左足と右足の両方があって初めて役に立つ。
DVDソフトとDVDプレーヤー、CPUとOS、OSとアプリケーションソフトなど。
補完関係にある相手の財の価格が低下すれば、自分の収入(利潤)が増える。
ゲーム理論的状況(戦略的相互依存関係)になっていることが、この時点でわかる。
家電メーカーは、利用可能なコンテンツが十分に生産されると保証するまで、DVDプレーヤーを作りたがらないし、
逆にソフト会社は、DVDプレーヤーが十分に普及されるまで、コンテンツを作りたがらない。
合併するかどうかはともかく、結合利潤を最大化するように行動できれば、クリティカルマスを超えやすい。
また、規格を統一(標準化)することは、競争を激しくすることで、補完財の価格を下げる効果もある。
OSの会社から見れば、ハードウェアの規格が統一されれば、OSの生産が容易になるだけではなく、
ハードウェア産業に競争圧力を生む。
● コースの定理
http://jairo.nii.ac.jp/0047/00000352
コースの定理は本当に成立するのか (1)
http://jairo.nii.ac.jp/0047/00000319
コースの定理は本当に成立するのか (2)
同内容が次の教科書に載っていて、さらに上記ファイルには無い説明もある。
「中村竜哉 法と経済学 企業組織論に係る分析手法の研究 白桃書房 2010/12」
コースの定理というのはスティグラーが名付けたもので、コース自身ではない。一般的にコースの定理は、
1:権利の配分と、パレート効率的な資源配分(生産パターン)は無関係である。
ただし、所得分配には影響を与える。
ことを述べるものであるが、コース自身はそのような世界が現実に成り立つことを主張することが
目的だったわけではない。
2:現実には取引費用の存在から法制度が資源配分に影響を与える。
3:取引費用が大きすぎて市場取引が不可能な場合、外部性の問題は企業内取引(組織内)で解決される。
2と3の重要性を主張するのがコース自身の目的で、
経済学の分野では後々、2は法と経済学、3は組織の経済学へと発展する。
○ スティグラーの解釈(ファイル1の2.1、教科書の4章8節)
まずコースの定理を説明する時によく出てくる例として、工場とクリーニング店の例と、農場と牧場の例が有名。
前者は、工場の出す煙がクリーニング店の洗濯物を汚すという外部不経済の例。
後者は、先にある土地で農場を営んでいた隣に、牧場が出来た結果、
牛が隣の農作物を食い荒らしたという外部不経済の例。
どちらのケースも理不尽に思えるかもしれないが、権利配分を考えるということは、
逆に(先着順含めて)どちらも権利なしの状態から考察を始める。
例えば農場と牧場のケースでは、牧場の方が加害者と思ってしまうが、
どちらにも権利なしの世界では、牧場主の立場から見れば、勝手に牧草地を農場に変えられたとも言える。
次の表(ファイル1の表1、教科書の表4(p95)および表12(p142))の数値例を用いると、
「牛を1頭増やすごとの限界収入>農場の限界損害」である限り、牛は増やした方が社会的に効率的である。
牛の数 | 牧場主の収入の総額 | 農場主の損害の総額
──────────────────────────
9頭 | 94ドル | 0ドル
──────────────────────────
10 | 100 | 2
──────────────────────────
11 | 105 | 3
──────────────────────────
12 | 109 | 6
──────────────────────────
13 | 111 | 10
──────────────────────────
14 | 112 | 15
──────────────────────────
15 | 111 | 21
──────────────────────────
12頭→13頭にしたときの、
牧場の限界収入=111-109=3
農場の限界損害=10-6=4
となって、そこで初めて、牧場の限界収入<農場の限界損害となる。
社会的に見れば牧場の最適生産量は牛12頭である。
取引費用が0で、交渉が可能である限り、この最適生産量は変化しない。
牧場主が自分のことだけを考えれば、14頭までは限界収入が正なので、
14頭まで生産量を増やすことが最適なのではと思うかもしれないが、コースの定理ではそうならない。
交渉によって取引が行われるからだ。
権利の配分は、生産活動が終わった後の所得分配については影響を与えるが、
生産に関する条件である限界収入や限界損害には影響を与えない(需要の所得効果が0ならば)。
すなわち上記の表1そのものは、権利の配分によっては変化しない。
もし放牧の自由の権利を認めた場合は、農場に権利があるときと比べて確かに農場主の所得は減る。
しかし交渉による取引を考慮すると、権利は牧場側にあるので、農場の方が牧場に対して
生産量を減らしてくれと頼む形で交渉が行われる。
農場が牧場に14頭から13頭に減らしてくれと頼むと、牧場側で減る収入は112-111=1ドルなので、
1ドルを補償費用として支払えばいい。
その結果、農場側では損害額が15-10=5ドルも減る。差し引きで4ドルも損害額を減らせる。
一方、社会全体で効率的な水準である12頭の状態で、農場側はまだ6ドルの損害が出てるので、
さらに11頭に減らしてくれと牧場に頼んだ場合、それで減らせる農場側の損害額は
6-3=3ドルにしかならないが、牧場に支払う補償費用は109-105=4ドルになる。
逆に農場側に権利がある場合、今度は牧場側が農場に対して生産量を増やさせてくれと頼む形で交渉が行われる。
同じような類推(アナロジー)によって、最適生産量は結局12頭となる。
お互いの限界収入と限界損害を比較考量して、初めて社会全体の効率的な水準を導出できるのだ。
コースの定理は一見冷たいように思えるかもしれない。
しかし、もし農場主と牧場主が結婚したらと考えれば何も心理的抵抗はない。
そこで結合利潤を考えることが、効率的水準を明らかにすることを、下記の生産の外部性で説明する。
○ まずは消費の外部性とコースの定理を、林公共の説明で紹介
https://sites.google.com/site/publicfinanceuoftokyo/toppage/public-finance-law
で、公開されている林先生のノートの、ファイル07の図4-1。教科書では4章。

喫煙家Aと嫌煙家Bの例で、AがBに外部不経済を与えている。タバコの消費量=Z、タバコの価格=p。
Aの限界便益=限界便益MB(Z)
Bの限界損害(限界外部費用)=MD(Z)
Aの(純)限界便益:限界便益MB(Z)-p
Aにとっての私的限界費用=p
社会的限界費用=p+MD(Z)
パレート効率的なのは、pを原点と考えて、MB(Z)とp+MD(Z)の交点Cで、最適消費量=Z*。
そのとき、Aの純便益CD=Bの限界損害FZ*、になる。
ケース1:Aに喫煙権がある場合、MB(Z)=pとなる消費量Zバー(Z*以上の過剰消費量)となる。
ケース2:Bにきれいな空気を吸う権利がある場合は、Z=0となる。
消費量は権利の配分で変化しているように見える。
ところが、ケース1ではBがAに補償してZを減らしてもらえば、
Z*より右側ではCD<FZ*なので、補償費用CD以上に限界損害が減るのでBにとって得となる。
ケース2では、AがBに吸わせて欲しいと補償すれば、
Z*より左側ではCD>FZ*なので、補償費用FZ*以上に限界便益が増えるのでAにとって得となる。
純粋交換経済のエッジワースボックスを思い出そう。外部性がなければ市場価格だけを見て、
分権的に意思決定するだけで、後は取引(交渉)を通じて勝手にパレート効率的になる。
逆に、消費の外部性(市場取引を通じずに効果が市場の外に及ぶ)があると、パレート効率的にならない。
外部性があるというのはその外部効果を取引する市場がないということであり、
それは所有権が設定されていないことを意味する。喫煙の例で言えば、空気の所有権を設定するのは不可能に近い。
所有権が無ければ、取引だって発生しないのは自明である。
みんなが他人の持ってる物も俺の物だと思ってるジャイアンになる。
しかし、所有権さえ確定されれば、たとえ外部性があっても、後は取引(交渉)を通じて内部化される。
それこそがコースの定理の本質なのである。そしてその権利をどちらに配分しようと結果は同じになる。
パレート効率的水準(資源配分)は不変となる。
ただし、資源配分には影響を与えなくても、所得分配の結果には影響を与える。
例えばケース1の方が、Aにとって所得分配の結果は有利であるから、喫煙権を主張するだろう。
図4-1はコースの定理を説明するときによく用いられる図だが、成立するためには条件が必要で、
条件1:取引費用が小さくて交渉可能
条件2:需要の所得効果がゼロ(すなわち準線形効用関数を仮定)
準線形効用関数(準線形選好)については、 ミクロ経済学ノートを参照。
所得効果が存在すると、補償を支払った時点で、MB(Z)やMD(Z)そのものがシフトしてしまう。
そのため、パレート効率的水準(Z*)そのものが定まらない。
さらに林公共や柴田公共では、コースの定理も柴田のダイアグラムを使って説明している。
林公共の図4-10(本ノートの林公共の章を参照)では、2つのレンズが描かれている。
AとBのどちらに権利を配分するかによって、レンズ内で成立するパレート効率的水準は
Z1~Z2の範囲か、Z3~Z4の範囲に別れる。
AとBの無差別曲線同士が接する契約曲線KK’は斜めになっているが、
もし需要の所得効果が無ければ、契約曲線KK’は垂直となり、最適消費量Z*は1つに決まる。
○ ヴァリアンの入ミク(9版)の35章「外部性」から、生産の外部性
川上の工場Sが、川に汚染水xを流すことで、川下の漁場Fに外部被害(外部不経済)を与えているとしよう。
工場の生産量をs、漁師の生産量をf、
工場Sの費用関数をCs(s,x)、漁師の費用関数をCf(f,x)、
∂Cs/∂x<0、∂Cf/∂x>0とする。
工場Sから見て、汚染水xを川に流した方が費用を節約でき、逆に汚染水を川に流さないようにするには、
余計な費用が掛かることを意味する。
・ 権利が確定しておらず、工場Sが汚染水を勝手に川に流すケース1
工場Sの利潤関数:Ps・s-Cs(s,x)
漁師Fの利潤関数:Pf・f-Cf(f,x)
汚染水xは工場がコントロールするので、それぞれの利潤最大化条件は、
工場Sの利潤最大化条件:Ps=∂Cs/∂s と 0=∂Cs/∂x
漁師Fの利潤最大化条件:Pf=∂Cf/∂f
工場Sは汚染水の限界費用が0になるまで川に垂れ流し、漁師Fはそれを見ていることしかできない。
∂Cf/∂x>0なのだが、工場Sは無視している。社会的限界費用が考慮されておらず過剰生産。
・ 合併して結合利潤を考えるケース2
結合利潤:Ps・s+Pf・f-Cs(s,x)-Cf(f,x)
利潤最大化条件は、操作変数がs、f、xの3種類なので、
Ps=∂Cs/∂s
Pf=∂Cf/∂f
∂Cs/∂x+∂Cf/∂x=0 → -∂Cs/∂x=∂Cf/∂x
3本目の式が重要で、ちゃんと漁師への限界被害∂Cf/∂xを考慮に入れている。
両者に発生する限界費用の和=社会的限界費用が考慮されており、パレート効率的である。
・ 権利が確定しており、漁師Fが川を汚染されない権利を持つ。xを1単位、qの価格で取引できるケース3
工場Sの利潤関数:Ps・s-qx-Cs(s,x)
漁師Fの利潤関数:Pf・f+qx-Cf(f,x)
漁師の方もxの権利を何単位売るかコントロールできるので、利潤最大化条件は、
工場Sの利潤最大化条件:Ps=∂Cs/∂s と q=-∂Cs/∂x
漁師Fの利潤最大化条件:Pf=∂Cf/∂f と q=∂Cf/∂x
ケース2と同じ結果となる。
・ 権利が確定しており、工場Sがx#だけ放流できる権利を持つ。xを1単位、qの価格で取引できるケース4
ちょっと複雑になる。
工場Sの利潤関数:Ps・s+q(x#-x)-Cs(s,x)
漁師Fの利潤関数:Pf・f-q(x#-x)-Cf(f,x)
工場Sにとって放流できるのはx#までなので、それを超えるxは漁師Fに補償することになる。利潤最大化条件は、
工場Sの利潤最大化条件:Ps=∂Cs/∂s と q=-∂Cs/∂x
漁師Fの利潤最大化条件:Pf=∂Cf/∂f と q=∂Cf/∂x
ケース2およびケース3と同じ結果になる。すなわち授権方法と最適生産量は無関係で、
パレート効率的な資源配分の水準は不変というコースの定理。
・ 35章5節「市場シグナル」
合併すれば結合利潤は最大化される。ということは、もし合併していなければ、利潤の合計は結合利潤より低くなり、
必ず買収圧力が働く。買収しようとするのが誰であれ、買収すれば必ず儲かるからだ。
従って利潤最大化というインセンティブによって、ほっとけば勝手に外部性は内部化される。
○ レントと準レント
ミクロ経済学ノートを参照。
○ ファイル1の3.1節、教科書の5章4節
小麦の生産量=w
牛肉の生産量=m
小麦の価格=5
牛肉の価格=10
小麦の費用関数:Cw=0.5w(1+w)
牛肉の費用関数:Cm=0.5m(11+m)
小麦への損害「量」(額ではないことに注意)をdとすると、
d=0.1mw
牛の量が一定でも、小麦が増えれば小麦への損害量自体は増えるという関係を意味する。
では、共同経営による結合利潤を考えよう。損害「額」=5×d=0.5mwであることに注意すると、
結合利潤π=πw+πm-5d ・・・1
=5w-Cw + 10m-Cm - 0.5mw
結合利潤を最大化する小麦と牛肉の最適生産量は、
∂π/∂w=5-0.5-w-0.5m=0 ・・・2A
∂π/∂m=10-5.5-m-0.5w=0 ・・・2B
内生変数2個で、方程式が2本なので解が求まる。結果、w=3と、m=3になる。
結合利潤=総収入-総費用-小麦の損害額
総収入=3×5ドル+3×10ドル=45ドル
総費用=(0.5×3×4)+(0.5×3×14)=6+21=27ドル
小麦の損害額=5ドル×0.1×3×3=4.5ドル
共同経営で発生する結合利潤は、13.5ドルである。
最適生産量のw=3と、m=3から、wやmをどう変化させても結合利潤は減ってしまうことを確認してみよう。
そこでもし小麦と牛肉が異なる経営者によって個別に経営された場合、
農場に権利を付与すると、最適生産量が変わるかどうかを調べてみよう。
例えば農場が損害額について、どうせ賠償してもらえると思って気にせず利潤最大化を行うと、
∂πw/∂w=5-0.5-w=0 → w=4.5
農場の利潤=5ドル×4.5-0.5×4.5×5.5=22.5-12.375=10.125 ・・・3
これだけを見ると、権利が農場に付与されれば、農場は生産量を増やしそうに見える。
ところが、損害賠償責任を考慮に入れた牧場が利潤最大化を行うと、
πm♯=πm+5d
∂πm♯/∂m=10-5.5-m-0.5w=0 ・・・4
w=4.5を所与とせざるを得ないので、4式に代入すると、
m=2.25
牧場の利潤=10ドル×2.25-0.5×2.25×13.25-5×0.1×4.5×2.25
=22.5-14.90625-5.0625=2.53125 ・・・5
農場の利潤と合計しても、13.5ドル未満となってしまう。
こうなると、どういう交渉が起きるだろうか?
小麦の生産量を4.5から3へ減らしてくれと牧場主が頼むと、
農場の利潤は9ドルとなって1.125ドル減る。
しかし牧場はその分、4式においてm=3にできて、利潤は30-21-4.5=4.5ドルになる。
すなわち牧場の利潤は1.96875ドル増える。
そうすると、農場の減った利潤1.125ドルを補償して、
まだ牧場主には0.84375ドルの利潤の増加が見込める。
結合利潤がw=3と、m=3のとき最大であるということは、
それ以外の生産量を選んでる状態から、最適生産量にすることで必ず補償ができるのだ。
結局、農場に権利を付与した場合、結合利潤の最大化において、wで偏微分した時だけ、
損害額(5d)を認識しないことを意味するので、
∂π/∂w=5-0.5-w=0 ・・・2A’
∂π/∂m=10-5.5-m-0.5w=0 ・・・2B
となることを意味する。しかしこれは結合利潤を最大化する条件とは異なる。
共同経営で発生する結合利潤は、13.5ドルが最大なのだから、
2B式はともかく2A’式のような最適化では必ずそれ以下になる。
だったら、交渉によって最適生産量より低い方が、最適生産量より多い方に減らすように頼めば、
多い方で減った利潤を、低い方で増えた利潤で必ず補償できる。
結合利潤=総収入-総費用-小麦の損害額
という式自体は、権利の付与の仕方に関わらず不変なので、
共同経営じゃなくても取引費用がゼロで交渉が可能であれば、これを最大化する最適生産量が必ず実現できる。
これまでの結果を、今度は牧場に権利を付与した場合について考察してみよう。
今度は牧場主が損害額(5d)を認識しないので、結局、
∂π/∂w=5-0.5-w-0.5m=0 ・・・2A
∂π/∂m=10-5.5-m=0 ・・・2B’
2B’式から、m=4.5となる。
牧場の利潤=10ドル×4.5-0.5×4.5×15.5=45-34.875=10.125
農家はm=4.5を所与とせざるを得ないので、2A式より、w=2.25
農場の利潤=5ドル×2.25-0.5×2.25×3.25-0.5×2.25×4.5
=11.25-3.65625-5.0625=2.53125
農場に権利があったケースに対して、見事に数値が対称となっている。
農家が牧場主に対して牛肉の生産量を4.5から3に減らしてくれと頼めば、
牧場主の利潤はやはり同じ9ドルとなり、1.125ドル減る。
一方、農家が小麦の生産量を3に増やせば、こちらも見事に利潤は4.5ドルになり、
利潤は1.96875ドル増えるので、補償できる。
○ コースの定理が成り立つ条件、成り立たない条件。
さて、取引費用がゼロで交渉が可能であれば、権利の付与に関係なく「必ず」最適生産量になると言ったが、
実はかなり特殊な数値例の下でのみ成立する。
もし違う数値例であれば、成立しないのである(D.L.Shapiro [1974])。
それぞれの総費用関数を次のような数値例に変えてみる(7という固定費用を追加)。
小麦の費用関数:Cw=7+0.5w(1+w)
牛肉の費用関数:Cm=7+0.5m(11+m)
後は結合利潤の式を作って、mとwで偏微分してそれぞれの最適生産量を求めてみると、
追加された「+7」の部分は偏微分の過程で消えるので、最適生産量は相変わらず、w=3と、m=3である。
総収入は相変わらず45ドルであり、小麦の損害額も4.5ドルのままであるが、
総費用が27ドルから41ドルに増える(その差は14)。
結果、結合利潤は最適生産量であっても-0.5ドルとなる。
最大でマイナスなのだから、最適じゃない生産量から最適な生産量に変化させることで
増える利潤で補償費用を賄うなんてどちらにしろ不可能である。
つまり、コースの定理はもはや成り立たない。結局、外部不経済(ここでは小麦の損害額の5d)を
カバーする(内部化する)利潤や所得を生み出している条件の下でのみ、コースの定理は成立するのである。
補償するということは、相手の持っている権利を購入していることに他ならないわけで、
権利という財を買うときには、予算制約に縛られる。
資源配分が不変どころか、そもそもパレート効率的水準すら達成できない。

林公共の図4-10で言えば、Aにタバコを吸う権利があるF点から出発して、
タバコの煙に対する需要の所得効果が0で、例えば契約曲線KK’がZ3の水準で垂直だったとしよう。
_ _
Aの無差別曲線VAに沿って、Zから出発して左のZ3までAに移動してもらうには、
Aの予算制約線であるHJ線からκ点までの垂直距離の分だけ、Bが補償しなければならない。
ところが、Bの所得(線分OBH)がその垂直距離より短いと、所得を全額使って補償しても、Z3まで移動できない。
それでも、パレート改善できるレンズ内の色が付いた部分が、まだあるかもしれない。
Z3までは行けなくても、少なくともZバーよりは左に行けるかもしれない。
しかし、それは契約曲線上ではないので、パレート効率的とは言えない。
柴田公共の所でも話したが、忘れがちだけど重要な問題なのが、端点解のケースである。
また、Regan(1972)が指摘するように、長期的には準レントは0となり、生産要素に対する機会費用を
稼ぎ出すだけとなる(長期的に経済学的な利潤は0となるので、補償する余裕などない)。
○ ファイル1の3.1節に無い説明を、教科書から紹介(p135~p138と表10)
Coase(1988)は次のようなケース(表10)を用いて、コースの定理が成り立つと反論している。
まず準レント(財市場の生産者余剰)ではなく、農家と牧場主のレント(生産要素市場の生産者余剰)を用いる。
農家のレント:a
牧場主のレント:b
被害額:c
ケース1:農家の稼ぎ出すレントを100ドル、牧場主のレントも100ドル、被害額を50ドルとしよう。
牧場主に損害賠償責任がある場合、レントから50ドルを支払って、まだ操業を続けるだろう。合計は150ドル。
責任が無い場合、農家のレントが50ドルとなって、まだ操業を続けるので、資源配分は不変。合計は150ドル。
ちょっと飛んでケース4:農家のレントは30ドル、牧場主のレントは40ドル、被害額は50ドルのまま。
牧場主に損害賠償責任がある場合、賠償をするより農家に30ドル払って操業を辞めてもらった方が安くつく。
牧場のみが操業し続けて、農家は働かずに30ドルを得て、牧場は10ドルとなり、合計40ドル。
責任が無い場合、農家は被害額がレントを上回るので操業停止し、牧場のみが操業。資源配分は同じ。合計40ドル。
ケース5:農家のレントは40ドル、牧場主のレントは30ドル、被害額を50ドル。
農家と牧場主の立場がケース4と逆になる。資源配分は同じで、合計40ドル。
特に(5,なし)のケースでは、今度は農家の方が牧場を買収する。
表10 ─────────────────────────
│ 牧場主に責任あり │ 牧場主に責任なし │
────────────────────────────────
│a=100│ 双方が操業を続ける │ 双方が操業を続ける │
1│b=100│農家100、牧場主50│農家50、牧場主100│
│c=50 │ 合計150 │ 合計150 │
────────────────────────────────
│a=25 │牧場のみが操業を続ける│牧場のみが操業を続ける│
2│b=100│ 農家25、牧場主75│ 農家0、牧場主100│
│c=50 │ 合計100 │ 合計100 │
────────────────────────────────
│a=100│農家のみが操業を続ける│農家のみが操業を続ける│
3│b=25 │ 農家100、牧場主0│ 農家75、牧場主25│
│c=50 │ 合計100 │ 合計100 │
────────────────────────────────
│a=30 │牧場のみが操業を続ける│牧場のみが操業を続ける│
4│b=40 │ 農家30、牧場主10│ 農家0、牧場主40 │
│c=50 │ 合計40 │ 合計40 │
────────────────────────────────
│a=40 │農家のみが操業を続ける│農家のみが操業を続ける│
5│b=30 │ 農家40、牧場主0 │ 農家10、牧場主30│
│c=50 │ 合計40 │ 合計40 │
────────────────────────────────
(3,なし)のケースでは、農家が牧場主に25ドル渡して操業を停止してもらう。これは理解できるが、
(2,あり)のケースでは、牧場主の損害賠償額は25ドルで、農家は操業停止と説明している。
たぶん、牛の潜在能力はMAXで50ドル分の農作物を食い荒らせるが、そもそも25ドル分の農作物しかないので、
損害賠償は25ドルでいいということか。
さて、ケース4と5は、損害賠償に関してはレントが足りないので不可能だが、相変わらず相手を買収できている。
予算制約に縛られて(予算制約がバインドして)いないケースを持ち出しており、反論になってないと思う。
例えば表10の(4,あり)のケース。他の仕事(漁業)のレントが30だったとしよう。
農家を買収しつつ牧場で働けばレントは10ドルだが、牧場主はそれでも農家を買収するのだろうか?
あるいは、お互いのレントが30だったらどうするのだろうか?
牧場主に責任ありの場合、牧場主は働いて稼いだ30ドルで農家を買収し、最終的にレントは0ドル。
農家は働かずに30ドル・・・。しかも牧場主は毎月・毎年農家にレントを払わなければならない。
面白いのが、表を縦に見ること。一見この表では、権利配分によって資源配分は変化していない。
ケース4で横に見れば、牧場主の責任の有無によって、どちらも牧場のみが操業しているし、
ケース5で横に見れば、権利配分によらず、農家のみが操業している。
ところが、(4,あり)のケースと、(5,あり)のケースを比べてみよう。
権利配分は同じだが、農家と牧場主のレントが違う。すなわち、所得分配が変化すると資源配分も変化する。
牧場のみ操業→農家のみ操業となっている。そこで需要の所得効果0の話に移ろう。
○ 所得効果(富効果)。ファイル1の3.2、教科書の5章5節。
これに関しては、林公共の所で散々説明しているので、コースによる反論をいきなり紹介しよう。
Coase(1988)による反論は、ファイルの方には無く、教科書の方にしかない。
さまよえる牛のケースを用いよう。Demsetz(1972)によると、例えば農家は小麦で作られたパンの方が好きで、
牧場主は牛肉の方が好きだとしよう。
そこで権利配分が農家に有利となれば、農家の所得が増えて牧場主の所得が減る。
小麦の需要は増えて価格は上昇し、牛肉の需要は減って価格は下落するだろう。
すなわち、権利配分によって所得分配が変化したとき、牛肉や小麦に対する需要と価格が変化する可能性があり、
さまよえる牛のケースの表(限界収入および限界損害)そのものが変化してしまうのだ。
コースによる反論は、農家と牧場主の両者とも、土地は自己所有ではなく、借地とする。
そして両方の土地は、1人の地主によって所有されているとしよう。
この場合、牛肉と小麦に対する需要および価格の変化は、そのまま土地の均衡賃貸料に反映され、
農家の賃貸料は上昇し、牧場主の賃貸料は下落するので、両者の所得分配は変化せず、地主の所得も変化しない。
地主が1人なおかげで、農場と牧場は間接的に共同所有しているような形になっているので、
両者の間で発生した所得分配の変化は、相殺されることになる。
しかしこのコースの反論の仕方も、前節と同様に反論になってないと思う。
需要の所得効果が0じゃない状態で、所得分配が変化したらどうなるか?と聞いているのに、
そもそも最初から所得分配が変化しないケースを持ち出すのは、本末転倒である。
コースに対する再反論は、地主が別々だったら?で終わりな気がする。
牧場の地主は牛肉が好きで、農場の地主はパンが好きで・・・。
あるいは賃貸料の下がった牧場には貸さず、マンションを建てるかもしれない。
そもそもコース自身、前節の表10で、所得分配の違いで資源配分が違うことを説明している。
○ ファイル1の3.3、教科書の5章7節、「参入・退出の自由」
最初はAに責任が割り当てられている状態から、ルール変更によってBに責任が割り当てられたとしよう。
BがAに生産量を減らしてくれと頼む形で交渉が行われ、変更後にAの利潤は増えて、Bの利潤は減る。
法と経済学ノートに頻繁に出てくる、 Carabresi(1965)よると、(上記の漁業の例のように)機会費用を考えた場合、
他の産業における生産要素の収益率は均等化するので、
(生産のパレート効率性の話で、例えばX財産業とY財産業と労働市場の均衡を考えると、
Px・MPLx=W=Py・MPLyとなる)
長期的にAの産業には参入が、Bの産業では退出が起きて、資源配分は変化し、コースの定理は不成立。
Zerbe(1976)(1980)によると、そのような批判は間違っていて、
ルール変化前はAの支払う損害賠償金が限界費用に含まれており、変化後にはAが生産拡大を諦める代わりに、
受け取る損害賠償金が含まれるので、利潤が増減することは無いらしい。
ちょっと分からない。ファイル1の3.1節、教科書の5章4節の、小麦と牛肉の数値例によると、
どう考えても利潤は変化している。
○ ファイル2の3.6.2、教科書の5章10節2項、「財産権ルールとコスト関数」
これの1つ前の、ファイル2の3.6.1、教科書の5章10節1項の最後より、
取引費用と所得効果が無いケースを引き続き扱っている。
Aが被害企業、Bが加害企業とする。Frech(1979)によると、BがAに損害賠償責任があるルールと、
Aに外部性を発生させない所有権(財産権)があるルールとでは、結論が異なる。
法律上の責任ルールだと、短期においては(交渉によって)コースの定理は成立するが、
参入・退出がある長期においては、不成立となる。
ところが、所有権ルールならば、参入・退出がある長期においても、コースの定理は成立する。
ファイルの方も教科書の方も、説明が少なすぎて理解できなかった。
ファイルと教科書の双方とも式番号は同じで、5~8式の内、5式と6式は生産量のaとbでラグランジュ関数を
偏微分すれば導出できる。7式と8式は長期における参入と退出を考慮するので、企業数のnaとnbで
ラグランジュ関数を偏微分すれば導出できる。
それ以降がどういう設定なのか理解できない。特に財産権ルールの第4。
「参入企業にとって参入価格は均衡において限界費用に等しく、他に転嫁できないので限界費用は0となる。」
どういうことなのか分からないが、少し戻ってファイル1の3.3、教科書の5章7節の最後より、
結局は所有権ルールの下でも、所得効果がある場合、コースの定理は長期(参入・退出)においても不成立。
● 最後に回しておいた、林公共の10章と12章。
○ 10章、公的扶助と効率的な再分配。
個人的に林公共の中で一番好きな章で、給付の具体的な方法を詳しく検討している。
これまで、他の教科書を読んでいるときには、負の所得税はかなり性質が良くて、
なんで現実の世界でどこの国もやらないのだろうとずっと疑問を持っていたが、
本書で強調されている説明でやっと理由が分かった。
負の所得税は課税最低限以下の所得の人達に対して給付を行う(ベーシックインカムだと国民全員になる)。
これはちょっと考えただけでも、ものすごい給付総額になる。
財源をいったん確保する過程で、徴税コストや税率が影響を与える資源配分の歪みなどが、かなり大きくなる。
そこで次に考えられるのが、給付が本当に必要な低所得者層に限定する方法で、それなら財源確保も少なくて済む。
カテゴリーに分類してターゲットだけに給付を行うことをタギング(札貼り)という。
ところが今度はターゲット効率性という問題が生じる。
例えば低所得を基準にタギングを行うと、本当は働けるのにあえて働かず、給付を受けようとする者が現れる。
個人がそのように操作できるような基準でタギングを行うのは望ましくない。
本来、給付の対象となるべき層は、所得が低い人達ではなく、
障害者や母子家庭などの所得を獲得する能力が低い人達であろう。
所得だけを基準にしてしまうと、能力の高い人まで不正受給してしまう可能性がある。
獲得能力の高い人は、短い労働時間で高い所得を獲得でき、
低い能力の人が同じ所得を得るためには長時間労働が必要となる。
・ 10章4節、情報の非対称性。
タギングの効率性を高める上で問題となるのが、情報の非対称性である。
本来、基準とすべき所得獲得能力は、観察するにはかなり難しい。そこで所得を基準にせざるを得ない。
その前に、どういう記号を定義し、どういう図を描き、それをどう説明するかについて、
本書の10章はちょっと難しい。
よーく読んで記号や変数の意味を理解して、図とにらめっこしながら、慎重に何度も読まないと理解できない。
まず能力の高いAと低いBについて、効用関数には労働時間Hも負効用として入る。消費量をCとする。
効用関数はU=U(C,H)。
賃金率をWとすると、Y=WHとなるので、H=Y/Wとできる。
賃金率Wは個人にとって選択できず所与だが、能力の違いによりWa>Wb。
所得の高いAに税金T、それをBに所得移転。
可処分所得で消費するので、最終的に効用関数は変数Yだけで表現でき、
Ua=U(Ya-T,Ya/Wa) Ub=U(Yb+T,Yb/Wb)
タギングの方法1:所得制限
仮定1:同一の効用関数
仮定2:情報の非対称性から確認できるのは所得だけ。
Bの効用を最大化する所得をYb*、 _
給付が受け取れるか受け取れないかの基準となる所得制限をY(以下、Yバー)とする。
情報の非対称性から、Aは自分の所得をYバーに偽る。 Λ
そこで、Aの偽る前の効用関数をUa、偽ったときの効用関数をUa(以下、Uaハット)とする。

教科書のP307、講義ノートの方はファイル13、それぞれにある図10-7を見ると、
まずYバー=Yb*と設定してみて、横軸上のYバー=Yb*の水準で垂線を描くと、
まずUbの最高点にぶつかり(B点)、さらにその上の方でUaハットとぶつかる(A点)。
効用関数UaハットがUbの上方に位置する理由は、後で説明する。
Bにとって給付が受け取れて、なおかつBの効用水準が一番高いのはYb*なので、
政策当局はBのことだけを考えて、Yバー=Yb*とするのが望ましいように見えるかもしれない。
しかしB点でのBの効用関数は、効用最大化水準に位置するので、傾きはゼロ=平らである一方、
A点でのAの偽った効用関数は全然平らではなく、傾きはかなり急である。
そうすると、ほんの少し所得制限YバーをYb*より下げても、Bにとってはそんなに効用は減らないが、
偽っているAの効用は大きく下がる。
ここからがややこしいのだが、議論しやすいために、偽ってないときのAの効用最大化点をGとし、
たまたま、A=Gと同じ高さ(同じ効用水準)だったとしてみよう。
(同一の効用関数なのに、UbよりUaの方が右上に位置する理由も後で説明する。)
もしYバーをYb*より下げてみると、それに対応してA点からA’点に大きく下がり、Gの方が高くなるので、
Aは偽って働かないよりも、ちゃんと働くことを自ら選ぶ。
そこで出てくるのが自己選択制約式(グーグルで検索してみると、誘引両立制約と同じようだ)。
Λ _ _
Ua=U(Y+T,Y/Wa)≦U(Ya-T,Ya/Wa)=Ua ・・・1
1式の意味の前に、そもそもグラフ上で、偽ってる効用関数Uaハットが、
偽ってないUaよりも上方に位置している理由について。
偽っているUaハットは給付をもらっている一方で、偽ってないUaなんて、給付をもらえないどころか、
逆に税金を払っているので尚更だ。
もちろんUaハットはUbと比べても位置が高い。
Aが労働時間を減らして所得を偽っていても、賃金率がWa>Wbなので、
Bと同じ所得を得る上でBよりも少ない労働時間で済み、効用関数の中の労働の負効用がBよりも小さいため。
以上を踏まえれば、同質の効用関数でもUaがUbより右上に位置する理由もわかるだろう。
結局、図10-7は、横軸に所得Yを取って、効用関数を描いているので、
税金Tや、それぞれの賃金率WaとWbがパラメータとなる。
U字型になるのは、いずれ労働の不効用の方が上回るようになるから。
さて、1式が成り立つということは、どういう意味なのかを説明しよう。
働く時間を減らして偽ったときの効用(左辺)より、偽らずに長時間働いた方(右辺)が、
前者は給付がもらえて、後者は税金を払わなければならないとしても、それでも後者の方が効用が高いことを意味する。
もし1式が成り立てば、Aは自ら後者を選ぶということだ。
1式を外から制約条件として課しているので、自己選択制約式(誘因両立制約式)という。
YバーがYb*より下がれば、Bが給付を受け取るためには、少し労働時間を減らさなければならない。
そこだけ見れば、それはBにとって最適ではないように見えるかもしれない。
しかし、情報の非対称性が存在する世界では、基準となる所得制限Yバーをあえて少しを下げてやった方が、
その分Aが偽らずに働くインセンティブ(誘因)を持つようになり、
その結果、税収も増えるので、かえってBにとっても厚生を高められるのである。
Yバー=Yb*と設定したときには、A=Gとなっているので、1式が等号で結ばれる(Uaハット=Ua)。
Yバー<Yb*と設定したときには、1式が強い不等号(Uaハット<Ua)になる。
図10-7の縦軸上の記号で言えば、Ua’<Ua*となる。
1式の自己選択制約式が、前者ではもうギチギチの一杯だが、
後者は緩んでいるので、その分だけ課税Tを増やしてもAは偽らずに働き続ける。
タギングの方法2:現物給付
仮定1’:効用関数の異質性。方法1の仮定のうち、仮定1を変えて、効用関数は違うとする。
仮定2:方法1と同様に、情報の非対称性から確認できるのは所得だけ。
_ _
ここでも所得制限はY、BはY+給付Tを用いてX財を消費する。
そこで方法1のときとは違って、今度は横軸をXとする。縦軸は効用Uのまま。

図10-8では、Bの効用関数と、偽ったAの効用関数Uaハットだけを描いている。
それぞれの効用最大化水準では、Xa*ハット<Xb*となるとしよう。
Aについては、偽ったときだけを描いているのでハットも付く。
能力の低いBの方がたくさん消費するような財の例として、低質な住宅などを想定してみると分かりやすい。
_
ここでTの一部を現金ではなく、X財の現物給付としてみよう。その量をX(以下、Xバー)とすると、
給付全体のうち、現金部分はT-Xバーになる。
1:Xバー<Xa*ハットの場合
偽ってるAですら、まだXバー以上にX財を欲しいと思っているので、
現金給付部分を使ってさらにX財を購入しようとする。
このようなXバーの設定は、両者に何の影響も与えない。
2:Xa*ハット<Xバー<Xb*の場合
この領域では、偽ってるAの効用関数Uaハットは右下がり、Bの効用関数は右上がりとなるので、
Xバーの設定をこの領域になるように上げてやると、偽ってるAの効用は下げつつ、Bの効用は上がる。
3:Xb*<Xバーの場合
一見すると、Xバーの設定をBの効用最大化水準「以上」にしてしまってるので、
Bの効用を下げちゃうので良くないように思える。
しかし方法1のときと同じように、Bの効用減は微小に過ぎない一方、Aの効用減はかなり大きい。
描いてはいないが、もし偽っていないときの真のAの効用最大化水準Ua*(*は付くけどハットは付かない)
と比べて、Aの効用水準が大幅に下がってしまうぐらいまでXバーの設定を上げてやれば、
Aは自己選択制約によって自ら偽らなくなる。
すなわち、Bにとって最適となる以上に現物給付すると、
Aが不正受給をせずにちゃんと働いて税金を払うようになり、給付が本当に必要なBにとっても望ましい。
タギングの方法3:さらに所得も確認できないとき。
方法2では、Xバーという設定が出てきたが、相変わらず所得制限Yバーを基準として先に用いている。
従って、Aが不正受給するためには、労働時間を減らして所得を低く偽る必要があった。
ところが、所得獲得能力はだけじゃなく、所得水準も確認できない場合、
所得制限の設定を用いた不正受給が防止できない。
このケースも、給付の一部を現物給付とするのが効果的となる。しかもその現物給付は、必ず消費しなければならない。
住宅サービスを例に取り、低質住宅が下級財(所得が増えるとかえって消費量が減る財)であるとしよう。
高所得者が不正受給しても、低質住宅に住まなければならない場合、かえって効用は低下するので、
これまでの議論と同様に、不正受給を自らやめる。
しかも、住宅をさらに低質にすれば、より多くの不正受給者を締め出すことができる。
本来、給付を受け取るべき能力の低い人達にとっても効用は下がるが、その下がり方は小さいので、
トータルではかえって厚生が高まる。
P313の上から6行目、「方法1の場合、所得制限が余暇消費を制限している」という文章の意味について。
最初に読んだときは意味がわからなかったが、
方法1の場合、所得制限をさらに下げていけば、Aが偽って働かない(余暇を消費する)ことの効用減は大きく、
余暇消費を制限する=働かせるという意味。
・ 10章5節、利他主義。
意外と面白かった。というのも、利他主義であってもそれが複数いると問題が発生する。
・高所得者をA、低所得者をCとし、高所得者だけ利他主義とする。
・Aの効用関数は、Ua=U(Xa,Uc)
・Cの効用関数は、Uc=U(Xc)
・代入すると、Ua=U(Xa,U(Xc))となるので、結局、変数XaとXcの関数として、U(Xa,Xc)と表現できる。
すなわち、Xa-Xc平面に無差別曲線が描ける。
無差別曲線と来れば予算制約線なので、
・単純化してCの所得はゼロ
・Aからの移転所得をga
・Cの消費は、ga=Xc
・Aの予算制約式は、Ya=Xa+ga=Xa+Xc
この時点ではまだ問題ではない。問題が発生するのはここからで、もう1人の高所得な利他主義者Bがいると、
・Bの効用関数は、Ub=U(Xb,Xc)
・Bからの移転所得をgb
・Cの消費は、ga+gb=Xc
Cの予算制約式を、AとBのそれぞれの効用関数に代入すると、
・Ua=U(Xa,ga+gb)
・Ub=U(Xb,ga+gb)
・ga+gb=Xc
これはもはや、公共財の(相対)価格が、p=1のときの自発的供給(拠出均衡)の問題と同じ構造となる。
AとBはお互いに相手が出してくれることを期待してフリーライダーとなり、
パレート非効率的な水準となる(過少供給となる)。
従って、AもBも利他主義者にも関わらず、公的部門の介入がパレート改善に必要となる(本当にジレンマだな)。
また拠出均衡と同じ5章4節のクラウディングアウトで説明したように、
定額の固定税で政府が所得移転すると、同額だけAとBは自身の所得移転を減らす。
課税を定率にして、所得移転は定率補助にする必要がある。
・ 10章6節、サマリア人のジレンマ(サマリアびと、と読むらしい)。
そもそも10章は全体として、公的扶助とその効率性を分析する章である。
そこで6節では、動学的不整合性を検討する。
すなわち、公的部門が効率性を考えて、困窮者にできる限り自助努力をさせたくて、
困ってても助けないと宣言しても、その助けないという約束に法的拘束力や強制・義務がない限りは、
実際に困窮者が発生すれば、やっぱり助けた方が公的部門にとっても厚生が高い。
従って、困窮者はどうせ助けてくれるだろうと期待して、自助努力を行わない。
そのような口約束は、ゲーム理論的に言えば、部分ゲーム完全均衡ではなく、
信憑性のない脅し・コミット(宣言)となる。
動学的不整合性とは、事前に最適である戦略が、事後的には最適ではなくなること。
貯蓄と年金がいい例で、老年期に所得が無くて困るようなら、若年期に貯蓄しておいて欲しいと思って、
公的部門が老年期の困窮者は助けないと宣言しても、そのような戦略は公的部門にとって事後的に最適ではない。
それを見込んだ人々は、必ず救済されると期待して、若年期に貯蓄するより散財してしまうことになる。
このような動学的不整合性の対処法として、法的拘束力のあるコミットや、法的な強制・義務である。
貯蓄の例で言えば、強制的に社会保険料を徴収し、強制的に貯蓄させる年金制度、
義務教育の必要性も同じ理由となる。
保険というのは、加入者が多くなるほど大数の法則が生かせる。
規模の経済みたいなもので、母集団の期待値(母平均)と、標本平均が、完全に一致する。
ただしこの理由だけでは、別に民間の保険がダメで、社会保険でなければならない理由にはならないが、
他に根拠として、民間の保険だと逆選択が発生すること。全員が強制加入だと逆選択は起きない。
ただし、逆選択の方はそれで解消できても、モラルハザードの問題は、民間の保険と同様に社会保険でも起きる。
民間の保険でもよく用いられているモラルハザードを防ぐ制度として、完全保険にしないこと。
完全保険とは、事故・病気・火災などの損害が、起きても・起きなくても、所得水準が同じになるような保険。
損失が完全にカバーされているという意味だろう。
ちなみに、公正な保険というのは、保険会社の利潤が(参入により)0となるような保険。
完全保険にしないってことは、何か損害が発生しても、被保険者に一定額を必ず負担させるということ。
医療保険の自己負担制度とか。完全に保険で無料だと、やはり医療サービスの消費は過大となる。
1000円でも自己負担があれば、過剰消費を減らせるだろう。
他にも免責条項を設定して、被保険者がそれに違反するような危険な行動を取れば保険金が減少したり、
逆に一定期間無事故であれば保険料を下げるなどの制度もある。
○ 12章3節、年金。
年金保険とは、所得が得られなくなる老後において、予想よりも長生きしてしまった人と、
早く死んでしまった人の間での再分配を通じた、リスクをシェアする機能。
ただし、民間保険には逆選択の問題があり、老後のための貯蓄(自己保険)には、
政府の救済を期待した動学的不整合性の問題がある。
強制加入の社会保険(公的年金保険)は、両方の問題を解決できるが、モラルハザードの問題もある。
モラルハザードの問題はちょっと置いておいて、本節では世代重複モデル(OLGモデル)で、
年金制度の比較を行ってみよう。代表的個人モデルと違って、家計は一定期間後に死ぬモデル。
・登場する経済主体は、死なない政府と企業。一方で、t期に生まれてt+1期に死ぬ家計(2期間OLG)。
・政府は公的年金の運営のみ。それ以外の政府活動は行わない。
・家計は若年世代(t期)に賃金所得(wt)を得て、老年世代(t+1期)では自分の貯蓄と年金だけで生活。
・払うのが保険料、もらうのが保険金(以下、給付金とする)。加入者を被保険者、運営する側を保険者。
・t期の所得にかかる保険料率=τt
・t+1期の若年世代の所得wt+1に対して、t+1期の老年世代が受け取る給付金の比率=所得代替率(st+1)。
このように記号を定義すれば、t+1期の給付金は逆に次のように表現できる。
t+1期の給付金/wt+1=st+1 → t+1期の給付金=st+1・wt+1
・t期に生まれた世代の、t期における消費=c1t、t+1期における消費=c2t
・t期の若年世代が、次期に持ち越す資産(すなわち自分で行うt期の貯蓄)=at+1(t+1という表記に注意)。
運用先は企業への投資と、公債の購入。
c1t=(1-τt)wt-at+1 ・・・1
c2t=(1+rt+1)at+1+st+1・wt+1 ・・・2
教科書とは式番号を変えるので注意。式番号を振ってなかったり、番号が大きくて重たいので。
1式のat+1を2式に代入すると、2期間モデルでよく見る家計の予算制約式、
c2t st+1・wt+1
c1t + ────── = wt - (τt・wt - ───────) ・・・3
1+rt+1 1+rt+1
3式右辺の第2項(括弧全体)は、政府に対する家計のネットの支払い(純支払い)の割引現在価値。
つまり、支払いと受け取りの差額の割引現在価値で、それをTと表記すると、t期のTは、
st+1・wt+1
Tt=τt・wt-─────── ・・・4
1+rt+1
企業がt+1期に利用できる資本ストックは、家計のat+1だけではなく、
政府が資産を持って運用する資産もある(at+1はすでに税引き後なので)。
政府は公的年金以外に活動していないので、運用するなら企業しかないからである。
その政府の持ち越す資産がマイナスなら、借金していることを意味し、公債が発行される。
企業の投資から得られる利子率より、公債の利子率が低いと、家計に公債を買ってもらえない一方、
わざわざ高くする必要もないので、公債の利子率と企業への投資で得られる利子率は、rt+1で等しい。
t期に発行された公債は、もし公債の中立命題(リカード=バローの等価定理)が成り立つのなら、
t期の若年世代は、公債償還=増税に備えて、その分貯蓄する。
OLGモデルなので、t+1期では老年世代となっていて働いていないので、所得税を払う心配はなく、
t+1期には死ぬのだが、増税のタイミングがt+1期以降であったとしても、
利他的遺産動機があれば、中立命題は成り立つ(本書のP353を参照)。
しかしここでは、中立命題は成り立たないと仮定して、t期に発行された公債は、
t期の若年世代の増税につながらなければ、家計はat+1(すなわち貯蓄)を増やさないとする。
政府がt期に公債を発行して得た歳入は、t期の公的年金保険の給付に使われるのならば、
t期の老年世代の消費に使われるだけとなる(後述の賦課方式のケース)。
たぶん本書では、わざわざ借金してまで政府が企業へ投資を行うことはないという想定なのだろうと思うが、
以上の設定により、経済全体で企業が利用できる資本ストックは、at+1から公債を差し引いたものとなる。
すなわち、公債の発行(=即給付の一方で貯蓄は増えない)によってクラウディング・アウトが起きることになる。
もし中立命題が成り立っていれば、たとえ完全雇用が成立していても、
公債の発行+減税(や給付)は、同額の貯蓄が発生するので、クラウディングアウトは起きない。
(もしくは、後述の積み立て方式の場合には、クラウディングアウトは起きない。)
あるいは不完全雇用+金融緩和がセットならば、公債発行+公共投資でもクラウディングアウトは起きない。
例えば、10兆円の公共投資が行われれば、乗数過程において必ず10兆円の貯蓄も発生する。
・中立命題○ならば、限界消費性向c=0。公共投資で国民が受け取った所得10兆円は、そのまま全額貯蓄される。
ただし、均衡予算乗数=1なので、GDPは増える。
・中立命題×でc>0、例えば0.6としよう。10兆円の所得が発生すれば、4兆円の貯蓄+6兆円の消費、
さらに6兆円の所得発生から、2.4兆円の貯蓄+3.6兆円の消費、
さらに3.6兆円の所得発生から・・・・と計算していけば、
乗数過程で発生している貯蓄を合計すると、ちゃんと10兆円になる。
Y=C+Gで、C=cYを代入すると、Y=G/(1-c)。
公債発行で賄うので租税Tを無視すると、S=Y-C、S=Y-cY=(1-c)Y=G。
・ 財政方式と給付方式
財政方式:2種類あって、賦課方式と積立方式。
給付方式:2種類あって、確定給付と確定拠出(後者は、被保険者が運用リスクを負う。)
本書ではリスクの問題は扱わないので、給付方式の違いは区別しない。
財政方式で問題となるのが、政府の予算制約式。
・ 賦課方式では、積立金も公債発行もない。t期の人口をNtとすると、
賦課方式での予算式:Nt・st+1・wt+1=Nt+1・τt+1・wt+1 ・・・ 5A
t期に生まれた世代は、右辺のt+1期の若年世代が支払った保険料を、給付してもらう。
Ntは、Nt+1と、等しいとは限らないので、wt+1に対する比率を表すst+1は、τt+1と等しいとは限らない。
・ 積立方式では、政府に積立金があり、それを政府が運用しているので、
積立方式での予算式:Nt・st+1・wt+1=Nt・τt・wt・(1+rt+1) ・・・6A
t期に生まれた世代は、右辺のt期で支払った自分の保険料を、rt+1で運用してもらって給付を受け取る。
支払いも受け取りも、どちらも自分なので、両辺ともNtである。t+1期の世代は出てこない。
ただし、左辺には相変わらず、wt+1が出てくる。
st+1の定義が、t期の老年世代が受け取る給付金の、t+1期の若年世代の賃金wt+1に対する比率だからだ。
・ τt=τと一定にした上で、両方式の違いを見てみる。予算式5A式を踏まえた上で、まずは賦課方式から。
Nt+1・τ
Nt・st+1・wt+1=Nt+1・τt+1・wt+1 → st+1=────── ・・・5B
Nt
t期の若年世代のネットの支払いである4式に、5B式を代入すると、
st+1・wt+1 Nt+1 wt+1 τwt
Tt=τt・wt-───────=(1+rt+1 - ───・────)・───── ・・・7A
1+rt+1 Nt wt 1+rt+1
7A式の右辺の括弧の中が、マイナスだった場合、右辺全体でマイナスとなるから、左辺もマイナスとなる。
Ttは割引現在価値で見たネットの支払なので、それがマイナスということは、受け取り超過を意味する。
Nt+1 wt+1
───・──── > 1+rt+1 ・・・8A
Nt wt
ここで次のような記号を準備する。
Nt+1-Nt Nt+1 Nt+1
人口成長率:──────=───-1=nt+1 → 1+nt+1=─── ・・・9A
Nt Nt Nt
wt+1
賃金成長率:1+γt+1=─── ・・・9B
wt
8A式に、9A式と9B式を代入すると、
(1+nt+1)(1+γt+1)=1+nt+1+γt+1+nt+1・γt+1 > 1+rt+1 ・・・8B
nt+1とγt+1はゼロに近い数字なので、その積の項(nt+1・γt+1)は無視できるとすると、
nt+1+γt+1 > rt+1 → 人口成長率+賃金成長率 > 利子率 ・・・8C
8A式が成立していれば、賦課方式のおかげで払った以上にもらえる。
その原資は次の世代の所得からなので、世代間再分配が行われていると言える。
・ τt=τと一定にした上で、予算式6A式を踏まえた、積立方式について。
st+1・wt+1
Nt・st+1・wt+1=Nt・τt・wt・(1+rt+1) → ───────=τt・wt ・・・6B
1+rt+1
t期の若年世代のネットの支払いである4式に、6B式を代入すると、
st+1・wt+1
Tt=τt・wt-───────=τt・wt-τt・wt=0 ・・・7B
1+rt+1
(P367の同式では、中央の辺の2項目の分子は、st+1だけになっているが、誤植だと思う。)
人口成長率も賃金成長率も関係ないので、世代間再分配は生じない。
家計は同質で、かつ、リスクの問題は捨象しており、政府の運用も同じ市場利子率なので、
積立方式は家計の貯蓄と完全に代替的である。
というのも、まず年金制度がない場合の予算制約式を考えてみると、1式~3式を見ればわかるように、
保険料率のτtや、給付金のst+1・wt+1がない。
一方、積立方式の7B式より、3式の2項目が無くなるので、
積立方式の下での家計の予算制約は、年金制度が無いときと完全に同じになるからだ。
積立方式であれ賦課方式であれ、年金制度が存在している時点で、t+1期で給付がもらえることは確かで、
どちらの方式だろうと、家計のt期の予算制約より、at+1は必ず次のようになる。
c1t=(1-τt)wt-at+1 → at+1=wt-τt・wt-c1t ・・・1
従って、τt・wtの分だけ必ずat+1が減少することは間違いない。
賦課方式の場合に問題なのは、Tt≠0なので、所得効果も追加的に生じて、c1tが変化し、at+1もさらに変化する。
資本ストックの量が変化すれば、wtも変化するので、その経路の効果も発生するだろう。
積立方式の場合、Tt=0なので、その効果は生じない。
ただし、P367では、両方式でat+1が減ることをもって、一種のクラウディングアウトと呼べると言っているが、
企業が利用できる資本ストックが減少するかどうかという意味では、賦課方式の場合は上記のようにありうる。
賦課方式の場合、確かに公債は発行しない。しかし、徴収した保険料の運用もしない(資産を持たない)。
t期の若年世代が支払ったτt・wtは、政府に積み立てられて運用(企業向け)されるのではなく、
t期の老年世代にそのまま給付され、同じt期に即座に消費される。
一方、t期の若年世代は、t+1期に給付がもらえることをあてにして、at+1は減らすからだ。
しかし、P368でも書かれているように、積立方式の場合は、企業への投資額=資本ストックは減少しないので、
その意味でのクラウディングアウトは起きない。
年金が貯蓄を完全代替するということは、民間貯蓄が政府貯蓄という名前になるだけで、
貯蓄そのものは全体で減ってない(運用先も一緒)ので、
公的年金制度(積立方式)がある時とない時とで、企業が利用できる資本ストックの量は不変だからだ。
・ P368~P372、人口動態。
積立方式と比べて賦課方式の場合、8C式によって人口成長率と賃金成長率の影響を受ける。
人口動態の影響について考えるために、賃金成長率は一定と考えよう。
ある変数の影響を調べるときには、他の変数は一定とするのが経済学(だけじゃないが)的手法である。
nt+1が低下すれば、t+1期の老年世代にとって、年金の原資となるt+1期の若年世代の所得合計は少なくなる。
子育てに伴う色々な費用を払って来なかったと言えばそれまでだが、年金だけを見れば損をする。そこで、
t+1期の給付金/wt+1=st+1
であったことを思い出そう。なぜこのような記号をわざわざ定義したかというと、
人口成長率が変化しても、st+1=sで一定ならば、t+1期の老年世代が損をするとは限らないからだ。
(一方で、仮定により賃金成長率は不変だし。)
賦課方式の予算式5A式と、人口成長率の9A式を再掲して、ネットの支払い4式について改めて見てみると、
Nt・st+1・wt+1=Nt+1・τt+1・wt+1 ・・・ 5A
Nt+1
1+nt+1=─── ・・・9A
Nt
st=st+1=st+2=・・・=sとすれば、5A式は、1+nt+1=s/τt+1となるので、
st+2・wt+2 wt+1 wt+2
Tt+1=τt+1・wt+1 - ───────=(───── - ─────)・s ・・・7C
1+rt+2 1+nt+1 1+rt+2
人口成長率の1+nt+1が小さくなれば、t+1期における若年世代のネットの支払いは大きくなる。
これまでの分析では、τt=τで一定にしていたので、
賦課方式の下で人口成長率が変化すると、5A式で言えば、その影響はst+1に現れていた。
今度は、st+1=sで一定と考えるので、5A式で言えば、左辺全体を一定としたまま
Nt+1の減少をτt+1の上昇で相殺していることになる。
次に、積立方式の場合について。人口成長率がどうなろうと、ネットの支払いは常にゼロなので、
各世代の負担は変化しない。
・ わからないことを、正直に告白。
P369の一番下の行~P372の、賦課方式から積立方式への移行と世代間負担の話が、
個人的にまったく分からない。
t期に移行するとして、t-1期の若年世代が払った保険料は、t-1期の老年世代にすでに支給されている。
t期の若年世代は、t-1期の若年世代(t期の老年世代)に、保険金を支払いつつ、
自身がt+1期で保険金をもらうために、積立金も払わなければならない。
移行期であるt期に負担が集中し、2重の負担と言われる。
t期以降のすべての世代に公平に負担してもらうために、
永久公債を発行しつつ、(永久公債なのに)償還していくとする。
人口N、賃金率w、利子率rを一定とし、償還財源も労働所得税として、すべての世代に公平にτとする。
(なんか同じ記号だけど、積立制度の年金保険料のτとは別に、追加で払っていることになると思う。)
t期以降が負担した税の、割引現在価値の合計は、無限等比級数の公式より、
Nτw Nτw 1+r
Nτw+────+──────+・・・=────Nτw
1+r (1+r)^2 r
ここまでは分かる。理解できないのはここからで、なぜかP370の下から5行目で、
移行期であるt期の老年世代に支払う保険金を、Nsと言っている。もう1度書くが、
t+1期の給付金/wt+1=st+1 なので、Nswじゃないのかな?
そこで、次のサポートウェブの正誤表を見てみると、
http://yuhikaku-nibu.txt-nifty.com/blog/2010/10/post-d373.html
[誤]これが移行時点での引退世代への年金給付Nsに等しいから
[正]sを1人当たり給付額と読み替えると,これが移行時点での引退世代への年金給付Nsに等しいから
とのことらしいが、それでも分からないw
結果、下から4行目で、
r
τw=────s
1+r
と書いてあるけど、忘れている設定や記号があるのかと何度も読み返したが、分からない。
左辺はτだけじゃないのかな?
さらに、P372の1行目で、12-13式(本ノートでは、7A式)に、
Nt+1=Nt、wt+1=wt、rt+1=rt、を代入するというのは分かる。
ところが、最後にτwt=sを代入して、
r
T=────s
1+r
となるから、移行後の世代の負担は、賦課方式を存続させたときと比べて変化しない。
と言っている。???である。
同じ記号τを使っているけど、賦課方式のままなら、本来なら追加で負担は発生しないはずなので、
変化しないというのはありえないと思うんだけど、自分が間違っているとしたらどこなのかも分からない。
そもそも、τwt=sを代入というのが突然出てくるのだが、なぜなのか・どういう意味なのかまったく分からない。
何度も読み返してチャレンジしているのだが、未だに分からない。
・ 賦課方式から積立方式への移行と、「課税標準化理論」
t期に移行する場合、t-1期の若年世代はすでに保険料を支払っている。
しかしそれはt-1期の老年世代に給付されてしまっている。
t期の若年世代は、積立方式なのでt+1期で老年世代になった時のために、
t期において積立金のための保険料を支払いつつ、
t-1期生まれでt期に老年世代になっている人の保険金給付も支払わなければならない。
「二重の負担」と言われ、t期の若年世代だけが移行の負担を全部引き受けることになる。
それでは世代間で不公平だということで、発生した負担をt期以降の全世代に、
平等に負担してもらおうという発想が出てくる。
それが、「課税の標準化」と言われる概念で、本ノートではちょっと前後するが、
本書ではちゃんと12章の2節で先に説明される。
上記の年金制度移行の負担に限らず、t期の公共財の供給費用の負担について、
その公共財の便益がt期以降の世代にも及ぶのなら、
最初の資金調達は国債発行で調達して、その国債の償還は各世代でまんべんなくという発想だ。
・ 12章4節、世代間の公平性。短いが素晴らしい文章だと思う。
それでも全部書き写すのはしんどいので、要点をまとめると、
・世代間の所得移転により、支払っている世代を損、受け取っている世代を得、という単純化は正しいだろうか?
・基準は所得移転だけではない。技術進歩、民間の資本ストック、社会的インフラ、etc。
・技術進歩、資本蓄積、経済成長がある中では、後の世代から前の世代への所得再分配は否定しえないだろう。
(例えば、負担能力の高い先進国が後進国へと再分配することは、良いことだろう。)
・公的年金や公債発行は、どの世代に属するのかわからないというリスクをシェアする機能がある。
・教育投資や贈与・相続は、上記とは逆に、前の世代から後の世代への所得移転とも言える。
・つまり世代間の所得移転は、それだけで世代間の公平性を損なうものとは限らないということ。
・だからと言って、過度な所得移転は、それはそれで不公平である。
・特に経済成長率が低下すると、後から前への所得移転は是認されにくくなるだろう。
・経済成長が低下し始める最初の勤労世代は、賦課方式から積立方式への移行と同様に、負担が集中する。
・公平観は社会の価値判断に依存するとはいえ、負担が集中することは制度そのものへの否定につながりやすい。
・制度の時間的視野に比べて、家計のそれは短い。従って制度設計時点で参加していない可能性もある。
・価値判断の問題とはいえ、メリット・デメリットを含めた情報公開と、十分な理解と検討がまずは必要。
経済学ノートのトップページに戻る
このような合成財をニュメレールといい、その価格は1に基準化することが多い。
そして公共経済学の分野では、準線形効用関数(分析の対象となる財の、需要の所得効果が0)という仮定が、
かなり頻繁に用いられる。結構クリティカルな割には、ちゃんと説明している教科書が少ない。
もし準線形選好を仮定しない場合、
コースの定理:
権利をどちらに配分しても、資源配分は同じ(結果は同じ)・・・ではなくなる。
交渉の結果は相変わらずパレート効率的ではあるが、権利の配分次第でパレート効率的水準(資源配分)は
不変でなくなる。
公共財:
サミュエルソン条件は相変わらずパレート効率的ではあるが、公共財の最適供給量が一意に決まらない。
ピボタル・メカニズム(クラーク=グローブス・メカニズム):
そもそも成立しない。
個人的には大問題だと思うんだが、経済学者でこのことをちゃんと強調して語っている人っているのだろうか?
所得を人質にされて、欲しくも無い公共財に賛成票を投じざるを得ない人達のドキュメントとか見てるとね・・・。
● 目次
・「林正義 吉田浩 財政学をつかむ 有斐閣 2008/06」の6章、医療・介護と育児・教育
・「常木淳 公共経済学 新世社 第2版 2002/03」
・「ハル・R・ヴァリアン 入門ミクロ経済学 勁草書房 第9版 2015/08」
・「林正義 小川光 別所俊一郎 公共経済学 有斐閣 2010/12」
・「柴田弘文 柴田愛子 公共経済学 東洋経済新報社 1988/12」
・「板谷淳一 佐野博之 コア・テキスト公共経済学 新世社 2013/01」
・コースの定理
・林公共の10章と12章
● 「林正義 吉田浩 財政学をつかむ 有斐閣 2008/06」の6章、医療・介護と育児・教育
教科書内では、unitという単位で区分されていて、unit23が医療・介護、
unit24が育児・教育となっている。
まず医療保険の公的供給の根拠について。
病気のほとんどに言えることだが、早期発見・早期治療。その方がかえって費用負担も小さいことを踏まえた上で、
1:価値財。
2:感染や公衆衛生などの外部性。
3:所得再分配政策として、現金給付ではなく現物給付。
医療そのものの供給に関する公的関与の根拠。
1:医療従事者に求められる一定の知識・技術の水準は非常に高いので、人的資本への投資に掛かる費用も大きい。
教育への公的関与にも言えることだが、後で賃金所得によって回収できるとしても、
資本市場が不完全だと過少供給になりやすい。
2:入院施設や医療機器などの施設・設備は初期費用が高い。固定費用が小さくなく、費用逓減産業。
3:医療だけではなく、サービス産業全般に言えることだが、貯蔵・運搬が難しいので、地域的偏在が起きる。
子供に対する需要を経済学的に考察。
1:子供がいるということ自体に効用を感じるという意味で、消費財としての子供需要。
消費財(ニュメレール)=c、子供の数=n、1人当たり子育ての費用=pとすると、
効用関数:U(c,n) 、 予算制約:y=c+pn
食事や衣類、保育園や幼稚園、塾や習い事といった教育費が高くなれば、子供に対する需要は低下する。
2:子育てにかかる時間という機会費用。
時間全体=H、1人当たり子育て時間=h*、労働供給に割ける時間=h、賃金率=wとすると、
時間制約:H=h*+h
予算制約:y=wh=w(H-h*)=c+pn → wH=c+pn-w・h*
賃金率wが上昇すると、子育てに使う時間の機会費用が大きくなる。
3:老後の生活を賄うための、投資財としての子供需要。
医療・介護、年金などの保険やサービス(介護サービス事業など)は、
公的供給だけではなく、民間の供給も増えているので、市場サービスの代替としての子供需要は減りつつある。
4:労働力としての子供。
産業構造が農業中心だった時代では、なるべく多人数で共同で行うのが効率的。
実際に農繁期などは学校を休みとして働き手として期待された時期も存在した。
農業自体が機械化されたり、産業構造全体でも農業部門が縮小してきたので、子供需要も減少。
教育に対する公的関与の根拠。
まず数字的には、日本の教育に対する公的な支出水準は、
初等・中等教育まではOECD各国の平均レベルだが、高等教育になるとその平均を大幅に下回ることで有名。
1:一番有名なのが人的資本論。
これに対して、教育には人的資本を増やす効果は無いという意見も存在する。
高学歴な者ほど高賃金というのは、ゲーム理論や情報の経済学的に言えば、
シグナリング(大卒などの資格を取る)や、企業によるスクリーニング(入社試験や面接)の結果であって、
元々高い能力の人が、学歴によってその能力を顕在化させているに過ぎないとのこと。
義務教育までの基礎教育は生産性を上昇させるが、その影響を除いた上で、
高等教育については、その部分だけで純粋に個人の生産性を向上させることは確認されてない
という研究結果も報告されている。
2:外部性。
人的資本の蓄積による成果が、個人の収入に反映されるならば、教育にかかる費用は、
個人の将来においてすべて回収可能ということになる。
しかし、仮にそうであっても、外部性がある場合には過少となる。
一緒に仕事をする場合、相手の能力が高いほど、自分の成果も高まる。
逆も言える以上、お互いの能力が高いほど、生産性は飛躍的に向上する。
3:機会の均等化という公平性と、不完全な資本市場。
単に資本市場が不完全なだけではなく、もう1点重要なのが、教育支出の意思決定は未成年時になされること。
その際、親の資金力(収入)が教育の需要量を決定してしまう。
(親の収入が低い家庭では、親に迷惑をかけたくないという孝行心から、進学を諦める子供もいる。)
ただし、教育サービスの供給者に公的な支出が望ましいとは限らない。
不完全な資本市場が問題なら、教育費をただ引き下げるのではなく(それだと金持ちの子も恩恵を受ける)、
資金を必要とする人への奨学金制度の充実という方向もある。
教育の供給者ではなく需要者に支援という意味では、教育バウチャーなどもある。
教育バウチャーに関する実証研究をまとめた論文としては、次の赤林英夫の論文が面白かった。
http://web.econ.keio.ac.jp/staff/hakab/whatisvoucher20061116.pdf
人気校の周辺の土地は金持ちが買って地価が高くなり、結局貧乏人は人気校に行けないなどの懸念もあるみたいだが、
低所得者だけ補助金を出す方法もあるようだ。
学力向上に有意・有意でないのどちらの実証もあって結論が出ていないようだ。
それよりも本論文で解説される視点は目からウロコ。私立学校というのは受験を通して生徒を選択できる。
しかし教育バウチャーによって私立を含めて生徒側が学校を選択できるようになれば、
私立学校は生徒を選択できなくなるという意味でトレードオフであり、
結果、教育バウチャーは私立の公立化を意味する。
● 「常木淳 公共経済学 新世社 第2版 2002/03」
7章2節、効用関数を同一と見なせるかどうかにおけるラーナーの議論が重要で、
柴田公共ではP224~P227で説明される。
林公共のP278~P280にも、同質の効用関数に関する議論があり、
特にP280の「第2」は、ラーナーの議論に相当する。
ベンサム型とロールズ型の説明については、板谷公共の3章5節~8節(p79~p97)も参照。
○ 7章1節、社会的公平とは。社会的厚生関数と原初状態と無知のヴェール。
社会的厚生関数と社会的無差別曲線の違いは、前者が多数の人々の効用関数で構成される関数なのに対し、
後者はそれを2人に絞ることで2次元の無差別曲線図として図示したもの。
縦軸および横軸は、2人の効用水準を取る。
一方、国際貿易論では生産可能性曲線(PPF)と、1国全体の無差別曲線として社会的無差別曲線が登場するが、
横軸にX財、縦軸にY財をとった2次元のグラフで、社会的厚生関数とは関係ない。
社会的厚生関数は財平面ではなく、個人間の効用平面に描かれ、
個人間の効用水準の「配分」の望ましさを考えるのが目的。
功利主義的社会的厚生関数(ベンサム=ピグー型社会的厚生関数)
効用関数は各個人において同一で、かつ、測定・比較・加算が可能で(効用関数を足し算するので基数的)、
社会全体の効用の和を最大化(最大多数の最大幸福)
W=Σui 1≦i≦n ・・・B
このような社会的厚生関数に理論的な根拠を与える方法として、ハーサニーによる原初的無知のヴェールがある。
各人の社会的位置に関する代替的な選択肢が存在するときに(色々な立場・状態の人がいるときに)、
それらの各位置で当人が得る効用の評価が各人共通であるという仮定を立て、
(つまり同一の効用関数を仮定。その理論的根拠については後述。)
かつ、社会の構成員は自分がどのような社会的位置にあるかまったく不確実であるために
それらすべての可能性を「等確率」と仮定。
A、B、C、Dの4人世界の場合、いったん原初状態に立ち返り(その時に無知のヴェールを通り抜ける)、
そこから各人とも4人の中のどの状態・立場の人間として生まれるかは、
無知のヴェールによって1/4の確率ずつと考える。
すると各人(個人個人)がこのような条件下で獲得する効用の期待値は、
すべての可能な社会的位置で、各人が獲得する効用を(つまり全員の効用を)
足し合わせたもの(に等確率を乗じたもの)になる。
しかも各状態での効用評価は各人共通と仮定しているので、
(各人が原初状態で計算した)効用の期待値は各人共通となる。
かくしてB式に基づく社会的決定を行うということは、原初状態と無知のヴェールの下で、
各人が不確実性下での「危険中立的」な最適化行動に基づく、合意可能な価値判断となる。
つまり期待効用理論において、期待値だけを考慮したリスク中立型の効用関数(線形)となる。
横軸にu1、縦軸にu2を取ると、功利主義の下では、u1+u2の合計Wが同一の値ならば、
各状態は等確率なので結局は期待値も同一となる。
同一の社会的厚生をもたらす効用配分の集合である社会的無差別曲線は、右下がり(45度)の直線となる。
u2=-u1+W ・・・B’
ロールズ型社会的厚生関数はマキシミン原理に従う。原初状態と無知のヴェールの仮定の下での最適化行動として、
一番不幸な人の効用を、最も改善させるのが合理的であると考える。従って社会的無差別曲線はL字型となる。
効用が最低の人だけを考慮するので、効用関数が比較可能であればよく、基数的じゃなく序数的であって構わない。
序数的なら「同一の(重要)」増加関数による単調変換で、社会的順序(その中で最低の人)は不変だから。
ハーサニとロールズがともに依拠した原初状態と無知のヴェールの仮定は、次のように理解できる。
社会的に公平な判断を各自が行うための自然な発想として、
メンバー全員が自分の立場・状態をひとまず括弧に入れてみることだ。
自分の能力や財産などをいったん無視し、各人が他人の様々な境遇を、自分にも降りかかる可能性のあった問題として
真剣に考えることが、公平について考えるときの思考実験として「公正」と言える。
同一の効用関数、原初状態と無知のヴェールの仮定によって、ベンサム型も、ロールズ型も、
社会的無差別曲線は原点から右上がりの45度線を軸に左右対称となる。
ベンサム型だと、完全に効用は互換可能である。
裕福な人の効用が1単位増えれば、貧乏な人の効用が1単位減っても社会的厚生関数上、無差別となる。
社会全体の効用の総和しか論じないので、極端な話、誰か1人が富を独占している状態も許容される。
ロールズ型だと、トレードオフは不可能である。
ロールズ型の問題点としては、効用が最低の人だけを考慮し、それ以外の人をまったく考慮しないこと。
例えば家計1から家計3まで3人いたとして、
所得分配A:(300,500,500)
所得分配B:(290,1000,1000)
マキシミンの原理に従うロールズ型だと、所得分配Aの方が厚生が高くなる。
各家計がリスク回避的だとしても、まったく一切リスクを取らないというのも非現実的である。
要求するリスクプレミアムを超えるならば、不確実な状態を選択する場合だってあるだろう。
ベンサム型とロールズ型の間を取るような社会的厚生関数の例として、ナッシュ型の社会的厚生関数があり、
ナッシュ型の社会的無差別曲線は、
W=u1・u2 → u2=W/u1 ・・・C
効用の積で表現されるので、u1-u2平面(効用平面)でのグラフは、反比例(非線形)となる。

原点から右上がりの45度線との交点付近では、効用は交換が可能だが、
45度線から離れるにつれて、より裕福な人の効用を増やすために、
減らさなければならない貧しい人の効用は小さくなるとする(限界代替率が逓減)。
不平等度が著しく高い場合には、ほとんどロールズ型に近くなり、交換不可能となる。
このような社会的厚生関数は、より貧しい状態の効用を、裕福な状態の効用よりも高く評価するという意味において、
危険回避的な最適化行動をしていると考えられる。
ちなみに社会的無差別曲線を図示する時に描かれるのは、
純粋交換経済で考える場合には効用可能性曲線(UPC:utilty possibility curve)、
生産経済で考える場合には、効用可能性フロンティア(UPF:utilty possibility frontier)。
生産に関しては生産可能性曲線=生産可能性フロンティア(PPF)なので注意。
生産経済を考える場合は、PPF上を移動するに従って、
その内部に形成されるエッジワースのボックスダイアグラムが、いくつもできる。
従って効用可能性曲線もその度にできるので、効用可能性曲線群の包絡線が、効用可能性フロンティア。
○ 7.2節、ラーナーの議論。効用関数の同一性について、さらに原初状態と無知のヴェールの仮定を用いてみる。

P188の図7.2より、もし限界効用が逓減するなら、限界効用が均等化する(所得)分配Aが、
u1+u2=効用和(グラフの下側の面積OaCbO’)を最大にする。
(限界効用が逓減することを前提にしているので、効用関数はリスク回避型である。
ちなみに「配分」と「分配」の使い分けは、「資源は配分」、「所得は分配」。)
ラーナーによると、効用関数の同一性に関しても、原初状態と無知のヴェールによって根拠を与えられる。
効用享受能力もまた、原初状態における社会的位置の可能な選択肢、構成要素の1つと考えられるからだ。
図7.2では、効用関数が違うaとbの限界効用曲線(どちらも所得に対して減少関数)が描かれている。
左の原点Oからaの所得、右の原点O’からbの所得を取り、縦軸に限界効用を取る。
aの方が効用享受能力が高い場合、aの限界効用曲線の方が位置が高い。
すると、aとbの限界効用曲線の交点は、真ん中より右側に位置する。
限界効用が均等化している交点をC、そのときの所得をA点とし、両者の所得合計のちょうど半分の所をB点としよう。
そこでA点から所得の再分配によりB点にしたとすると、三角形CDEの厚生損失が発生する。
しかし効用享受能力も、原初状態と無知のヴェールによって、お互い真逆の効用関数だった可能性を考慮してみよう。
効用関数の位置関係(左からの限界効用曲線の方が位置が高い)はそのままに、aがbに、bがaになりつつ、
元々の所得分配を考察するには、B点を軸にA点と対称な点A’を、出発点に考えなければいけない。
A’点から出発して、所得の再分配によりB点にしたとすると、発生する厚生の「増加」は、台形GFDEとなる。
これは先ほどの厚生損失の三角形CDEよりも大きい。
たとえ効用享受能力に個人差があっても、2種類の厚生変化が「等確率」で生じる原初状態と無知のヴェールの下では、
台形>三角形であることから、所得再分配によるB点の実現は、期待効用和を純増させる。
結局、このような思考実験により、効用関数の同一性を認めることが可能となる。
● 「ハル・R・ヴァリアン 入門ミクロ経済学 勁草書房 第9版 2015/08」
○ 準線形効用関数(準線形選好)と、ニュメレール(合成財あるいは貨幣所得)
準線形効用関数(準線形選好)については、 ミクロ経済学ノートを参照。
次章の林公共や、最後の方にあるコースの定理を理解する上で、必須の前提条件なので、
先にミクロ経済学ノートを読んでおこう。
一方、分析したい対象の財以外の、全ての財を合成した財=貨幣所得と捉え、
そのような合成財をニュメレールといい、その価格は1に基準化することが多い。
○ 37章、公共財。
2人経済を考え、
・各人の私的財消費量:x1、x2
・各人の富の初期保有量:w1、w2
・各人の公共財に対する費用負担:g1、g2
・各人の公共財に対する留保価格:r1、r2
それぞれの予算制約式は、
x1+g1=w1
x2+g2=w2
公共財の購入に掛かる費用をcとすると、次の制約も満たさなければならない。
g1+g2>c
個人1の効用関数を次のように表記する。
u1(x1,G)
G=公共財で、個人2も同時に等量消費可能。Gは0と1の値を取り、0なら公共財が無い、1なら有る。
留保価格=支払意思額
消費者が買ってもいいと考える上限価格で、購入するか・しないか、が無差別となる価格なので、
u1(w1-r1,1)=u1(w1,0) ・・・1
「もし公共財への支出がパレート改善可能ならば?」
u1(w1,0)<u1(x1,1)
u2(w2,0)<u2(x2,1)
左辺に留保価格の定義1式、右辺に予算制約式を用いると、
u1(w1-r1,1)=u1(w1,0)<u1(x1,1)=u1(w1-g1,1)
u2(w2-r2,1)=u2(w2,0)<u2(x2,1)=u2(w2-g2,1)
効用関数は、xの増加関数なので、不等号をそのまま用いることができて、
w1-r1<w1-g1
w2-r2<w2-g2
よって、パレート改善が可能であるためには、次が必要条件となる。
r1>g1
r2>g2
次のパレート改善の十分条件が満たされれば、両者を改善する支払計画が必ず存在することを意味する。
r1+r2>g1+g2=c ・・・2
・ ここまでの注意点
ここまでは効用関数について準線形選好であることは仮定してない。
従って、一般的に留保価格r1、r2は、富の初期保有量に依存するだろう。
ある富の分配では、r1+r2>cであったものが、別の分配に対しては、r1+r2<cとなることもありえる。
極端な例として、富を独占する1人の富豪と、大多数の貧しい人がいる状況で、
富豪がその公共財に対する選好が強く、留保価格が高ければ、自分で費用を全額負担しようとするだろう。
逆に富豪がその公共財に対して無関心ならば、大多数の貧乏人が必要としていても公共財を購入しないことが
パレート効率的になってしまう。
・ いよいよ準線形効用関数
公共財に対する需要が、所得や富から独立と仮定してみよう。準線形効用関数の定義より、
個人1の準線形効用関数:u(x1,G)=x1+v1(G) ・・・3
このように定式化すると、対象となる財はGであり、それ以外の私的財x1はニュメレールとなる。
単純化のために、v1(0)=v2(0)=0としよう。この場合、留保価格の定義である1式より、
u1(w1-r1,1)=w1-r1+v1(1)=w1+0=u1(w1,0)
u2(w2-r2,1)=w2-r2+v2(1)=w2+0=u2(w2,0)
となり、これより、
r1=v1(1) ・・・4
r2=v2(1) ・・・5
公共財に対する需要が、所得や富から独立であることから、公共財に対する留保価格も所得や富から独立となる。
・ 37章4節、P648~、公共財の最適供給(サミュエルソン条件)
MRS1=個人1における、私的財に対する公共財の限界代替率、dx1/dGとすると、
MRS1+MRS2=MRT(限界変形率=生産可能性曲線(PPF)の傾き)
MRT=相対価格(pG/px1)=MCG/MCx1 ・・・6(利潤最大化条件のP=MCより)
・ 37章5節、P651~、準線形選好と公共財
一般的な公共財の最適供給の問題(サミュエルソン条件)に、準線形選好の仮定を導入してみよう。
私的財xに対する効用は線形で、その限界効用は1である。限界代替率=限界効用の比なので、
MRS1=dx1/dG=MUG/MUx1=MUG=∂u1(x1,G)/∂G ・・・7
個人2についても同様で、結局、限界代替率はGのみに依存する。
そしてサミュエルソン条件より、x1やx2とは無関係に、公共財の最適供給量(効率的水準)は一意に決まる。
2人の間で私的財をどんなに再分配しても、2人の無差別曲線の傾きである限界代替率は変化しないので、
公共財の供給量が効率的水準で一定なままなので、私的財と(供給量一定の)公共財のあらゆる資源配分は、
すべてパレート効率的である。
当たり前っちゃ当たり前である。私的財は関係ないのだから。
誤解しがちなのが、別に準線形選好の仮定が無くても、サミュエルソン条件はパレート効率的である。
ただ、その最適供給量が一意に決まるかどうかが、今問題にしている準線形選好の仮定と関係してるだけ。
・ 37章の6節~8節、P652~、フリーライダーと公共財の供給量の決定問題(特に投票)。
私的財は、消費の外部性がないので、市場で個人個人が分権的に意思決定していれば、
全体的にもパレート効率的になる。
神の見えざる手と言われるが、市場(で決まる価格)自体が、民主主義的な投票システムなのである。
しかし、公共財の場合は外部性(市場で直接取引した者以外にも効果が及ぶ)があるので、
フリーライダーの問題も含めると、個人の意思決定だけでは社会的に最適にならない。
公共選択として最も一般的な意思決定メカニズムは、投票である。
しかし推移性を満たさず(循環しちゃう)、社会的決定が不可能となる
(コンドルセの)投票のパラドックスが発生する。
中位投票者定理によると、公共財の量に対する選好が単峰型ならば、社会的決定はできる。
(あくまで、「決定はできる」という程度。)
直感的に言うと、公共財を望む量が小さい方から順番に並べて、
中位より多い支出を望む人(グループA)と、少ない支出を望む人(グループB)は、
中位の定義により半々となるので均衡する。
中位より少ない支出と中位の人が望む支出を比較した場合、グループAは中位の人が望む支出に投票する。
逆に中位より多い支出と 〃 、グループBは 〃 。
しかし、中位投票者定理によって決まる公共財の供給量は、決定はできるが効率的水準であるとは限らない。
半分の人はその中位となる水準より多い支出を望み、半分の人は少ない支出を望むが、
それが定量的にどれくらいなのかは考慮されていない。また、投票結果を操作しようと、
戦略的に行動(自分の真の選好を表明せずに偽って投票)するインセンティブも生じる。
・ ここだけヴァリアンの入ミク(5版)の35章9節、真の選好を表明させるためのメカニズムデザイン。
まず基本的に、公共財の供給が効率的であるためには、個人iの価値(便益)をvi、公共財の費用をcとすると、
Σvi≧c ・・・8
でなければならない。この時点で、準線形選好の仮定が入っている。
2式の十分条件に、準線形選好の仮定を用いて導出した4式と5式を代入すると、8式が導出される。
デザイン1:受益者負担として、表明した価値に比例して費用を割り当てる(リンダール・メカニズム)。
デザイン1の問題点は、フリーライドしようとして、過少申告するインセンティブが生まれる。
そこで個人iの費用負担を、選好表明の前に決定しておくと、
デザイン2:表明した価値viと、分担費用ciが独立。
純価値(純便益)ni=vi-ci ・・・9
後はΣni>0であるかどうかを調べればいい。
しかしデザイン2だと、ni>0の人は、真の価値より過大に申告するインセンティブが生まれる。
過大に申告すればするほど、公共財が供給される可能性が高まるからである。
逆に、ni<0の人は、真の価値より過少に申告するインセンティブが生まれる。
・ ピボタル・メカニズム(クラーク=グローブス・メカニズム)
「奥野正寛 ミクロ経済学 東京大学出版会 2008/04」の7章10節(p340~最後)
奥野ミクロの正誤表、図表集、双対性の詳しい説明が次のサイトにある。
https://sites.google.com/site/okunomicroeconomics/textbook/figures_and_tables
かなりの教科書を読んできたけど、クラーク・メカニズムの説明に関しては、本書が一番簡潔で上手い。
やっぱ図解って素晴らしい。
さて、クラーク=グローブス・メカニズムの成立にも、前提条件として3式の準線形効用関数を仮定する。
そして個人iの費用負担Tiを次のように設計する。
限界変形率=私的財で測った公共財供給の限界費用=c (教科書ではp329に記載)
私的財はニュメレール財と仮定しているので、その価格は1に基準化。
利潤最大化条件のP=MCより、私的財の限界費用も1となる。
その私的財をc単位投入することで、公共財を1単位作れることを意味する(6式を参照)。
cは公共財1単位の(相対)価格でもある。
Ti=cG-Σvj ただしΣの範囲はj≠i、すなわちi以外の全員 ・・・10
もし2人経済だったなら、
T1=cG-v2 ・・・11(教科書では7.11式)
このように設計しておくと、自分の費用負担は、政府に申告する自分の効用(公共財に対する)とは
関係が無くなるため、虚偽報告するインセンティブが無くなり、真の価値を表明するようになる。
その理由を以下の図7.8を用いて説明しよう。

・縦軸は限界効用vi'(G) (vi'(G)>0、vi''(G)<0とする(図では直線になっているけど))
・原点同士の距離=線分O1O2の長さ=c(これ重要1)
まず個人2がv2(G)#を表明しているとしよう。v2(G)#は真の効用関数とは限らない。
このとき、個人1が真の効用関数v1(G)を表明すれば、公共財供給量はG0となるので、重要1より、
総費用cG=四角形O1G0DO2の面積 ・・・12
図7.8に描かれているv2'(G)#は、個人2の限界効用関数であり、準線形選好の仮定の下では、
ミクロ経済学ノートの、 10式より需要曲線でもある。
限界関数と横軸との間の面積が総関数(限界関数を積分すると総関数)なので、
v2(G)#=四角形O2DEFの面積 ・・・13
11式を踏まえると、個人1の費用負担額は、
T1=四角形O1G0EFの面積 ・・・14
となる。一方、個人1の需要曲線はv1'(G)なので、個人1の消費者余剰は三角形FEIとなる。
これに対して、個人1が効用関数をv1(G)#として虚偽申告すると、公共財供給量はG#、
虚偽申告していても真の限界効用関数はv1'(G)なので、12~14式の要領で個人1の消費者余剰を計算すると、
四角形FE'JIになる。
虚偽申告すれば三角形EE'Jの死荷重損失が発生する。Bもまったく同じことが言えるので、
真の効用関数を報告することが、支配戦略均衡になる(相手の戦略に関係ないので)。
均衡点Eでは、v1'(G)+v2'(G)=cが成立しており、6式のサミュエルソン条件も成立している。
ただし、クラーク=グローブス・メカニズムには、1つ重大な問題がある。
14式では個人1の費用負担額T1を導出した。
一方、個人2の費用負担額T2の導出にあたっては、個人1の限界効用関数(需要曲線)v1'(G)を用いるので、
T1=O1G0EF ・・・15
T2=O2DEI ・・・16
総費用cGは12式なので、三角形FEIの赤字が必ず発生してしまう。
● 「林正義 小川光 別所俊一郎 公共経済学 有斐閣 2010/12」
まず最初に、公共経済学の中でも、特に外部性や公共財を理解するにあたっての注意点。
外部性と公共財は、それぞれ別のちゃんとした定義がある。どちらも市場の失敗。
外部性(外部効果)は、取引してる同士「以外」の人、まさしく「市場の外」に効果が及んでしまうこと。
良い効果は外部経済、悪い効果は外部不経済。
公共財は、非競合性(使ってもなくならない)、非排除性(使おうとしている人を排除できない)、
という基準で定義される財。従って発生する問題が、フリーライダー問題。
しかし外部性のある財や公共財を議論するときには、最終的には本質的に同じ構造となる。
外部経済を他者から受け取ることも、外部不経済を他者に与えることも、
どちらも外部効果に対してフリーライドしているのと同じだからである。
その性質のため、個人Aと個人Bにとって等量消費となる。
外部性や公共財の性質から、市場での取引以外の経路で、他者の行動(需要量・供給量)が自分にも影響を与える。
逆に自分も他者に影響を与える。となると、相手の行動を考慮した上で、自分の行動を決定しなければならない。
そのような意思決定を、戦略的意思決定といい、お互いがそのような関係にあることを、戦略的相互依存関係という。
(完全競争市場での意思決定は、自分についてだけであり、消費にしろ生産にしろプライステイカー。)
そこで説明によく出てくるのが非協力ゲーム(囚人のジレンマ)の構造。
相手の戦略を所与(与件)として、こちらの最適反応戦略を求めるという考え方と、
お互いの最適反応戦略同士の均衡点(グラフで言えば交点)が、ナッシュ均衡であるという定義の理解は必須。
民間同士の自発的な行動や市場にまかせておくと、落ち着き先であるナッシュ均衡は、
決してパレート効率的ではない状態となるが、その状態とパレート改善方法(すなわち政府の必要性)が
まさに公共経済学で扱う対象となる。
上記のような問題と、その定式化でおなじみなのが、クールノーモデルである。
市場需要全体が制約条件として入ってきて、それを少数のプレイヤーで奪い合うという構造がクールノーモデル。
市場需要全体に対して、自分の最適な生産量q1を決める際には、相手の生産量q2も自分の問題の中に入ってくる。
その相手の生産量q2を所与(いったん定数)として、自分の最適生産量を求めると、
求まった最適反応関数は、q1とq2の関数となり(q2は変数に戻る)、q1-q2平面にグラフを描ける。
そしてお互いの最適反応関数をq1-q2平面に描いて交点を求めると、それがナッシュ均衡なのである。
(交点を求めるということは、最適反応関数同士を連立させて解く。同時に最適解が成り立つということ。
「戦略的」という単語を見かけたら、このように相手の行動が自分の問題の中に入ってきて、
その相手の行動をいったん所与(定数)として最適化問題を解くと、機械的に覚えておけばいい。
自分のことだけ考えればいいのではなく、相手のことも考えて自分の行動を決定する。)
市場需要を奪い合うように、制約のある資源を奪い合うという意味では共有地の悲劇も同様である。
その数式的な構造は、クールノーモデルと同じであることが、
「中山幹夫 はじめてのゲーム理論 有斐閣 1997/09」の3章3節に書かれている。
中山はじめては、全部読まなくていいが、3章3節だけは図書館などで絶対先に読んでおこう。
ゲーム理論ノートにも引用した。
後、結構出てくるのが、1次同次の生産関数でのオイラーの定理(完全分配定理)。
すなわち、規模に関して収穫一定の場合、利潤は常に0であり、生産物(収入)は生産要素に分配され尽くす。
経済数学ノートの 「21:オイラーの定理」を参照。
さて、いよいよ林の公共経済学に入るが、4章外部性、5章公共財では、
柴田の扇形ダイアグラムを使って説明している。
一般的な消費財の一般均衡の図で有名なエッジワースのボックスダイアグラムに対して、
柴田のダイアグラムは外部性や公共財を図解できて、とても理解しやすくて超便利。
考案したのは次の章で紹介する柴田だが、本書の林公共の方が簡潔に説明していてわかりやすい。
さらに嬉しいことに、次のWEBサイトで、林先生の講義ノートが公開されている。
https://sites.google.com/site/publicfinanceuoftokyo/toppage/public-finance-law
いつ無くなるか分からないので、積極的に図を引用して残しておこうと思う。
林公共の教科書の方の4章と5章と柴田のダイアグラムについては、講義ノートではファイル07になるが、
教科書と同じ図はあるものの、説明文がないのでやはり教科書を読む必要がある。
○ 4章、外部性
教科書のP123より、柴田のダイアグラムが扇形と呼ばれる理由は、
外部性を引き起こす財(5章なら公共財)の、価格(=限界費用)が逓増する場合、
ダイアグラムが扇形になるから。
4章と5章では、価格(=限界費用)は一定と仮定するため、ダイアグラムは直角三角形になる。

Z:外部性のある財(5章の公共財では記号がG)。
個人Aと個人BのZの消費量、ZA=ZB=Z(公共財の場合、GA=GB=G、どちらも等量消費)。
X:ZやG以外のすべての私的財(合成財とかニュメレールといい、価格は1に基準化)。
OBから見ると、上に向かってBの私的財Xの消費量(=XB)。
OAから見ると、下に向かってAの私的財Xの消費量(=XA)。
MAおよびMB(個人の所得)、MA+MB=M(図には無いが、M=総所得)。
ZやGの価格p(=限界費用)は一定で、私的財Xをニュメレールとしていることから、
pはそのまま私的財に対する相対価格にもなる。
1単位のX財を、p単位のZ財に作り変えることができる。従って、OAZmaxの線は経済全体の制約線となる。
右斜め下に伸びる、OAZmaxの線:X=M-pZ
例えばAがZ0を購入し、BはMBを全額X財で消費したとしよう(とはいえ、BもZ0を等量消費せざるを得ない)。
D点から出発して、左にZ財を1単位動かすと、上にp単位移動する。
AのZ財の消費金額は、pZ0円になり、残りのCDの距離がAのX財の消費量XAになる。
すなわち、任意のZ0に対する経済全体のX財の総消費量は、Z0からOAZmax線までの垂直距離
 _
_図4-6の上のa図は、普通の無差別曲線の図。等量消費となるZ(以下、Zバー)からEまでの距離が、
AのX財の消費量となる(E点ではXもZもどちらも最適消費量)。
図4-6の下のb図は、柴田のダイアグラムの図で、Aの無差別曲線の記号は、VAとする。
VAは、下方に位置するほど効用が高い。
E点からZバーまでの距離=斜めのOAZmax線から、真下に向かってF点までの距離(AのX財消費量)で、
図4-5で言えば、CDの距離。
すなわち、HJ線=個人Aの予算制約線(これ大事)
a図とb図は、三角形の面積は同じまま、原点のOAが上下逆転している。

図4-7は、Bにとっての無差別曲線の図で、外部効果を発生させる方をAとしているので、
Bにとって外部経済のときは通常の右下がりだが、外部不経済になると、無差別曲線は右上がりとなる。
Bの無差別曲線の記号はIBとし、柴田のダイアグラムにはそのまま描く。
外部不経済の場合、IBは左上に位置するほど効用が高い。

図4-8は、AとBの無差別曲線を柴田のダイアグラムに描き、両者が接する点の軌跡=契約曲線KK’となる。
外部不経済(タバコ)を例に取り、Aが喫煙者、Bが被害者とする。
Aに喫煙権があると、Bのことを気にせず吸ってしまうので、Aにとってのタバコの最適消費量F点が決まる。
Bは強制的に等量消費せざるを得ないので、F点を通る無差別曲線IBバーになる。
しかしB自身はタバコZを買ってはいないので、MBを全額Xの消費に充てている(Fの高さ=OBHの距離)。
ただし、注意点!!!図4-8と次の図4-9には、誤植がある。次のサポートウェブに、正誤表がある。
http://yuhikaku-nibu.txt-nifty.com/blog/2010/10/post-d373.html
いつかサイトが無くなったときのために引用しておくと、縦軸のOAHの線分について、MB=誤、MA=正。
Bの所得MBは、OBHの距離である。
F点より左下にできるレンズ内部は、両者にとって効用が高くなるので、パレート改善できる。
逆に言えば、外部性が発生している(ピグー税によって内部化されていない)状態では、パレート非効率的となる。
レンズ内部の、さらに契約曲線κκ’の部分を、ミクロ経済学では「コア」という。
コアとなっているZの消費量は、Zバーよりも少ないので、裏を返せば、Zバーは過剰消費である。

図4-9は、外部経済の例で、例えばAが花壇を購入したとしよう。
隣に住んでいるBにとっても嬉しいことなので、IBは右下がりだが、Bは花壇を購入していないので、
MBを全額Xの消費に充てている(Fの高さ=OBHの距離)。
レンズは右下にできているので、Zバーは過少消費となっている。

図4-10で、もしBに綺麗な空気を吸う権利がある場合は、Aは所得を全額、私的財の消費に使うしかないので、
強制的にH点を通る無差別曲線になる。
○ (公共財の)需要の所得効果がゼロの仮定(=準線形効用関数の仮定)
準線形効用関数(準線形選好)については、 ミクロ経済学ノートを参照。
この仮定を置くと、例えば図4-8の契約曲線KK’は、横軸上のZバーの水準で垂直になり、
最適な水準(量)は一意(ユニーク)に決まる。
教科書ではその話はP130~P131で触れられていて、
5章の公共財の方でも同じ話があり、P148の図5-2と文章が該当する。
詳しくは章末の練習問題4-4に回されていて、上記のサポートウェブに解答がある。
いつかサイトが無くなったときのために、解答を引用しておくと、
「Zの需要に所得効果が存在しない場合,任意の値にZが固定されている限り,
Xの値がどのように変化しようが,限界代替率(無差別曲線の傾き)は変化しない。
ある配分で両者の無差別曲線の傾きが等しければ,その配分で与えられるZの値では,
Xがどのような値をとろうとも,両者の無差別曲線は等しくなる。
つまり,無差別曲線の傾きが等しくなる配分は横軸で測られた,そのZの値から伸びた垂線と等しくなる。」
本ノートの後ろの方に書いているコースの定理の章で詳しく述べるが、
図4-10については、契約曲線KK’が垂直でないために、
権利の配分次第で、効率的な資源配分の水準が変化する。
Aに喫煙権がある場合は、Z3~Z4の範囲、
Bに綺麗な空気を吸う権利がある場合は、Z1~Z2の範囲が、効率的な資源配分の水準となる。
どちらもパレート効率的ではあるが、資源配分の水準自体は、権利配分の仕方で変化している。
コースの定理によれば、どのように権利配分しても、民間同士の自発的な交渉(取引)によって、
政府が何をしなくても、勝手にレンズ内のコアのどこか(=パレート効率性)は実現し、
かつ、(所得分配の結果には影響を与えるが)資源配分は「不変」であるはずだった。
しかし、取引費用がゼロで交渉可能であっても、上記のように、Zの需要の所得弾力性が0じゃない限り、
もはやコースの定理は成立しない。準線形選好の仮定が必要なのである。

図4-11は、ピグー税やピグー補助(定額じゃなくて定率じゃないとダメ)が課されると、
予算制約線の傾きが変化する。
ピグー税の場合、Aから徴収された税は、全額Bに所得移転されることにも注意。
Aに補助金を与える場合には、Bから徴収することになる。
外部不経済のある財Zにピグー税だとS’に、外部経済でピグー補助金だとS’’になるから、
柴田のダイアグラムで、個人Aの予算制約線は、前者だとHJ’に、後者だとHJ’’になる。
外部性については、取引費用が0ならば、ピグー課税やピグー補助金を用いなくても、
当事者同士の交渉によって自発的にパレート効率的な資源配分は実現する。
しかし取引費用が大きく、交渉が不可能なケースについては、次の図4-12のように、
上手くピグー税やピグー補助金によって、外部性を内部化させてやらないと、パレート改善できない。

これまでの話は、喫煙家のAと、嫌煙家のBの2人だった。嫌煙家がBとCの2人に増えた場合、どうなるだろうか?
もしBがAにお金を払って喫煙量(排煙量)を減らしてもらった場合、Cはそれにフリーライドできる。
お互いフリーライドしようとした結果、交渉によるパレート効率的水準はもはや実現しない。
パレート非効率的な状態がナッシュ均衡となってしまう。
権利を確定するだけではダメで、そのような状況は公共財と同じとなる。
公共財は自発的にパレート効率性を実現するのは不可能なので、政府が必要になる。それを次で説明しよう。
○ 5章、公共財
・ 5章3節、公共財の自発的供給(拠出均衡)
個人Aの自発的な公共財の供給量(拠出量)をgA、個人BのそれをgBとすると、
公共財の供給量:gA+gB=G → gA=G-gB ・・・5.4
個人Aの予算制約:xA+pgA=MA → xA+pG=MA+pgB ・・・5.3
ファイル07のP32は、教科書とはちょっと記号が違う。
ファイル07では、5.3式のpgBの部分を、pg-Aと表記している。
以下、教科書の方の記号で説明する。
さて、5.3式で注意すべきは、Bの公共財供給量(拠出量)gBに応じて、Aの予算制約が変化すること。
AやBにとっての5.3式は、それぞれの個人所得(MAやMB)と区別して、完全所得と呼ぶ。

図5-3の上側は、一般的な無差別曲線の図で、予算制約線のうちMAQ3の水平線より上の破線部分は、
Bによって拠出された公共財を消費するしかないので、Aにとっては選択できない(私的財を消費できない)。
私的財も公共財も上級財(正常財)ではあるが、Bが公共財を拠出し続けてくれて、
AにとってQ3まで行ってしまうと、AはMAのすべてを私的財の消費に使ってしまい、
それ以上は私的財の消費は増やせない。
図5-3の下側は、例えば横軸上でG3点では、斜めのOAG線から、q3点がある水平線までの垂直距離が、
Aの私的財の消費量xAとなる。
その時のAの完全所得は、MA+pgB3であり、上の図より個人所得MAは、私的財xAの消費で使い切っており、
公共財の総供給量はG3(=gB3)となっている。

図5-4で、MBの高さにある水平線で、gA3という記号になっているのは、
Aの拠出金はpgAで、それがBにとっての縦軸上での予算制約線のシフト幅になるのだが、
予算制約線そのものは-pの傾きなので、pgAをpで割れば、横軸の変化となるためだ。
(y=-pxからy=-px+pzと縦軸切片が変化すれば、y=-p(x-z)と横軸切片はzになる。)
図5-3のq0~q3と、図5-4のE0~E3は、それぞれAとBの所得-消費曲線となる。
両者の図を合わせれば、図5-5となる。

図5-4のE3からE4への水平移動は、もうすでにBにとっての個人所得MBは、
全額私的財の消費に使ってしまっているので、それ以上Aが公共財への拠出を増やしてくれても、
その増やしてくれた分は、そのまま公共財の消費に用いるしかないためだ。
q3やE3までは、相手の公共財拠出の増加に伴うこちらの予算拡大によって、
私的財も公共財も上級財なので、両財とも消費を増やす。
予算拡大とは言っても、個人所得はそのままなので、それなのに私的財の消費を増やしているということは、
相手の公共財の拠出増加に対して、こちらの拠出は少し減らしていることを意味する。
この辺の説明は、「土居丈朗 入門公共経済学 日本評論社 2002/11」
2章3節、P31の図2-5と、P32-P33の文章がまさにピッタリなので、そちらで説明しよう。

予算制約線:xA=-pG+MA+pgB ・・・5.3
予算制約線の角度がpということは、横軸で1単位動けば、縦軸でp単位動くことを意味する。
MAF=pgB → MAI=gB=OJ
線分OF:Aの完全所得
Bの拠出金(負担金)pgBを所与として、Aは最適消費水準Eを決定する。
線分OK:Aの欲する最適な公共財の総供給量G
線分JK:gA
さて、MAとpは不変として、gBが増えたとしよう。
Aにとって実質所得の増加に等しく、予算制約線は右上にシフトする。
私的財も公共財も上級財なので、新しい均衡点E’は図2-5Bのようになる。

予算制約線:xA=-pG+MA+pgB’ ・・・5.3’
MAF’=pgB’ → gB’=OJ’
gBの増加分=JJ’
線分OF’:Aの完全所得
線分OK’:新しくAの欲する最適な公共財の総供給量G
線分J’K’:gA’
予算制約線のシフト幅=FF’=Aにとって実質所得の増加分
に対してE’点では、その全額を公共財の消費には充てていない。
私的財も上級財なので、私的財の消費量も増やしている。
MAが不変の中、xAを増やせば、その分だけAの拠出量は減り、gAからgA’に、JKからJ’K’になる。
図2-5から類推すれば、逆にBが公共財供給量を減らせば、Aにとっての実質所得の減少となり、
私的財の消費量を減らしつつ、Aの拠出金pgAは、逆に若干増えることになる。
このような現象や効果は、他の学問でも文章だけで説明されたりしているのかもしれないが、
無差別曲線を使った図解は、ミクロ経済学の真骨頂だと思う。
林公共に戻ろう。図5-5では、お互いの所得-消費曲線の交点(S点)が、自発的供給(拠出均衡)となる。
拠出均衡はナッシュ均衡ではあるが、パレート効率的ではない。
S点より右下のレンズは無差別曲線同士で作られ、S点からその内部への移動はパレート改善となる。
外部性とは違って、公共財の場合、お互いがフリーライドしようとするので、
交渉によってパレート効率性が実現(コースの定理)することはない。ナッシュ均衡なので自分からは動かない。
S点は、必ずパレート非効率的となる。なぜなら、S点でのお互いの無差別曲線の傾きを考えると、
VAの傾きは必ず0(水平)であり、IBの傾きは必ず-pだからである。
・ 中立定理(必ず成立するとは限らない=重要)

図5-6、拠出均衡(S点)の状態から出発して、BからAへと所得移転(⊿M)を行っても、
拠出均衡点はS点のままで不変となる。それを中立定理という。
AとBの効用関数自体が変化しない限り、Aの個人所得の予算制約線(JH→J’H’)も、
Bの個人所得の予算制約線((JC→J’C’)も、その傾きは等しいままなので、
それぞれの所得-消費曲線は、始点が変わるだけとなる。
Aの所得-消費曲線の始点は、q0→q0’に、
Bの所得-消費曲線の始点は、E0→E0’に、なるだけ。
ワーの中立命題(P.G.Warr 1983)とも言われる。土居公共の2章4節(3節ではないことに注意)や、
井堀利宏 財政 (現代経済学入門) 岩波書店 などにも載っている。土居公共の2章4節の方が詳しい。
公共財は等量消費可能なのでGの水準は不変だが、費用負担の拠出は変化する。
(従って、拠出均衡が不変という言い方は、誤解を招くような気がする。確かに均衡点Sは不変だが。)
BからAへ所得再分配が行われれば、Bはその分だけ公共財への(拠出金)を減らすが、
逆にAが増加させて相殺する。結果、公共財の総供給量Gは変化しない。
例えばAで言えば、斜めのOAZmax線から、拠出均衡のS点までの距離は不変なので、私的財消費量は不変。
しかしBから所得移転⊿Mを受けているので、拠出金pgAを増やしていることになる。
pgAの増加量は、他方で同じロジックでBが減らしているであろうpgBの量となる。
図5-3の下の図と、図5-6を併せて見れば分かるように、
中央の水平線(J’H’)から最適消費点までの距離が、Bの拠出金pgBだからである。
そして、拠出均衡のS点は不変なので、無差別曲線も移動していないので、効用水準も変化しない。
ちなみに中立定理(中立命題)は、次の文献によると、
Warr(1983)より以前に、Sibata(1971)で暗黙のうちに導出されていたとのこと。
「フィナンシャル・レビュー / 財務省財務総合政策研究所 編 75号 2005年
井堀 利宏 国際公共財の供給と各国の経済厚生」
上記の文献および、上記の井堀財政にも載っていて面白いのが、トランスファー・パラドックス。
日本、アメリカ、ドイツ、それぞれの防衛費に関して自発的供給のナッシュ均衡になっているとしよう。
アメリカ:全世界の防衛費に興味。
日本:アメリカと日本(太平洋)だけに興味。
ドイツ:アメリカとドイツ(大西洋)だけに興味。
アメリカの防衛費=純粋公共財、日本とドイツのそれぞれの防衛費=準公共財。
「交易条件は一定」として、日本からアメリカへ所得移転(トランスファー)が起きると、
日本は防衛費を減らし、アメリカは防衛費を増やす。両国だけを見れば私的財の消費量を含めて経済厚生は不変。
ところが、アメリカの防衛費の増加は、ドイツにとって経済厚生を高める。
ドイツにとっての公共財の総供給量Gの増加は、ドイツの実質所得の増加となる。
その結果、ドイツは私的財の消費量を増やし、防衛費を減らす(上記の土居公共の2章3節の分析が該当)。
結局、ドイツがフリーライドするわけだが、これはアメリカの経済厚生を低下させる。
ドイツが拠出を減らすので、アメリカにとって実質的な所得の低下となり、私的財の消費を減らしつつ、
ドイツが減らした分の「一部」を埋め合わせるように、アメリカはさらに防衛費を増やす
(これも上記の土居公共の2章3節の分析が該当)。
この副次的なアメリカの防衛費の増加は、日本の経済厚生を高める。
そうすると、日本がアメリカに所得移転してあげた立場なのに、
アメリカの経済厚生は低下し、逆に日本の経済厚生は高まる結果となる。
「交易条件は一定」としたが、この交易条件効果を考慮すると、国際貿易論の話となる。
トランスファー問題と言われ、有名なのがケインズと(ヘクシャー=オリーン・モデルの)オリーンの論争。
さて、林公共に戻ろう。中立定理は必ず成立するとは限らない。
所得移転(⊿M)によって、個人Aの当初の予算制約線JH(個人Bの当初の予算制約線はJC)が、
J’H’へと(個人BのはJ’C’へと)下方シフトするが、当初の拠出均衡点Sより下に来てしまうと、
拠出均衡はS’点になってしまう。それを示すのが次の図5-7。

図5-6で言えば、図の中央にある水平線から拠出均衡点までの垂直距離が、Bの拠出金であるpgBとなるので、
所得移転(⊿M)によって予算制約線が下方シフトすれば、その分だけpgBが自動的に減る。
ところが、拠出均衡点を越えて予算制約線が下方シフトしてしまうと、pgBがマイナスとなってしまう。
井堀財政でも、中立命題が成立しない理由が文章だけで説明されており、
公共財の負担量が負になりえないとのこと(非負制約)。
所得再分配をやり過ぎて、最初の拠出均衡の水準に対する費用支払いができないほど、
Bの所得が無いという意味では、所得制約(予算制約)とも言える。
ちなみに、中立定理が成り立つにしろ、成り立たないにしろ、どちらも需要の所得効果の話とは関係ない。
そもそも拠出均衡の点Sや点S’はパレート非効率的で、
どちらもパレート効率的な水準となる契約曲線上(図5-5のKK’曲線)とは違う所にある。
そのとき(違う所にあるとき)、契約曲線が垂直であるかどうかとは関係ない。
・ 5章4節、拠出均衡とクラウディングアウト。
まず、すでに拠出均衡が成立していて、ある程度の公共財をすでに自発的に供給している状態から出発する。
その状態から、政府による課税と、その租税収入を原資とした公共財の供給を政府が直接行うと、
その分だけ民間による自発的な公共財供給が減少し、完全にクラウディングアウトする(均衡点はSのまま)。
その際の重要な仮定が、図5-6の所得移転と同じ効果となるように、課税方法を「定額税」とすること。
「定率税」だと、予算制約線の傾きそのものが変わってしまう。
このクラウディングアウトに関しては、教科書の方では文章による説明だけしか無いが、
講義ノートの方では、ファイル07のP39~P42で、定式化と図解が行われている。
いつ無くなるかわからないので、ここもノートを取っておこう。
AとBからの徴税:TAとTB
政府による公共財供給(実質):gG
政府の予算制約:pgG=TA+TB → gG=(TA+TB)/p
5.3式と5.4式(公共財の供給量:gA+gB=G)より、
課税前の個人Aと個人Bのそれぞれの予算制約式は、
個人Aの予算制約:xA+pgA=MA → xA+pG=MA+pgB
個人Bの予算制約:xB+pgB=MB → xB+pG=MB+pgA
それぞれの予算制約式にTAとTBを課税すると、



図5-6の中立定理と同様に、AとBの所得-消費曲線の始点が変わるだけで、拠出均衡点Sは不変である。
ただし、クラウディングアウトが発生しないケースも考えられる。
章末の練習問題5-4で、解答は上記サポートウェブ。それによると、答えは図5-7の事例である。
図5-7では、Bは公共財を供給していない。
JJ’’に相当する所得移転(⊿M)をAは受けており、自分の所得-消費曲線に従って、
最適な公共財の量(S’)をすでに自発的に供給している。
Bに公共財を供給してもらって(gB)、Aの実質所得が増加している形ではなく、
Bから所得移転を受けて、Aが自身で拠出していることになる。
一方、Bの最適消費点はS’なので、Bにとって最適な公共財の消費量は、
すでにAが供給している公共財の総量で十分賄えている。
ちなみに、図5-7のS’点は、図5-4で言えばE4点に相当する。
そのBに課税しても、Bが公共財の供給を減らすことはない(そもそも供給してないから)。
さらにAの所得-消費曲線は右下がりなので、最終的に公共財の総供給量は増えている(公共財も上級財だから)。
というのも、A自身が政府の人間だったとしよう。
実質的には所得移転と同じだが、名目上はMAは不変だし、かと言ってBから徴収した税を、
MAとして勘定してしまうと、さすがに横領となるw
勘定はしないが、A個人としての公共財供給gAは減らして、私的財の消費(は上級財なので)に充てれば、
Bから徴収した税があるので、それを当てにして、政府による供給を加えた公共財の総供給量を
最適消費として増やすのが、Aにとって最適。
クラウディングアウトしている話に戻そう。
マクロ経済学的な発想で、クラウディングアウトは悪いというイメージがあるが、
上記の話はそれだけでは個人的に問題だとは思えない。民間投資をクラウディングアウトしているわけじゃないし。
結局AとBが社会契約を結んで、「政府」という肩書きを作っただけで同じ公共財を供給しているだけの話だし、
どちらにしろ拠出均衡(S点)自体がパレート効率的ではない。
S点から右下のレンズ内に移動するように政府が公共財を供給でき(社会契約を結べ)れば、パレート改善である。
では、そのパレート効率的な公共財の水準を、実際に政府が供給できるのかどうか、そのメカニズムが問題となる。
上記のように、所得のみに影響を与える「定額税」だと、政府による公共財の供給はパレート改善できない。
公共財の価格に影響を与える「定率税」が必要となる。人頭税のような定額の固定税だと、上手く行かないのである。
そこで同じ5章4節のクラウディングアウトの続きとして、P162より、リンダール・メカニズムの話となる。
ちなみに、地方交付金のような政府間財政移転だと話は逆となり、歳出とは独立の定額が望ましい。
その話題については、講義ノートのファイル10を参照。歳出に比例するような「定率」の交付(ピグー補助)は、
地方公共財のスピルオーバーなどの外部性があるときには望ましい。
・ 5章4節の続き、リンダール・メカニズム。
リンダール・メカニズムは、公共財の需要量に応じて負担率tが決まる受益者負担のメカニズムである。
AとBの2人経済ならば、tと1-tになる。あるtの値の下で需要を表明させて、
両者の需要量が一致するまでtの値を変えては表明を繰り返す。
一致すれば、パレート効率的となるサミュエルソン条件も成立する。
またtの値が決まれば、AとBがそれぞれ直面する公共財価格は差別価格となる。
私的財(ニュメレール)をX、公共財の(相対)価格をp、所得をMとすると、
Aの予算制約式:Xa+tpG=Ma
Bの予算制約式:Xb+(1-t)pG=Mb
公共財の限界費用を一定として、負担率×限界費用=tpはAが直面する租税価格といい、
リンダール均衡が成立したときの租税価格をリンダール価格という。
次にAとBにとっての効用最大化条件(相対価格=限界代替率)は、
A:tp=MRSa(Xa,G)=MRSa(Ma-tpG,G)
B:(1-t)p=MRSb(Xb,G)=MRSb(Mb-tpG,G)
最終的に公共財の需要量が等しくなれば、公共財は等量消費可能なので、G*=Ga=Gbであり、
tp+(1-t)p=pである以上、左辺の1項目にAの最適化条件式、2項目にBの最適化条件式を代入すると、
MRSa(Ma-tpG*,G*)+MRSb(Mb-tpG*,G*)=p ・・・サミュエルソン条件
このリンダール・メカニズムも、柴田のダイアグラムで分析できるのが面白い。
(柴田公共では5章のP162~P165。)

図5-9では、まずAの負担率がt=1だった場合、Aの予算制約線はJHのままである。
そこから、負担率が下がれば、図4-11でピグー補助をしてもらってるのと同じになるので、JH’になる。
定率税により価格が変化しているので、価格-消費曲線と言える。
一方、Aの負担率がt=1のとき、Bの負担率は1-t=0なので、負担をしないことを意味する。
Bの予算制約線もJHとなる(重要)。
柴田のダイアグラムにおいてBは、無差別曲線図をそのまま描いていることを思い出そう。
本来なら予算制約線は右下がりだが、BにとってGの価格は0なので、J点の高さで水平となる。
Aの負担率が1から下がれば、Aの最適消費点は、q0からq’に、BはE’’になる。
両者の公共財需要量は一致していない。特にBが多すぎて、Aが少ない。
リンダール・メカニズムに従って、さらにAの負担率tを下げて行くと、
L点で両者の無差別曲線は接していて、リンダール均衡という。
価格調整による均衡が、パレート効率的であるという意味で、準市場的であり、
図5-5の拠出均衡よりもパレート改善していることがわかる。
追記。リンダール・メカニズムでは、負担率(および租税価格)に対して公共財需要量は変化する。
結果的に、AとBは等量消費になり、サミュエルソン条件も成立する。
これは、公共財の最適供給量が一意に決まるための条件として、
公共財需要の所得効果が0であるという条件は必要なのだろうか?
準線形効用関数の場合、所得効果は発生しないので、価格が変化した場合、発生するのは代替効果のみとなるが、
関係があるのだろうか?結論。必要ないし関係ない。
まず準線形効用関数は、「所得」が変化した時に無差別曲線および最適消費点がどのように動くか
についての話であって、リンダール・メカニズムで動いているのは「価格」である。
そしてサミュエルソン条件の成立というのはパレート効率的になるだけの話であって、
別に最適供給量が一意に決まることまで、言ってるわけではない。
逆に言えば、所得分配次第で、任意のパレート効率的資源配分を実現できる。
「厚生経済学の第二基本定理:適切な所得分配(初期保有量の分配)を行えば、
その後は競争均衡によって、任意のパレート効率的資源配分を達成できる。」
次の柴田公共のP154とP168より、リンダール・メカニズムは、第二定理とよく似ているとのこと。
次の次の板谷公共のP135より、問題点として、公共財が下級財のケースでは、
所得が増えて高所得者になった場合、かえって公共財への需要が減るので、負担率が逆に下がってしまうとのこと。
高所得者ほど安全・医療・道路・公園などについて自分で賄えるため、政府が直接供給する公共財については、
低所得者の方が需要が大きくなる。リンダールメカニズムで求める費用負担の割合は、逆進的になる。
○ 5章5節、メカニズムデザイン。6章、内容は公共選択論。
リンダール・メカニズムには、真の需要顕示のインセンティブが無く、虚偽報告する可能があるので、
続いてメカニズム・デザインの話に移る。
クラーク=グローブス・メカニズムや、林公共ではヴァリアン・メカニズムも説明される。
前者については、柴田公共ではよく考えられた数値例で詳しく説明されるが、奥野ミクロの簡潔さも素晴らしい。
6章の公共選択論については、専門書はまだ読んだこと無いが、
公共経済学の教科書の中では、次の柴田公共が個人的にベストだった。
林公共の6章で面白かった、P196~P201の、直接民主制と間接民主制のパラドックスについて、
林の講義ノートの方には無いみたいなので、
オストロゴルスキーのパラドックス(逆説)と、コラム10の漸進的改革vsビッグバン改革の話を、
雑記ノートの方で。
○ 7章、地方分権と政府間財政関係(租税競争)。
・ まずはP213~P215、ヘンリー・ジョージ定理と資本化仮説。
ヘンリー・ジョージ定理:都市人口が最適規模である時、地代と地方公共財の費用が等しくなる。
効用関数U(x,g)で、xは私的財、gは地方公共財。
生産関数f(n,l)で、nは人口、lは土地。土地は固定的な生産要素なので簡単にf(n)とする。
資源制約は、xについては人数分消費されるが、gについては等量消費が可能なので、f(n)=nx+g。
これをg=f(n)-nxとして効用関数に代入。
U(x,f(n)-nx)をnで微分してゼロと置いて最適化条件を導出。その際、合成関数の微分となる。
∂U ∂U ∂g ∂U
───=───・───=───・[f'(n)-x]=0 → 1階の最適化条件式:f'(n)=x
∂n ∂g ∂n ∂g
人口のnで微分しているということは、最適人口を求めていることになる。
そして地方公共財を対象としているので、この最適化条件式は人口移動を前提とした最適人口規模を意味する。
左辺の方が大きければ、生産量の限界的な増加に対して、人口流入に伴う限界的な私的財の消費増加量は小さい。
従って、地域人口を増やすべきとなる。その逆は減らすべきとなる。
一方、生産関数が1次同次ならば、オイラーの定理(完全分配定理)が成り立つ。
すなわち、規模に関して収穫一定の場合、利潤は常に0であり、生産物(収入)は生産要素に分配され尽くす。
経済数学ノートの 「21:オイラーの定理」を参照。
また利潤最大化の条件から、労働の限界生産力=実質賃金(f'(n)=w)。
地代の合計をRとすると、f(n)=nw+Rと分配され尽くすので(省略したが、本来はf(n,l)なので)、
R=f(n)-nw=f(n)-nf'(n)=f(n)-nx=g。
すなわち、R=gとなるが、最適人口規模が達成されている状態では、
結果的に地方公共財の費用と地代は等しいことを意味するだけで、
議論を逆さまにして、地代に100%課税(結局は国有化)すれば、
地方公共財の供給量が自動的に最適になるというわけではない。
資本化仮説:地方公共財の供給増がもたらす限界便益の総和は、すべて地代(つまり地主)に帰着する。
以下は、次のファイルを参考にする。
http://repository.osakafu-u.ac.jp/dspace/bitstream/10466/10434/1/2010900034.pdf
要約を先に述べると、人々の選好が同質、移動が自由、などの一定の条件が成立するとき、
借地・借家・賃貸マンションなどの借り手にとっては、地方公共財の増加に伴い、
人口流入による地価や賃貸料の上昇によって、最終的に効用の純増は起きないからだ。
本ノートの一番最初の「財政学をつかむ」の章で紹介した教育バウチャーの話と似ている。
結局、人気校の周辺の土地は金持ちが買って地価が高くなり、貧乏人は人気校に行けない。
消費財x(ニュメレール)、土地h、地方公共財g、
支払う地代R(xはニュメレールなので、Rは相対価格にもなる)、一括税τ、所得y、
家計(住民)の効用関数と予算制約式は、
_
効用関数:U(x,h,g)=u ・・・1
予算制約式:x+Rh=y-τ ・・・2
_
となる。uは、どの地域においても等しい効用水準で、
逆に言えば、足による投票によって、地域間の効用差が無くなるまで、家計は移動し続けることを意味する。
後は最適化(微分して0と置く)。 _
人口はnで一定、1人当たり土地需要h、土地の供給はHで固定。
_
土地市場での需給均衡条件:nh=H ・・・3
供給曲線が垂直で、土地需要の変化は、すべて地代の変化で吸収される。
裁定条件が成り立つように、地域間の効用差が無くなるまで(裁定機会が無くなるまで)、
地代という価格で調整されるのだろう。
実際に、効用関数を全微分して、dU=0と置けば、無差別曲線の限界代替率が求まるので、
予算制約式の方も全微分して、一定の所得の下なのでdy=0とすると、予算制約式の傾きが求まる。
その他の条件を一定として考えるので、まずは地方公共財の供給増だけの効果を見るために、dτ=0とする。
租税の効果は次のステップで考える。消費財xの限界効用をUxと表現すると、
Ux Ug
Uxdx+Uhdh+Ugdg=0 → dh=-──dx-──dg ・・・A1
Uh Uh
dx+hdR+Rdh=0 → dx=-(hdR+Rdh)・・・A2
限界代替率=予算制約式の傾きなので、A1式とA2式の連立方程式となる。A1式にA2を代入すると、
Ux Ux Ug
(1-──R)dh=──hdR-──dg ・・・A3
Uh Uh Uh
消費財と土地の2財の関係で言えば、x-h平面での家計の効用最大化の1階条件から、
Ux/Uh=Rとなるので、A3式の左辺=0となる。さらに次のような概念と記号を定義すると、
地方公共財の限界的な供給増に対する、地代の増加量=地代勾配=dR/dg=Rg
dR 1 Ug
───=Rg=──・── ・・・4
dg h Ux
3式を代入すると、
Ug _
n・──=Rg・H ・・・5
Ux
地方公共財の限界効用(限界便益)の総和=地代変化の総額
地方公共財を増やしたときに、増える効用の総和が、まるまる地代の増加量で吸収されることになる。
5式の左辺の分母にUxがあるが、ニュメレール(合成財であり、所得とも考えられる)の価格は、
基準化されて1だが、限界効用(Ux)については、準線形効用関数を仮定することによって一定にできる。
ただし上記の結論も、下記に続く結論も、別に準線形効用関数が必要条件というわけではない。
Ug/Uxの部分を、地方公共財の限界効用と表現してるだけ。
上記は、租税の効果を0(dτ=0)としているので、UGは粗限界便益という。
租税負担を考慮しないグロスの限界効用で、考慮すると純限界便益となるので、次のステップに移ろう。
租税効果を考慮して、さらにGの費用関数c(g)を導入し、地方政府の予算制約式、nτ=c(g)も加えると、
サミュエルソン条件が成立することを示そう。
その際に、地方政府は地代が最大になるように地方公共財を供給するとし、地代勾配=dR/dg=0となる。
A1式はそのままだが、改めて家計の予算制約式と、地方政府の予算制約式を全微分すると、
dx+hdR+Rdh=-dτ → dx=-(hdR+Rdh+dτ)・・・A4
dτ c'(g)
ndτ=c'(g)dg → ───=────・・・A6
dg n
まずA4式を、A1式に代入すると、
Ux Ux Ux Ug
(1-──R)dh=──hdR+──dτ-──dg ・・・A7
Uh Uh Uh Uh
相変わらず、家計の効用最大化の1階条件からUx/Uh=Rとなるので、A3式の左辺=0となる。
dR 1 Ug 1 dτ
───=──・──-──・── ・・・A8
dg h Ux h dg
これに3式を代入すると、
_ dR UG dτ
H・───=n・──-n・── ・・・A8
dg Ux dg
さらにA6式を代入し、dR/dg=Rg=0を利用すると、
_
H・Rg=n・(Ug/Ux)-c'(g) → n・(Ug/Ux)=C'(g)
地方公共財の限界効用の総和=限界費用 (サミュエルソン条件)
本来であれば、地方公共財は受益者負担の原則が望ましいが、そうはならないことを示すのが資本化仮説。
地主が人気の地方公共財を望み、ゴミ処理場のような不人気な地方公共財を嫌う理由がよくわかる。
だからと言って、上記の結論だけで勝手に地主を憎んではいけない。
大切なのが実証で、地方公共財の便益が、どの程度地価や家賃に反映されているのか、
資本化を確認して「開発利益の還元」を模索しなければならない。
・ 7章2節、政府間財政関係(租税競争)。
ティブーの足による投票仮説は、政府間の競争(資本や労働力となる住民の獲得)を通じて、
公共財に対する選好の顕示が上手く示されて、市場均衡的にパレート効率性が実現できると考える。
しかし、政府間で企業や工場、優秀な人材を奪い合うために、それらに課される税率は過度に引き下げられる一方、
その地域に固定的な労働や土地などには、過度に税負担が重くなることがよくある。
租税競争と言って、公共財を非効率的な水準に過少供給してしまう可能性がある。
ティブーの足による投票仮説が成立するための詳しい条件については、次の柴田公共のノートで説明。
オーツと言えば地方分権化定理だが、一方で上記のような「底辺への競争」という懸念も示していた。
分権化定理は、公共財の供給量を20望むグループと、40望むグループがいるとき、
画一的に平均値である30を供給すると、両グループとも10の分だけ厚生がマイナスになる。
20と40をそれぞれ供給する地域があった方が望ましいという話。
オーツの懸念をフォーマルに検証する研究が、ウィルソン(J.D.Wilson)らによってなされた。
詳しい分析は、次の次の板谷公共の所で行うので、用語の定義だけ先に。
直接的財政外部性=スピルオーバー。地方公共財の便益が、その他の地域にも及ぶこと。
水平的財政外部性(間接的財政外部性)=
A地方が税率を上げると、B地方へと労働や資本が流れ、Bの税収が増える(外部経済)。
AはBでの外部経済まで考慮せずに税率を上げるので、税率を上げることの費用については
逆に過大に見積もってしまう。結果として、地方政府の設定する税率は過少となる(租税競争)。
垂直的財政外部性=
課税ベースが同じ場合、国税+地方税なので、国が国税を上げちゃうと、地方は何にもしてないのに税収減。
後でもう1度触れるが、同じ課税ベースに対して参入するので、
共有地の悲劇(つまりクールノーモデル)と同じ構造となる。
同じ課税ベースに対して、国と地方の競合に関する話なので、資本や労働が移動することを通じた、
間接的な外部効果ではない。
○ 10章の公的扶助と、12章の年金。
ちょっと長いので、いったんここで区切って、本ノートの最後に回そう。
● 「柴田弘文 柴田愛子 公共経済学 東洋経済新報社 1988/12」
1つ上の林公共の最初で説明したように、林公共の4章外部性、5章公共財で、
柴田のダイアグラムを使って説明しており、林公共の方が簡潔に説明していてわかりやすい。
もし柴田公共を読む予定ならば、先に林公共の4章と5章を読んでおこう。
○ P84~P87の、生産可能曲線(PPF)の非凸性

X財の生産によって公害(工場が川を汚染)が発生し、Y財(農業)に被害が及ぶとしよう。
その場合、そのような外部性が無いときと比べて、生産可能曲線(PPF)は横軸の切片が原点方向にシフトする。
しかし縦軸の切片は、公害を発生させるX財の生産がゼロなので、Y軸の切片は凹まない。
外部性が無いときのPPFの横軸切片をR、外部性によって凹んだときの横軸切片をSとすると、
SR上でもX財は生産可能となる。
その場合、凹んだPPF上で、X財とY財を両方生産するより、
凹む前の外部性が無いかのようなPPF上に位置することになるR点でX財だけを生産した方が、
かえって社会厚生は上昇する。
もうY財は生産されていないので、ある意味外部性が発生しておらず、川を農業用水用に清浄化するより、
工場排水のための下水として使ってしまった方が望ましいということもありえる。
色んな教科書を読んでいると、凸性と内点解を安易に仮定してその話だけで終わることが多いが、
現実には非凸性と端点解(コーナー解)の問題はとても重要。
○ P87~P94、共有地の悲劇
次の板谷公共で、柴田公共の説明も加えて一緒に説明。
○ 非競合性と価格差別(4章および5章)
4章1節のP141より、非排除性のある財は、等量消費せざるを得ないのに対して、
非競合性のある財は、等量消費が「望ましい・すべき」という違いがある。
非競合性のある財は、追加供給に対する限界費用がゼロなので、
価格をゼロにして、お金を払わない消費者も参加させるべきとなる。
4章2節、非排除性がある場合は、フリーライダーが起きる。
自己の需要を顕示し、支払意思を表明しないので、供給も過少供給となる。
では、排除性があれば市場供給量はパレート効率的になるかというと、
排除性があっても競合性が無ければ、やはり過少供給になる。
限界費用がゼロならば、価格もゼロにして消費させればパレート改善するからである。
ミクロ経済学を勉強していると、もはや操業停止点より上の限界費用曲線=供給曲線にしか目が行かないが、
仮に固定費用が賄えない場合、そもそも供給されないという問題が発生してしまう。
一般的に最適化条件である価格=限界費用(P=MC)ばかりが強調されるが、
固定費用の存在および平均費用が逓減している区域が見過ごされがちである。
排除性があり、さらに市場供給が可能であったとしても、非競合性がある場合、
一律の入場料を課して払える人だけに消費させるのは、パレート非効率的である。
そこで差別価格を用いることで、消費者をもっと増やすことができ、パレート改善できる。
するとその財は、排除可能であっても、租税(差別価格)で賄い、あたかも非排除性(と非競合性)のある
公共財として供給することが望ましいことになる。さらに詳しい説明と数値例が、次の5章。
ここから5章。個人的に本書の中で一番好きな章が、5章の準公共財。
クラブ財と地方公共財が有名で、どちらも排除性はあるが競合性はない。
前者だとスポーツクラブの例が有名で、会員制にして排除することは可能だが、
施設内の設備を利用するにあたっては、混雑しない限りは競合性はない。
地方公共財の場合には、地理的に排除性が成立する。
5章2節、平均費用逓減財と非競合性はパラレル。
規模の経済が働くと、利潤最大化の下では独占価格が付けられ、パレート非効率的(過少供給)になる。
さらにP194の下から12行目からの説明が、個人的に目からウロコだった。

独占市場で、限界費用がゼロの場合、M点で供給量が決まり、独占価格はPとなる。
独占企業の収入は、原点Oから始めて□OMLPの長方形となる。
限界費用0なので、そのまま生産者余剰となる。
もし完全競争市場ならば、P=MCより価格は0、総余剰は三角形ODD’となり、
生産者余剰は0なので、総余剰=消費者余剰となる。
独占によって価格はPに上昇し、総余剰はODLMに減少するだけでなく、
総余剰に占める消費者と生産者との分配(割合)も、消費者が不利となり、生産者に有利となる。
さて、もし平均固定費用曲線(AFC)が、L点の下側を通るなら、固定費用を賄える。
ところが、もしAFC’がL点の上側を通るなら、固定費用を賄えないので、そもそも市場に供給できない。

では、このような財は供給すべきではないのだろうか?
この独占企業の総費用は、□OMG’F’の長方形となる(限界費用はゼロなので可変費用もゼロ)。
一方、消費者余剰は、△ODD’というでっかい三角形になる。
もし△ODD’の面積が、□OMG’F’の面積よりも大きいならば、
この財を供給することによって正の社会的余剰が生まれる。
(混雑するまでの)非競合財は、限界費用がゼロである以上、とりあえず全員に無料で提供し、
消費者余剰(パイ)を最大にするパレート効率的水準を実現しておいて、
その中から固定費用を別途徴収すればいい。その徴収方法は最大化された消費者余剰の分配問題に過ぎない。
平均固定費用を消費者から一律に徴収する方法もあるが、その場合、上記のように市場供給されない場合もある。
しかし、4章2節のP145~P147にもあるように、一物一価にする必要は無く、
独占市場でおなじみの価格差別を用いる方法もある。その数値例が5章2節のP195~P198にある。
マイクロバスのチャーター料が2200円で、次の表5-B
| 留保価格 | 費用分担 |消費者余剰|
──────────────────────
A| 550円 | 500円 | 50円 |
B| 500円 | 450円 | 〃 |
C| 400円 | 350円 | 〃 |
D| 350円 | 300円 | 〃 |
E| 300円 | 250円 | 〃 |
F| 250円 | 200円 | 〃 |
G| 200円 | 150円 | 〃 |
──────────────────────
|2550円 |2200円 | 350円|
1人当たり平均費用を一律に課すような価格設定だと、上記の数値例では市場供給されない。
2人で分配=1人当たり1100円
3人で分配= 〃 733円
4人で分配= 〃 550円
5人で分配= 〃 440円
6人で分配= 〃 360円
7人で分配= 〃 314円
しかし、支払意思額である留保価格の合計は、2550円でチャーター料を超えている。
そこで、表5-Bのように費用分担(価格差別)することにより、供給可能(パレート改善)となる。
○ 価格差別の種類
第1種価格差別:1人1人の留保価格を完全に知っているので、1人1人に異なる価格を設定
第2種価格差別: 〃 を完全には知らないので、消費量ごとに異なる価格を設定
第3種価格差別: 〃 を完全には知らないので、グループごとに異なる価格を設定
・ 第1種価格差別(完全価格差別ともいう)
表5-Bは、需要曲線とも考えられる。このケースでは消費者余剰を全て吸収することができる。
面白いのが、このケースではMC曲線より上はすべて生産者余剰となるので、
留保価格=限界費用となる個人まで財の供給が行われ、死荷重損失は発生しない。
個人個人の留保価格を完全に知っているというケースは、現実的にはなかなかあり得ないが、
一番近い例として、僻地の医者がある。
同一の医療サービスに対して、金持ちから多く取り、高価格を提示。貧乏人には逆に低価格を提示。
平均費用価格を一律に提示すると、固定費用が賄えず、医療サービスそのものが提供できなかったのだろう。
負担の不平等は、高負担を課せられた者にとってもパレート改善で効用を高める。
また、独占市場と価格差別の理論における一般的な注意点として、再販不可能な財に限られる。
再販可能であると、価格差を利用して裁定取引が起きるからだ。
逆に言えば、再販可能な非競合性のある財は、たとえ排除可能であったとしても、やはり市場供給は困難となる。
非市場的なコスト負担方法が必要となる。
・ 第2種価格差別
代表的なのが、スーパーなどでの大量購入割引、抱き合わせ、二部料金制。
次の第3種価格差別で説明するように、価格弾力性が大きい人ほど、値段が下がったら消費量を大きく増やすことと、
結果は同じになっているが、仕組みはまったく違う。
第1種や第3種のように、個人やグループで需要曲線(留保価格や価格弾力性)を、企業が識別するのが困難なので、
価格と数量の組み合わせが違うメニューを提示し、消費者に「自己選択」させていることになる。
自己選択メカニズムと来れば、参加制約条件と誘因両立制約条件である。
「ヴァリアンの入ミク(9版)の26章3節、P419~P422」では図解で、
「芦谷政浩 ミクロ経済学 有斐閣 2009、のP245」では数値例で、その説明があるが、
「柳川隆 吉野一郎 ミクロ経済学・入門―ビジネスと政策を読みとく 有斐閣 2008/03」
のP159~P164がオススメで、ノートかコピー必須。
参加制約条件と誘因両立制約条件を、これ程までに簡潔にわかりやすく説明したものは他に無いと思う。
ミクロ経済学ノートにもまとめた。
「抱き合わせ」、ヴァリアンの入ミク(9版)の26章5節、p424~p425。
共通に掛かる費用を削減できる。論文はいくつかまとめてホッチキスで留めて学術雑誌として売られる。
互いに補完財ならば、読む方としても効率が良い。
ワープロソフト 表計算ソフト
個人A 120円 100円
個人B 100円 120円
同じ会社Cが、それぞれのソフトを個別に売ってみよう。単純化のため限界費用は0とする。
ワープロソフトだけを売るなら、価格設定は100円にしないと個人Bまで買ってくれない。
表計算ソフトも同様に100円となる。会社Cの収入は400円となる。
ところが、抱き合わせ(パッケージ)にすることで、パッケージソフトの価格を220円にすれば、
個人Aと個人Bの両者とも買ってくれる。会社Cの収入は440円となる。
「二部料金制」。
まず、図1(MC=0)の場合、価格=限界費用で財をD'まで供給すると、
固定費用OJKD'の分だけ赤字となる。
二部料金制では、限界費用に等しい価格で財を供給しておき、発生する赤字については
基本料金(固定料金)を別途徴収する。
購入量をX、価格をPとすると、
支払い(E)=基本料金(F)+従量料金(PX)
1単位当たり支払は、両辺をXで割ると、
E F
──=──+P
X X
従って、消費者1人1人に対して同じ従量料金を提示するが、消費者にとっては購入量が増えれば増えるほど、
1単位当たり支払った価格は下がる。
二部料金制で有名なのが、電気・電話・ガス・水道などの公共料金や、遊園地(入園料と乗り物料)など。
http://tomoinoue.web.fc2.com/notes/notes.html
より、スポーツジムの数値例を引用。
会員(C)は、1日500円
非会員(N)は、1日1000円
ただし、使用日数をX、年会費6万円とすると、年間支払額Eはそれぞれ、
Ec=500X+60000 → Ec/X=500+(60000/X)
En=1000X → En/X=1000
使用日数1日当たりの支払価格が等しくなるときの、使用日数Xは、
500+(60000/X)=1000 → X=120
年間120日より多く利用する消費者は、会員になった方が得である。
スーパーの大量購入割引も同様で、大量購入した人でないと値引きを受けられない。
逆に価格弾力性の低い人は、値段を下げた所で大量購入してくれないので、
そのような人は元々、多少高かろうが安かろうが、少量しか欲しくないと思っている。
そのような人向けに、バラ売りで少量ずつ買えるけど単価は少し高いメニューが用意されている。
この第2種価格差別にも再販の問題が発生する。消費者間で転売可能だと、誰か1人が「まとめ買い」して、
みんなで分ければ、大量購入割引を受けられたり、基本料金をほとんど支払わなくて済む。
二部料金制では、貧しい人は基本料金を払えないという問題が発生するが、
上記の僻地の医療サービスも同様なのだが、基本的には別問題である。
確かに需要の価格弾力性の違いに応じで価格差別すべきだが、所得格差から生じる問題に対して、
いちいち所得や資産を調べたりして(僻地ならできるかもしれないが)、
政府が個々の財ごとに価格規制で対応するよりも、所得再分配という対処策が個別にちゃんとある。
まずは所得再分配政策をきっちりとやる方が望ましい。
こういう考え方を「政策割当」の問題と言い、
ティンバーゲンの定理=複数の独立した政策目標を達成するためには、同じ数の政策が必要。
マンデルの定理=政策の諸手段は、それぞれが最も効果を発揮する政策目標に対して割り当てられるべきである。
などが有名。
価格規制という政策ひとつで、不平等の是正も同時に目標とするのは間違っており、
所得分配の平等化には所得再分配という適切な政策がちゃんとあるということ。
映画館やレストランでの学割やレディースデーなどのように、価格差別のために客を識別するのが簡単で、
再販不可能な財で、企業が勝手に価格差別を行うことに関しては、もちろん自由。
そのような価格差別が次の第3種。
・ 第3種価格差別
消費者1人1人については留保価格が識別できなくても、グループ(市場別)でなら識別可能な場合、
それぞれの市場の価格弾力性の違いに応じて価格差別を行うのが第3種。
大人と子供とか、社会人と学生、男女など。
時間は無いけど金はある社会人は、需要の価格弾力性が低く、多少値段を上げても需要は減らない。
一方、価格に敏感な層は、需要の価格弾力性が高いので、値段を下げることでかえって企業の収入が増える。
「ヴァリアンの入ミク(9版)の26章4節、p422~p423」より、
価格弾力性が大きい方の市場1の逆需要関数:P1
価格弾力性が小さい方の市場2の逆需要関数:P2
それぞれの市場に、独占企業が供給するので、費用関数は、
C(Y1+Y2)
独占企業が直面する利潤最大化問題は、
P1・Y1+P2・Y2+C(Y1+Y2)
完全競争下での利潤最大化条件はP=MCだが、独占市場ではMR=MCなので、
MR1=MC(Y1+Y2)
MR2=MC(Y1+Y2)
限界費用は等しいので、限界収入も各市場で等しくなければならない。
限界収入MRは、総収入関数TR=P・Yを、需要量yで微分すると求まるので、積の微分を用いると、
∂TR dP Y
────=MR=P+P'Y=P(1+───・──) ・・・1
∂Y dY P
需要の価格弾力性をεとすると、
dy P dY P
ε=───・── → │ε│=-───・──
dP Y dP Y
従って1式は、
1
MR=P(1-───) ・・・2
│ε│
よって各市場の利潤最大化条件は、
1
P1(1-────)=MC(Y1+Y2)
│ε1│
1
P2(1-────)=MC(Y1+Y2)
│ε2│
市場1の方が価格弾力性が大きい場合、
1 1
1-────>1-──── → │ε1│>│ε2│
│ε1│ │ε2│
MC(Y1+Y2)は各市場で共通なので、
P1<P2
となる。すなわち、価格弾力性の大きい市場1では低価格、価格弾力性の小さい市場2では高価格となる。
・ ラーナーの独占度
2式と、独占市場での利潤最大化条件のMR=MCより、
1 1
MC=P(1-───) → P=MC・[────────] ・・・2F
│ε│ 1-(1/│ε│)
1
[────────]=マークアップ率(限界費用にどれくらい上乗せして価格を釣り上げているか)
1-(1/│ε│)
2F式を変形すると、
1 P-MC 1
MC=P(1-───) → P-MC=P/│ε│ → ─────=─── ・・・2G
│ε│ P │ε│
独占価格と限界費用との乖離率は、需要の価格弾力性の逆数に等しく、ラーナーの独占度という。
文献によっては、マークアップ率=ラーナーの独占度と表現しているものもある。
・ 固定費用と内部相互補助
第3種価格差別において、│ε1│>│ε2│だとすると、固定費用次第では、
価格弾力性が小さくて高価格を付けられる市場2だけに財が供給されて、
価格弾力性が大きくて低価格しかつけられない市場1には供給されない可能性もある。
しかし、ユニバーサルサービスの供給を義務付けた場合、さらに場合分けが考えられ、
ケースA:市場1への供給義務+価格差別はOK
ケースB: 〃 +価格差別も禁止
数値例次第では、ケースAは企業の参入が可能でも、ケースBは不可能な場合がある。
例えばケースAは、価格差別したところで、市場1では相変わらず利潤は負のままだが、
市場1+市場2=市場全体では、市場2だけ供給した場合よりは利潤は減るが、利潤は正となる可能性がある。
ところが、同じ需要条件(市場条件)と固定費用の下で、ケースBでは価格差別もできないので、
市場1+市場2=市場全体でも利潤が負となる可能性がある。
また、両方のケースで参入できたとしても、元々、固定費用のせいで、市場2では正の利潤、市場1では負の利潤
だったので、ユニバーサルサービスを義務付けている時点で、市場2の利潤によって、市場1の赤字を補っている
ことになり、内部相互補助という。
○ P203~P205、ティブーの足による投票モデルと地価。
1つ上の林公共の所で説明した、資本化仮説の話に該当。
アメリカのように地方交付金による地方間の所得移転が少ない国では、
地方公共財が良質で多量の地域の地方税は高くなり、その逆は低くなる。
従って、地方公共財が地価に与える影響は小さい。
P202にもあるように、地方公共財の理論(やティブーのモデル)は、
各地方自治体の人口が多く、かつ、地理的に遠く離れて、分散して点在していて、
相互依存関係の少ない(スピルオーバーの問題がない)、アメリカのような環境で生まれたことにも理由がある。
逆に日本のような地方交付金や補助金による所得移転が多い国では、
地域ごとの居住者に課せられる地方税そのものについては格差は小さい。
その分、地方公共財の影響は地価に反映される。
地主達の間では、良い公共財(公園など)は誘致合戦となり、悪い公共財(ゴミ処理場)などは敬遠される。
一方、借地・借家・借マンションなどの借り手は、公共財の影響は地価や賃貸料に反映されるので、
自分の選好に見合った地域に移動して、足による投票を行いやすい。
結局、地方交付金などによる所得格差の是正は、その名目とは裏腹に、
地価の上昇によって富裕層である地主達に吸収される。
○ P213~P216、クラブ財(地方公共財)の最適規模と不安定性
ティブーの足による投票仮説(地方公共財の市場均衡的解決)が成り立つためには、
各規模のクラブ財に対して、それぞれ需要する人数が十分大きくなければならない。
多種多様な規模のクラブ財が並存できることによって、競争が働き、市場均衡は達成される。
大都市のテニスクラブや劇場などがその例にあたる。
問題となるのは、
最適クラブ員数(N*)>総需要者数(N) ・・・1
その場合、平均費用逓減産業と同様になり、全員を同一のクラブに参加させるのが望ましい。
平均費用が逓減している区域では、限界費用はそれより小さいので収支が合わず、操業停止せざるを得ない。
強制的な費用徴収による非市場的な解決が必要となる。
もし1式とは逆に、N*<Nとなっていても、N*がNの1/2以上あるような場合、
この社会は2つのクラブを支えるには人口が少なすぎ、1つでは多すぎることになる。
N*がNの整数倍でないときは、クラブ財の自発的供給は不安定となる。

1人当たり費用(平均費用)が最小となる最適クラブ員数は、N*となる。
仮に、総需要者数N>N*だったとしよう。しかし、N/2<N*となっている。
もし2つのクラブを作って半数ずつに別れた場合、1人当たり費用=会費は、OBからOEへと下がる。
しかし、限界費用OFは、平均費用OEより小さい。
このとき、各クラブにとっては、1人追加することによる限界費用は平均費用より小さいので、
1人追加することでかえって1人当たり平均費用を減らすことができる。
引き抜かれた側にとっては、MC曲線はずっと右上がりなので、かえって限界費用が下がる。
そこで引き抜いた側が提示した条件より、さらに有利な条件で引き戻しを図るだろう。
全員が引き抜きの対象である以上、誰も「限界費用以上の会費」を支払わなくなるが、
それだと平均費用に満たないので収支は均衡せず、クラブ財の自発的供給は不可能となる。
大都市だと複数の球場が安定的に並存するのに対し、小都市では球場数が1つだと高利益なので、
2つ目を作ると両球場とも採算が取れなくなって、球場数が1になったり2になったりを繰り返すのに似ている。
数式、グラフ、数値例を用いた、もっと詳しい分析を学びたい場合は、本書を読もう。
最後に、P200~P203に戻ろう。ティブーの足による投票仮説が成立するための条件について。
1:所得獲得のための地域制約がない
2:地方自治体ごとに異なる地方公共財メニューについての完全情報
3:多種多様なメニュー(地方公共財のミックスパターン)があり、かつ、同質なメニューの供給も多数存在
4:1人当たり平均費用が最低となる最適人口規模の存在
5:便益がスピルイン・スピルアウトしない
6:地域間移動にコストが掛からない(法的・経済的)
7:地方公共財について同一の選好を持つ消費者も多数。
結局、完全競争市場的な条件が必要となる。
1についてティブー自身は、利子・配当所得、年金だけで生活する消費者を仮定。
3は種類(各財ごとの市場)そのものが多数で、1種類ごとの市場においても供給独占なし、
5は外部性(スピルオーバー)なし、6は取引費用なし、7は需要独占なし。
4については、最適サイズが無い場合、あるいは最適サイズが極端に大きい場合、
非競合財となって全員消費が望ましいことになる。
後者だと、平均費用逓減財を意味するので、地方公共財に規模の経済が働いていることを意味する。
前者だと、上記のクラブ財の最適規模で学んだように、地方公共団体間で居住者を奪い合ったり、
公共財供給が国になったり地方になったりと不安定になる。
○ 6章の所得分配
P231~P233の、現金給付vs現物給付。
西村の入ミク(黄緑色の第2版)では、4章4節、無差別曲線の応用、
岩菊と飯田のゼミナール経済政策入門の3部、P369~P372、のそれぞれに同じ内容の説明がある。
○ 7章の公共選択
複数の選択肢に対して、任意の2つを1つのペアとして多数決投票を行い、
勝者同士でまたペアを作り、同じ多数決で勝者を決めていくトーナメント方式の投票方法を、
単純多数決ルールといい、(コンドルセの)投票のパラドックスが起きる。
また、選択肢が奇数(A,B,C)で、まずAとBの多数決を行い、勝った方とCの多数決を行う場合、
後出しのCがかなり立場的に強くなる。
人々は自分の選好に従って純粋に投票しているつもりでも、提案順序を議会や官僚に操作されている可能性がある。
そもそも、上記のような投票方法は、序数的選好を示すだけで、基数的選好を示すことができない。
パラドックスが起きないような投票方法として、順位投票制、点数投票制(ボルダ投票)などがある。
前者は順位を付けた後、選択肢ごとに順位を合計する。後者は最初に同じ持ち点が各自に与えられて投票する。
ペアごとではないので、選好の強度を反映しやすく、最終的に集団全体の選好もかなり正確に表現する。
ただし、票の取引(ログローリング)という戦略的行動を防ぐことはできない。
P269の注釈より、ログローリングはアメリカの政治ジャーナリズムの用語で、
開拓時代に協力して木材を転がして運び出したことから来ているが、
文芸家達が作品の売り上げを伸ばすために、互いの作品を褒め合うことを指す場合もあるとのことw
一見、政策が違う政党同士が連立を組むのもそれが理由。
ブキャナンとタロックは、取引というのは資源配分上も、厚生配分上も望ましいので
ログローリングも望ましいと論じたが、常に社会厚生上望ましいとは限らない。
取引はその当事者双方に利益をもたらすことは間違いないが、
その決定自体は全ての人に影響を及ぼすので、取引に参加していない第三者にも外部効果を及ぼす。
その数値例がP270~P271の表7-D。
取引が無かった場合より、取引した場合の方が、社会全体で利益が減っている。
この数値例も見事なので、興味ある人は図書館とかで見つけて読んでみよう。
暗黙のログローリングというのもある。投票する人々はログローリングしていないつもりでも、
提案された選択肢が、複数の政策案の抱き合わせ(A,B,C)になっている場合、
BとCはそれほど好きじゃないが、Aを強く選好しているため、仕方なく一括案に投票するという話を、
現実でもよく耳にするだろう。大体において、人質に取られるAは、景気、雇用、所得である。
そして、どの政策案を一括にするのかも、議会や官僚が操作する権限を握っている。
7章4節、P274~P278、直接投票と間接投票についてのパラドックス、
7章5節、P285~P290、最小勝利提携、
について、ちょっと数値例の話が長いので、 雑記ノートで。
・ 「J.R.マークセン W.H.ケンプファー K.E.マスカス 国際貿易―理論と実証〈下〉 多賀出版 2000/09」
の19章、P389~P409、貿易政策の政治経済的分析。
柴田公共のP278~P281、有権者の行動(取引費用、合理的無知、囚人のジレンマ)と同内容で、
こちらのマークセン=ケンプファーの教科書で説明しよう。
19.2節、P391~。基本となる中位投票者モデル。
ストルパー=サミュエルソンの定理から、労働集約的な輸入財の国内価格を引き上げる関税は、
どのセクターに関係なく、労働の実質賃金を引き上げ、資本の実質レンタル価格を引き下げる。
人口全体を1として横軸に取り、縦軸に利益を取る。中位投票者は分布のちょうど0.5に位置する。
さて、この関税政策によって、60%の人が損失を被るとし、1人当たり損失をL、
利益を得られる残りの40%の、1人当たり利益をGとしよう。

GとLは、横軸を挟んで上下に対称とする。すなわち、G=Lとする。
原点から0.6の所までは損失グループを並べて、0.6の所から不連続となる。
0.5に位置する中位投票者は損失Lを被るのだから、関税法案は否決されるだろう。
19.3節、P393~。前節では、G=Lであった。そこで設定を変えてみよう。対象は貿易自由化政策とし、
G’>L’ かつ 0.4G’>0.6L’としてみる。

0.6×L’=長方形Aの面積で、グループL’の総損失。
0.4×G’=長方形Bの面積で、グループG’の総利益。
貿易自由化法案によって、社会全体が得られる純利益は正(A<B)である。
しかし、中位投票者の定理により、法案は否決されてしまうのである。
パレート効率性の基準で言えば、損失を受ける人がいる限り、そのような政策はパレート効率的ではない。
しかし、その基準だけだと採用できる政策が限定的になる。
そこでカルドアの仮説的補償原理によれば、利益を受けた人が損失を受けた人に補償して、
それでもなお利益が確保できる場合には、たとえその補償が実際には行われなかったとしても是認される。
このような補償は、票の買収に等しく、ログローリング(票の取引)に等しい。
しかし、すぐ上で述べたように、ログローリングが常に望ましいとは限らない。
アメリカで1930年に、スムート=ホーリー法(Smoot-Hawley)が、
ログローリングによる厚生低下の教科書的な事例としてかなり有名。
各産業の支援を受ける議員同士が、他のセクターの関税にも賛成し合った結果、
平均保護関税が輸入額の50%以上にまで上昇したという。
中位投票者定理が成り立つためには、自分の利得に関して完全に知っていること、
そして忠実に自分の選好に従って投票することを仮定する。
しかし利得を理解するためには、費用をかけて情報収集しなければならない。
さらに投票所に行って投票すること自体にも、時間や労力などの費用が掛かる。
これらの費用は、政治参加による利益と比較されなければならない。
自分の一票が選挙結果を左右する可能性はゼロに近い。
個人の投票という行動から得られる期待利得(確率を考慮した利得)はかなり小さく、
一方で投票にかかる費用を考えると、無知なまま棄権しておいた方が合理的かもしれない。
P398~。関税によって特定の産業を保護するケースで、今度は、利益を受けるグループはたったの5%、
損失を被るグループは大多数の95%としよう。
しかし、1人当たり利益のGは非常に大きく、一方で1人当たり損失のLは非常に小さいとしよう。
(コメの輸入規制で、米の値段が少々上がったところで、1人当たり損失は微々たるものだったり。)
G>>>>>L

それでも社会全体では、0.95L>0.05Gとする。ネットで社会厚生は低下(A>B)する。
このような場合、利益を受ける小グループは、組織的な投票行動(お互い監視し合ったり)の費用に比べて、
利益の方が大きいので、積極的に活動できる。さらに重要なのが、そういう活動にあたっての資金面である。
このような活動費は、投票後に得られる利益から提供される可能性すらある。
このような活動を、レントシーキングという。
レントとは超過利潤のことであり、大抵の場合、参入規制や保護政策によって作られる独占利潤である。
19章4節、P400~。不確実性のもとでの中位投票者モデル。
貿易自由化政策の話に戻ろう。60%の人が+Pの利得を得るグループB、
40%の人が-Pの利得(つまり損失)を得るグループAとしよう。
社会全体の純利益は、0.6P-0.4P=0.2Pなので、貿易自由化政策は実施されるべきである。
一方、輸出セクターで用いられている生産要素は40%とし(Bに属している)、
その40%の人達は貿易自由化後の厚生増加について正確な情報を持っているとする。
残りの60%のうち、1/3(20%)の人達も+P(Bに属している)、
2/3(40%)の人達が-P(Aに属している)となるのだが、
この残りの60%の人達は、厚生が高まるのか、それとも低下するのか不確実だとしよう。
すると、この残りの60%の人達の期待利得は、1/3P-2/3P=-1/3Pとなる。
つまり、自分がAなのか・Bなのか、利得を得るのか・損失を被るのか、情報を持っていないが故に、
確率的に期待利得はマイナスと考えてしまい、全員が反対票を投じることになる。
従って、中位投票者モデルの下で、貿易自由化法案は否決されてしまう。
例えば世界の生産能力が向上し、国内の農業の生産費用が相対的に高くなったとしよう。
関税や輸入数量割当などの政策が採られなければ、農業に従事する生産要素の所得を脅かすだろう。
このとき、貿易自由化政策は一国全体の厚生を高めるとしても、
直接に農業とは関わりのないセクターの生産要素であっても、その効果は不確実なのである。
自身が同じ立場に立たされた場合に保護を受けるための暗黙の保険として、
産業保護政策を支持することは十分にありえる。
「現状維持への偏り(status quo bias)」と呼ばれ、
このタイプの保護主義は、「保守主義的社会的厚生関数」と呼ばれるもので説明される。
つまり、とにかく現行のセクター別の所得分布を一定に維持するのが目的となる。
○ 次の板谷公共の15章4節、P373~P377、ニスカネンの(官僚の)予算最大化モデル。
柴田公共では、P281~P285で同内容。
板谷公共の記述の方を中心に書くが、同じ話題が続いた方がまとまるのでこちらに書く。
売上高最大化仮説の政府版モデルである。
そもそも公共財の供給は、政府による供給独占となっている(対民間に対して)。
また、立法や行政の実務を担当する行政府(各省庁の官僚)は、
公共財供給に関する生産関数や費用関数などの技術情報に関して、
立法府(政治家)よりも詳しいという意味で、情報の非対称性が存在している(対議会に対して)。
さらに、情報の非対称性だけではなく、官僚が作成した予算案を、承諾するか・しないかを迫るように、
議会に提出することが制度的に認められている。
これがまた結構重要で、情報を握っているだけではなく、議会に対してかなり強い交渉力を持つ。
(一般的にAさんとBさんで考えるとわかりやすいだろう。はいといいえしか選択肢の無いAさんはつらい。
細かいメニューを注文できないし、いいえと言っちゃうと、最大で利得は0なので、飲まざるを得ない。)
予算を含めた立法作業について、政治家と官僚の間には、プリンシパル-エージェント関係がある。
しかし、情報の非対称性があると、依頼者(プリンシパル)の利益よりも、
代理人(エージェント)自身の利益を追求するようになる。
これをエージェンシー問題といい、それによって発生するプリンシパルにとっての不利益や非効率、
あるいはモニタリングコストも含めたコストを、エージェンシーコストという。
官僚にとっての自己利益(効用関数)とは、金銭的収入や雇用の安定だけではなく、
名声・評判・名誉・地位、社会的貢献、忠誠心、プロ意識などの、非貨幣的所得も含まれる。
そして、これら多くの目的を達成する上で、何より必要となってくるのが、
自らが所属する組織の維持・拡大=予算の獲得である。
とにかく予算を獲得し、組織を拡大できれば、上記の目的から得られる効用は全て増加するからだ。
そこで、公共財から得られる便益の関数をB(G)としよう。
国民にとっての留保価格(支払意思額)なので、B(G)=予算と言える(便益分だけ税金を払ってくれる)。

限界便益は逓減(B'(G)>0だが、B''(G)<0)、
限界費用は逓増(C'(G)>0であり、C''(G)>0)。
公共財供給の効率的水準は、限界便益=限界費用(B'(G)=C'(G))となる、E点およびG*点である。
しかし、官僚にとっての効用最大化水準となる公共財供給量は、F点およびG+点となる。
官僚の効用最大化問題を解いてみよう。まず、官僚にとっての制約条件は、B(G)≧C(G)である。
情報の非対称性より、議会は費用関数C(G)の形状を知らないので、
費用C(G)が予算B(G)をオーバーしない限り、その予算案は通るからである。
一方、予算であるB(G)が、まさに官僚にとっての目的関数となる。ラグランジュ関数は、
L=B(G)+λ[B(G)-C(G)]
最適化の1階の条件は、∂L/∂G=0と、∂L/∂λ=0なので、
λ
B'(G)=────C'(G) および B(G)=C(G)
1+λ
B(G)=C(G)となる点は、原点とF点があるが、λ>0なので、B'(G)<C'(G)となる。
(制約条件のB(G)≧C(G)は、不等式制約なので、厳密にはクーン=タッカー条件となる。
相補性条件より、B(G)-C(G)=0ならば、λ>0である。)
従って、F点およびG+点が、効用最大化(予算最大化)の水準となる。
上記のラグランジュ関数を見てもわかると思うが、柴田公共のP284より、
官僚が一般人と異なる行動原理となるのは、官僚だけが特殊な効用関数をしているからではない。
官僚が一般人と比べて非倫理的なのではなく、一般家計とは異なる制約条件に直面しているからである。
一般人の誰しもが、同じ制約条件に直面すれば、同じ行動を取る。
効用関数に非貨幣的所得が含まれているかもしれないが、官僚だけではなく民間にもある。
従って、官僚の非効率を正すには、効用関数の方ではなく(心を入れ替えろと道徳心に問い掛けるのではなく)、
直面している制約条件、すなわちシステム(制度)そのものを変える必要がある。
上記のエージェンシー問題も、情報の非対称性の解消とインセンティブ設計が必要となる。
情報公開、モニタリングやチェック、責任と罰則。(エージェンシー問題の詳細は、組織の経済学を参照。)
● 「板谷淳一 佐野博之 コア・テキスト公共経済学 新世社 2013/01」
○ 9章、コモンズの悲劇(共有地の悲劇)。柴田公共のP87~P94も混ぜて一緒に説明する。
山・海・河川・大気などは再生可能資源(非枯渇性資源)と言われ、一定の浄化能力や再生産能力がある。
その一定の範囲内であれば、採取したり利用しても資源全体として減らないという意味で、
その共有地(の資源)はストックとして考えられる。
ところが、その一定の能力を超えるような汚染や乱獲があると、ストックそのものが減少する。
所有権が確定しておらず、共有地(コモンズ)となっている資源に対して、
オープン・アクセス(自由参入)になっていると、過剰利用や過剰採取が起きる。
自分がストックを維持しようとして今日の収穫を手控えても、明日は他の人に収穫されてしまう。
囚人のジレンマになってしまいそうなことが、この段階ですでにわかる。
自分の収穫や利用が、相手の収穫や利用を減らすという意味で外部性があり、混雑現象とも言える。
1:ストック(共有地)は大きいほど収穫・利用しやすい。Nを利用者数、Sをストックとすると、
Y=F(N,S) ∂F/∂N<0 ∂F/∂S>0
Yは1人当たり収穫量を表し、右辺のFは収穫関数という。
ストックが小さくなるほど同じ収穫量にかかる費用は大きくなるので、∂F/∂S>0となる。
混雑費用(∂F/∂N<0の影響)も、収穫関数の方で表す。
Nの効果やSの効果とは別に、1人当たりの生産活動にかかる費用をwとする。
生産物の価格をPとすると、本来ならP=MCが利潤最大化条件なのだが、上記の設定の下での最適化問題は、
利潤関数:NPF(N,S)-wN=[PF(N,S)-w]N
をNで微分して0と置かなければならない。
∂F(N,S)
PF(N,S)+NP──────=w ・・・9.1
∂N
ちゃんと収穫関数の中のNまで考慮して、最適な利用者数Nを求めているということは、
利用者全員で1つの会社を作って、利用者数を制限(コントロール)しながら共同利潤を考えているに等しい。
∂F/∂N<0より、9.1式の左辺の2項目は負となり、
Nが大きくなることによる収益の低下をちゃんと反映している。
一方、共同利潤を考えずに、オープンアクセスによって個人個人が自分だけの利益を考えて生産すると、
PF(N,S)-w>0である限り参入してしまう。仮定により、∂F/∂N<0なので、最終的に均衡では
PF(N,S)=w
となるまで参入が続くだろう。この条件は利潤関数をNで割っただけであり、
平均生産物価値=平均費用
9.1式の利潤最大化条件を考えると、2項目が無視されており、過剰収穫になっていることは明らかである。
この1の説明は、共有地の利用者数が多いケースで、少ないケース(例えば2人)だと
囚人のジレンマのように非協力ゲームで説明されることが多い。相手の戦略を与件として、自分の最適戦略を求める。
市場需要全体に対して、相手の生産量を所与として、自分の利潤を最大化するような最適反応戦略と来れば、
クールノーモデルであり、実は共有地の悲劇と数式的には同じ構造となる。
板谷公共の9章の3節にその説明があり、他の教科書だと
「中山幹夫 はじめてのゲーム理論 有斐閣 1997/09」の3章3節にもある。 ゲーム理論ノートにも引用した。
ただし、板谷公共のP218によると、数値例次第では囚人のジレンマにならず、
パレート効率的な利得が実現する場合もあるとのこと(P219の表9.2)。
オープンアクセスで参入が容易だからこそ悲劇が起きるのだから、
上記の記号で言えばwが大きくてそもそも参入できず、結果的にパレート効率的な収穫量と同じになる可能性もある。
2:ストック外部性。柴田公共のP87~P94。
1の収穫関数から求まる収穫量が、今期のSに対応したストックの成長量以下なら、Sは減らない。
1の定式化で、NとSはそれぞれ独立のように見えるが、実はNが増加すれば来期のSは小さくなる。
このような外部不経済を、ストック外部性という。
逆に言えば、1の問題はNで偏微分して最適人数を考察しているが、そのNの変動にあわせてSは変化しない。
考慮されているのは、9.1式の2項目の「混雑費用によるフローの減少」だけである。
より詳しく見ていこう。再生可能資源は、生産能力のある資本ストックのように、
資源そのものを自ら新たに生産し(フロー)、そのフローが新たに追加されることで、ストックそのものも増やす。
資源(ストック)の成長率が10%ならば、そのフロー部分を消費しても、ストック全体は減らない。
同じ量のストックを毎年残せるので、永久にその10%分のフローを消費し続けることができる。
もし、10%以上に乱獲して、過剰利用・過剰採取してしまうと、ストックそのものを減らしてしまう。
ただし、フロー部分を消費しなければ、無限に成長し続けるかというと、そうでもない。
フローの量は、ストックの量に依存し、魚で言えば、生息数が多くなるにつれて、
ストックの成長率も大きくなっていく(ストックの絶対値だけが大きくなるのではなく、その成長率も大きくなる)。
ところが、生息数が多くなり過ぎると、エサ不足(混雑減少)となって成長率は下がり始め、
いつか成長率は0となってストップする。
一方、生息数が少なくなると、子孫を残すためのパートナーを探すのが難しくなり、
出生率が下がり、たとえストックが増加したとしても、成長率は低くなる。
(ストックの絶対値が小さくなるだけではなく、その成長率も小さくなる。)
最悪の場合、ストックが小さくなりすぎて、自然回復(自然再生)できなくなり、
成長率がマイナスとなって、絶滅の道を回避できなくなる可能性もある。

横軸=ストック量(St)
縦軸=ストックが生み出す増加量(フロー量)=⊿St=St+1-St
フロー=St+1-Stというのは、どういう意味なのかというと、
例えばC点では、今期のフローがプラスなので、今期のストックに追加されて、来期のストックそのものが増える。
すなわち、t+1期には、ストックはC点より右側に来ている(例えばD点)。
ストックがある値に決まったら、それ以後ずっとその値を取り続けるわけではなく、
成長曲線で決まるフロー量に従って、横軸上の点は動き続けるのである。
そういう意味で、図2-10の成長曲線は、動学方程式ともいう。
さてC点を越えると、横軸のストックが増加するにつれて、混雑減少(エサ不足)によって、
縦軸のフローは(プラスではあるが)減少していく。B点になると、飽和状態でそれ以上増えない。
横軸=縦軸の値が0の線 → ⊿St(フロー)=0
成長曲線と、横軸との交点では、もはやストックは不変となる。
そのような状態を定常状態と呼び、交点を定常均衡点(単に均衡点)という。
定常均衡点は2つある(複数均衡)。A点とB点だが、まずはB点から見てみよう。
B点より左側では、成長曲線は縦軸の値(フロー)がプラスなので、右に動く力が働く。
一方、B点より右側では、マイナスなので左に動く力が働く。
B点から出発して、少し左右に動いてしまっても、またB点へと戻る力が働くので、B点は安定的な均衡点という。
A点は定常均衡点ではあるが、少しでもA点より左右に動いてしまうと、もはやA点には戻らない。
A点は不安定な均衡点という。たまたま最初にA点出発じゃない限り、A点には到達しないし、
不安定なので、少しでも動くと戻らない。
A点より右側にいればとりあえずストックは増えていくので心配ないが、
人為的な乱獲や環境汚染、自然環境の変化や災害によって、外生的な変化や圧力が大きく加わることで
A点より左側に行ってしまうと、絶滅への道を辿ることになる。
A点は、種が絶滅するかどうかの臨界点(分水嶺)とも言える。

図2-11は、図2-10の成長曲線を、別表現したものであり、動学方程式と呼ぶことにする。
例えば、⊿St=aSt+b → St+1-St=aSt+b → St+1=(1+a)St+bとすることで、
縦軸を⊿StからSt+1に変更しているだけで、両者は同質の方程式である。
またこのような方程式は、t期の値が決まれば、それ以降順次St+1、St+2、・・・の値が決まっていく。
ストック量Stが時間を通じてどのように動いていくのか、その動き方を記述した方程式なので、動学方程式という。
ちなみに、離散時間だと差分方程式、連続時間だと微分方程式になる。
原点を通る45度線:St+1=St(x-y平面で言えば、y=xなので傾きは1であり、その角度は45度。)
図2-10の成長曲線と、横軸との間の垂直距離(=フロー=St+1-St)が、
図2-11の動学方程式と、45度線との間の垂直距離になっている。
例えば、図2-10のCC’の距離=図2-11のCC’の距離。
今期のストック(St)が、C点だったとしよう。
動学方程式に従って、t+1期のストック量(St+1)が、縦軸上で決まる。
しかし、話はそれで終わらない。縦軸上で決まったSt+1から、右に進んで45度線とぶつかった所が(D点)、
次の期に横軸で取るSt+1の値となる。
横軸上で決まったSt+1から、さらに動学方程式に従って、St+2の値が縦軸上で決まる。
以降、期が進むごとに、動学方程式と45度線の間を、右上にジグザグに進み、最終的にB点で均衡する。
図2-10に戻ろう。上記はフロー部分を消費しない話だった。
フロー部分をまるまる消費すれば、均衡点(AやB)以外でも、ストック量は不変となる。
例えば、E点とF点を例に取ろう。両点は同じフロー量だから、どちらも是認されるかというと、そうでもない。
F点の方がストックが大きいので、同じフロー量を捕獲・採取するなら、F点の方が費用が少ない。
そういう意味で、フロー量が同じというだけでは無差別とは言えず、E点は低位均衡、F点は高位均衡という。
そこで、ストック外部性も含めた共有地の悲劇の解決策として、
1:個人や1つの会社、1国が所有する。あるいは共同管理。
共有地の悲劇と来れば、オープンアクセスを防ぐための所有権の確定や、
あるいは組合による共同管理で生産や収穫をコントロールという話がセットになることが多い。
所有権の設定のケースは、小規模な共有地で、山林などではよくある話。
逆に海などは規模が大きすぎて費用が掛かりすぎるので、共同管理となることが多い。
2:ピグー税
9.1式で言えば、オープンアクセスによって無視されていた2項目を、ピグー税として課せば、
外部性は内部化されてパレート効率的になる。
しかし、共有地が多国間にまたがる場合は、統一政府が無いと難しい。
小規模で、混雑してきた時のピークロードプライシングなどは有効。
3:数量規制や禁猟(禁漁)期間の設定
柴田公共によると、禁止期間設定の場合は、解禁期間で相変わらず乱獲が起き、
短期的に大量収穫・生産するための大規模投資した設備が、禁止期間では遊休しているとのこと。
4:利用権(許可証)の売買市場
ピグー税は、限界外部費用曲線、市場供給曲線(産業全体の私的限界費用曲線)と市場需要曲線、
の3つの情報を政府が知っておかなければならない。限界外部費用+私的限界費用=社会的限界費用。
数量規制になると、個別企業の私的限界費用曲線の情報まで知っておかなければならない。
個別企業同士の限界利潤が等しくなるまで数量割当を行わなければならないからだ。
CO2排出権取引市場などは、排出権を与えれば(すなわち所有権を確定して内部化すれば)、
後は民間同士で勝手に取引が行われてパレート効率的になる。
その市場で決まる価格は、あたかもピグー税と同じ働きをする。
こっそり生産したり排出したりする監視費用については、ピグー税などと同じなので、その点で差異はない。
問題は、最初に排出権をどのように与えるかという配分問題。
均等配分すれば、元々排出の少ない企業が一方的に得をするし、
過去の排出実績に比例させるのも、それはそれで不公平となる。
ただし、配分が国別の場合、均等分配なら、それまで排出の少なかった発展途上国から、
排出の多い先進国が排出権を買うという形で、所得の再分配が起きるとも言える。
板谷公共ではアンチコモンズの悲劇も説明される。
発明品や医薬品の開発において、他の特許をたくさん使用しなければならない場合、
逆に所有権が細分化され過ぎて取引費用が大きくなり、開発を断念するケースも生まれる。
有用な資源の過少利用という意味で、逆の悲劇が生まれる。知的財産権の保護の問題は難しい。
○ 6章5節、P161~P162、マクガイアー・モデル
林公共のP210~P212にも同じ説明がある。
ティブー仮説はティブー自身は数式によるモデル化を行っておらず、マクガイアー(M.McGuire 1974)が、
クラブ財の最適供給モデルを若干修正することで説明。
地方公共財は1種類で、住民の選考は同一(異なる場合へ拡張すると、移動しあって最終的には同一同士となる)、
利用回数も固定(メンバー数をn、利用回数vとして、vを可変に拡張すると、
最適となるn×vを一定に保った状態で、vを増やせば、その分最適メンバー数nが減るだけ。)。
効用関数:U(x,G) ・・・1
予算制約:x+C(G,n)/n=I ・・・2
C(・)は費用関数。ちなみに同書の6.1節では、クラブ財の最適化条件を求めているが、
そことの定式化の違いは、混雑現象を表すnが、1式の効用関数に変数として入っている代わりに、
2式の中の費用関数にはnが入っていない。
混雑を効用の減少として表すか、混雑費用の増加として捉えるかの違い。
林公共の方では、消費者(住民)の予算制約:y=x+p(yは板谷で言えば2式のI、pはクラブ財の会費)。
クラブ財の収支均衡条件は、pn=C(G,n)。
さて、2式を1式に代入して、最適化する(微分してゼロと置く)。
U(x,G)=U(I-C(G,n)/n,G)
まずGについて微分してゼロと置くと、
∂U ∂C(G,n)/n ∂U ∂U/∂G ∂C
───[-────────]+───=0 → n──────=─── ・・・6.7
∂x ∂G ∂G ∂U/∂x ∂G
次にnについて微分してゼロと置くと、
∂U (∂C/∂n)n-C ∂C C
───[-─────────]=0 → ───=── ・・・6.8
∂x n^2 ∂n n
6.7式はサミュエルソン条件。限界代替率をn倍にしてるということは、
限界代替率を住民数(クラブ会員数)で合計しているに等しい。右辺は地方公共財(クラブ財)の限界費用。
一方、pn=C(G,n)をnで微分すると、p=∂C/∂n。
費用関数Cの中のnは、混雑費用を表わすのだから、クラブ会費pは、限界的な混雑費用と等しければ最適。
6.8式は最適人口規模を表す。限界費用曲線は平均費用曲線の最低点を下から上へと突き抜けるので、
限界費用=平均費用となるのは、平均費用が最小となる点である。
柴田公共の5章のP207~P212では、6.8式を図解だけで導出し、
(∂C/C)/(∂n/n)=1(弾力性が1)と表現している。
林公共(P212)によると、平成の市町村合併も同理論から説明でき、
人口規模を確保して平均費用を最小化することで、住民の効用を最大化。
この理論をベースに、公共財供給の費用関数を推定して最適人口規模を求めると、
平均費用を最小にする地域人口は20万~40万とする研究が多いそうだ。
ただし、麻生良文先生のサイトによると、http://fs1.law.keio.ac.jp/~aso/guide.html
「最近では,市町村合併に関して誤った議論が横行しています。
よくある議論は,市町村の最適人口規模を実際のデータによって求めると
人口規模が15万とか20万くらいのところで住民一人あたりの歳出規模が最低になる。
だから,行政事務の効率化のために,市町村合併を推進すべきだという議論です。
ちょっと考えてみればわかりますが,最適な規模は,地方政府の供給するサービスの便益が
どの地理的範囲まで及ぶのかに大きく依存します。
人口密度の高い地域と低い地域がありますから,それらを一緒にして議論することはナンセンスです。
また,現行の制度のもとで費用が最小になるような人口や面積の規模があったとしても,
それは現在の中央と地方政府の役割分担や,政府がどの程度私的財を供給するのかに依存します。」
地方交付税に関する説明も大事。
「地方交付税や補助金についても,あまり理論的な議論が行なわれていません(専門家の間でも)。
地方財政のほとんどの本では,「財政力の格差」を是正するために
地方政府間の財政調整制度が必要だと書いてあります。
ある地域に高所得者が多いために,税収格差が発生している場合,地域間の再分配ではなく,
個人を対象にした再分配を行うべきです。
(すなわち、所得再分配は地方ではなく国の役割。地方が担うべきなのは準公共財である地方公共財。)
地域を対象として再分配を行うと,豊かな地域の低所得者から
貧しい地域の高所得者に再分配が行われるかもしれません。」
○ 10章、租税競争(水平的財政外部性と垂直的財政外部性)。
・ 10章3節、P236~P239、まずは水平的財政外部性について。
租税競争の参加者が少数(例えばプレイヤー数2で、地域1と地域2)の場合、
相手の税率を与件として、こちらの税率を決めるという意味で、非協力ゲーム的な構造となる。
資本は移動できるが、労働者は移動できないと仮定。
人口規模が同じで、L1=L2=1と基準化(後でこの設定を変更してみる)。
各地域に企業は1つだけとし、地域1と2の企業の生産関数は1次同次で、同一とする。
Y1=F(K1,1) Y2=F(K2,1)
このように設定するのは、地方間の税率の違いによる資本移動の効果だけを分析したいためで、
その他の条件を一定としたり、簡略化したり、等しくしている。
さて、一般的な分析では、利潤最大化条件から資本の最適量を決める(資本需要関数を求める)。
機会費用としての利子率と、資本の限界生産力が等しくなるように、裁定条件が成り立つ(どちらで運用しても一緒)。
しかしここでも、資本移動の効果だけを分析したいので、資本の総供給量は固定とする。
_ _
資本市場の需給均衡条件式:K1+K2=K (教科書では、K=2と基準化)
需給量は変化しないが、じゃあ何の価格差に応じて、どんな裁定行動を取るのかというと、
地方政府間の税率の違いに応じて、資本の移動によって裁定取引を行う。
∂F(K1,1) ∂F(K2,1)
裁定条件式:───────-t1=──────-t2
∂K1 ∂K2
(∂Fi/∂Ki)-ti=税引き後の(限界)資本収益率 i=1、2
地域1の企業(以下、企業1)の資本需要関数を求めると、
裁定条件式は、本来なら右辺は市場利子率rになるが、上記のような設定となる。
_
そして、資本の需給均衡条件式から、K2=K-K1を代入することで、
K2の部分を消して、K1だけの式にして、K1=右辺(t1とt2のみの関数)となる。
(なぜなら、労働量は1で基準化してるので、生産関数の変数はKのみだから。)
基本的には、K1はt1の減少関数で、t2の増加関数となる。
- +
企業1の資本需要関数:K1=t1とt2のみの関数=K1(t1,t2)
_
企業2の資本需要関数を求める時は、裁定条件式に、K1=K-K2を代入して、K1を消せばいい。
すると、生産関数が同一であることから、
+ -
企業2の資本需要関数:K2=K2(t1,t2)
また、資本需要関数とは言っているが、資本の総供給量は固定されいているので、
結局は資本を移動させる行動原理(インセンティブ)を意味する。
さて次に、地方政府はどのように税率を決めているのか(どんなインセンティブがあるのか)、
家計の効用最大化、企業の利潤最大化のように、地方政府はどんな最適化行動を行っているのか。
まずt1やt2は資本に対する税率なので、その税収を移動しない労働者に移転所得として再分配を行うとする。
そして地域住民である労働者の所得を最大化するように税率を決める。
しかしここでトレードオフというかジレンマが生じる。税率を上げすぎると企業(資本)に出ていかれてしまう。
予算や費用関数などの制約条件の下で、最適化を行わなければいけないように、無限に税率を上げることはできない。
このような労働者の所得最大化問題を解くために、まずは目的関数である労働者の所得は、
∂F(Ki,1)
Ii=F(Ki,1)-───────・Ki+tiKi ・・・10.3
∂Ki
1次同次の生産関数とオイラーの定理(完全分配定理)より、収入(売上げ)は生産要素に分配され尽くす。
経済数学ノートの 「21:オイラーの定理」を参照。
労働所得Iiは、10.3式の1項目の生産量から、2項目の資本の所有者に支払われる資本所得を引いて、
資本への課税から得られた租税収入は、そのまま労働者への移転所得とする。
資本所得が(∂F/∂K)・Kとなっている理由は、実質資本コストをrとすると、資本所得はrKであり、
利潤最大化の下では、資本の限界生産力=実質資本コスト(∂F/∂K=r)だから。
10.3式のKiの部分に、企業iの資本需要関数を代入して、Kiを消せば、
(資本需要関数と連立している時点で、資本に移動されちゃうことを制約条件として考慮してることを意味する。
効用最大化問題を解くときに、効用関数の中に予算制約式を代入して微分して0と置くのと一緒。)
今度は労働所得Iiが、t1とt2のみの関数となる。
そしてKiを消したI1とI2も、生産関数が同一であることから、t1とt2を入れ替えただけの同じ式となる。
最終的に地域iは、t1とt2のみの関数となった10.3式を最大化したいのだから、
地方政府にとっての操作変数であるtiで偏微分して0と置く。
偏微分するということは、例えば地方政府1は、t2をいったん所与(定数)として、
t1で偏微分することを意味する。
∂Ii/∂ti=0と置くので、すでに消したKだけではなくIも消せて、
最後に残る関数は、t1とt2の方程式となる(所与とした方は変数に戻る)。
それがまさに、両地域の最適反応関数であり、地域1と2ともに、t1とt2の方程式となるので、
t1-t2平面に両方程式を描いて、交点を求めたものがナッシュ均衡となる。
最適反応関数も、生産関数の同一性から、t1とt2を入れ替えただけの同じ式となる。
y=ax+bだったなら、x=ay+bとなるような感じで、横軸をy、縦軸をxにすれば同じグラフとなる。
従って、両方程式の交点は、原点を通る45度線上に存在することになるので、
ナッシュ均衡:t1=t2=t#
ナッシュ均衡となるt#は、パレート効率的な水準と比べて過少になる(引き下げ競争)。
もし協力して同じ税率を課せば、税率をもっと上げることができ、住民の厚生(労働者の総所得)を高められる。
その上手い説明がP238にあり、同一の生産関数で、同一の税率なので、資本需要関数より、
_
K1=K2 → K1=K2=K/2 (資本市場の需給均衡条件式より)
他方で、同じ税率を課せば資本移動の心配が無いので、t1=t2を同時に上げて行けば、
各地域の税収tiKiを増やせて、両地域の住民(労働者)の厚生を高めることができる(パレート改善)。
水平的財政「外部性」と言われる所以で、もし地域1が資本税率を上げると、資本が地域2へと移動してしまい、
地域2からすると、何もしていないのに、税収が増えて、地域2の住民の厚生が高まる。
地域1が地域2に対して、正の外部効果を与えていると言っていい。
逆に地域1が資本税率を下げると、地域2から資本が移動して来るので、
地域2は何もしていないのに、地域1のせいで勝手に税収が減って、厚生が低くなる。
地域1が地域2に対して、負の外部効果を与えていると言っていい。
協調して(協力して)一緒に税率を上げれば、両地域とも厚生が高まるのに、
租税競争によって税率をパレート効率的な水準よりも下げしまう(過当競争)。
租税競争のナッシュ均衡は、まさに非協力ゲームにおける非協力解(ジレンマ)である。
・ 10章4節、P240~P242、人口規模が異なる地方政府間の租税競争。
4節では、L1=1、L2=2とする。それ以外の設定は、すべて3節と同じである。
結論だけを述べると、まず資本需要関数が異なってくる。t1=t2だった場合、K1<K2となる。
なぜなら、裁定条件を満たすためには、t1=t2である以上、資本の限界生産力が等しくならなければならない。
地域2の方が労働量が多いので、資本の限界生産力が地域1と等しくなるまで、
地域1から地域2に向かって資本が移動し続けることになる。
P242では資本需要の税弾力性(∂Ki/∂ti)・(ti/Ki)を導出しており、t1=t2だった場合、
地域1の資本需要の税弾力性>地域2の資本需要の税弾力性
となるので、人口の少ない地域1は、人口の多い地域2よりも、税率を引き下げるインセンティブを持つ。
逆に人口の多い地域2では、多少税率を上げても、地域1の方に資本が移動してくれないおかげで、
税率を高くするインセンティブがある。労働量が多いため、それでも資本が来てくれると思っているのだろう。
ヘクシャー=オリーンモデルで言えば、相対的に労働量の多い国は実質賃金が低く、資本収益率は高いからだ。
後は3節の手順と一緒で、I1とI2のそれぞれに、K1とK2の資本需要関数を代入して、K1とK2を消し、
∂Ii/∂ti=0を求めてIiも消すと、t1とt2の方程式(地域1と2の最適反応関数)が求まる。
最適反応関数同士の交点であるナッシュ均衡では、t1<t2となる。
・ 10章5節、P243~P246より、垂直的財政外部性について。
水平的財政外部性のときとは違って、地方政府と中央政府は同じ課税ベースに対して参入するので、
共有地の悲劇(つまりクールノーモデル)と同じ構造となる。
資本の記号はKだけ。人口は1に基準化、国税をtC、地方税をtLとすると、同じKに両方が資本税として課される。
資本移動の問題は関係なくなるので、本来の利潤最大化条件式より(資本の総供給量も別に一定ではない)、
∂F(K,1)
企業の資本需要関数:──────-tC-tL=r ・・・10-5-1
∂K
労働量は1で基準化してるため、生産関数の変数はKのみなので、1式は、K=tCとtLのみの関数となる。
rは、企業にとって所与となるので、企業が操作できる変数ではない。
そして、K1とK2の区別も別にないので、資本需要関数は1式の一本だけである。
地方政府と中央政府の最適化問題は、住民の所得最大化だと同じ目的関数になっちゃうので、税収最大化とする。
税収を上げると、資本需要関数より、資本が減っちゃうというジレンマとなる。
しかも、例えば地方税率が上がれば、国は何もしていないのに国税収入が減ってしまうという意味で、
負の外部効果が働く。
中央政府の目的関数:税収=tC・K
地方政府の目的関数:税収=tL・K
操作変数はそれぞれの税率なので、資本需要関数を制約条件として目的関数に代入してから、
∂tC・K ∂tL・K
─────=0 ─────=0 ・・・10-5-2
∂tC ∂tL
どちらも、tCとtLの方程式(最適反応関数)となる。tC-tL平面に両方程式を描いて、交点を求めたものが
ナッシュ均衡となるのだが、1式と2式の構造を見れば分かるように、操作変数が違うだけで、後は同一である。
従って、最適反応関数は、tCとtLが入れ替わったような式となる。その交点であるナッシュ均衡は、
tC=tL=t# ・・・10-5-3
次に、そのナッシュ均衡がパレート効率的かどうかを調べるために、
国と地方が共同で(協力して)税収の「合計」を最大化してみよう。目的関数は、
(tC+tL)K=tC・K+tL・K ・・・10-5-4
となる。4式をtCで偏微分して0と置いたものと、4式をtLで偏微分して0と置いたものは、
式の構造を見れば分かるように、どちらも同一のKとなり、
K=0
最適反応関数はまったく同じで、一本しか導出できない。
元々、一本しかない資本需要関数の右辺は、tCとtLのみの関数なので、
K=0と置くと、tC-tL平面に一本のグラフ(tCとtLの方程式)が描かれるだけとなる。
そのグラフ上では、税収の合計を最大にするtCとtLの組み合わせが、無限にある。
そこで両政府が話し合って、試しに
tC=tL=t*
と、設定してみると(一本の最適反応関数のグラフと、tC=tLという原点を通る45度線との交点)、
ナッシュ均衡の税率よりも低くなる(具体的な数値例とグラフは教科書を参照)。
3式のt#を資本需要関数に代入し、求まったKと共に税収の合計を計算してみると、
tC・K=tL・K=t#K ナッシュ均衡の税収の合計=2t#K ・・・10-5-5
一方、t*を資本需要関数に代入し、求まったKと共に4式に代入してみると、
協力した時の税収の合計=2t*K ・・・10-5-6
となり、2t*K>2t#Kが示される(具体的な数値例とグラフは教科書を参照)。
すなわち、ナッシュ均衡の税率は過大に設定されやすい。
これは各政府が競争的に自分の税率を決めるとき、負の外部性を考慮せずに決めるためで、
必ずパレート効率的水準より税率は高く、税収は低くなる。
同じ課税ベースという共有資源を奪い合う、共有地の悲劇と同じ構造である。
・ 10章6節、P246~P249、公共支出外部性(公共支出競争)。
企業誘致のための公共支出競争や補助金競争も過剰になる。
水平的財政外部性とほとんど同じ構造で、L1=L2=1に基準化。
資本市場の需給均衡条件式:K1+K2=Kバー(教科書では、Kバー=2と基準化)。
公共支出競争なので、地方政府が操作するのはG1とG2になる。
税金は住民の方に課され(水平的財政外部性のときは資本に課税)、一括税Tiとする。
地方政府の予算制約式は、Ti=Gi。
生産関数F(Ki,1,Gi)の中には、最初からGiが入っている。
裁定条件式は、企業1と2の資本の限界生産力が等しくなるまで、資本が地域間を移動し続ける。
裁定条件式と資本市場の需給均衡条件式から資本需要関数を求めると、G1とG2のみの関数となり、
K1はG1について増加関数で、G2について減少関数(資本が地域2の方に移動しちゃうから)。
そして生産関数が同一なので、企業2の資本需要関数は、
企業1の資本需要関数の、G1とG2を入れ替えただけの式となる。
注意なのが、地方政府は住民である労働者の所得を最大化するのが目的となるが、
資本税は課されない一方、労働者には一括税が課され、移転所得も無いので、Ti=Giより、
∂F(Ki,1,Gi)
Ii=F(Ki,1,Gi)-────────・Ki-Gi i=1、2
∂Ki
資本需要関数(G1とG2のみの関数)を代入してKiを消し、操作変数はGiなので、∂Ii/∂Gi=0と置く。
例えばI1をG1で偏微分するときは、G2はいったん所与(定数)とする。
Iiも消せて、G1とG2の方程式(最適反応関数)となる(所与とした方は変数に戻る)。
地域1と2の最適反応関数も、G1とG2を入れ替えただけの式となる。
後は最適反応関数同士を連立させて、ナッシュ均衡(交点)を求めると、
G1=G2=G#
求まったナッシュ均衡であるG#を用いて、資本需要関数からK1とK2を求め、
最終的に求まったI1とI2の合計を、
I1+I2=I#
とする。ナッシュ均衡がパレート効率的かどうかを調べるために、
2つの地域が競争せずに協力して、住民(労働者)の所得の合計を最大化してみよう。目的関数は、
I1+I2=I*
I*をG1で微分して0と置いたものと、I*をG2で微分して0と置いたものは、まったく同じになるので、
最適反応関数が1本になる。無限の組み合わせの中から、仮にG1=G2=G*を選ぶと、
G*<G#
I*>I#
となることが示される(具体的な数値例とグラフは教科書を参照)。
企業を誘致するための補助金競争も過大均衡となる。一方、住民(労働者)も移動可能として、
住民向けの公共支出(教育や医療・福祉など)は、正反対の結果となる。
公共支出を賄うための租税負担が高くなってしまう高所得者(優秀な労働者や企業)が移動してしまうので、
福祉支出の切り下げ競争になるとのこと(もちろんこれまでと同様にパレート非効率的な過少均衡となる)。
結局、生産要素(労働や資本)の移動性を考慮すると、上記のように外部性(市場の失敗)が必ず発生する。
外部性と来れば内部化で、合併して共同で課税や公共支出を行うことだが、
そうなると究極的には中央政府による集権制になってしまう。地方分権性もメリットがあるので難しい問題となる。
EUでは租税協調という一種のカルテルを形成しようとしているが、なかなか難しいらしい。
理由は、各国家間の規模の違いで、規模の大きなドイツやフランスは便益を享受、
規模の小さい新加盟国などは損失を被るとのこと。
・ 10章の最後、P250~P251、水平的外部性を内部化するための定率補助金政策。
すべてを中央集権制にしてしまうのも無理があるので、地方分権性を維持しつつ、
財政的外部性を内部化する方法として、中央政府からの定率補助金政策を、
10章3節の水平的財政外部性のモデルで分析してみよう。
中央政府は、地方政府の公共支出Giに対して、s×100%の補助金を出すとする。
地方政府の予算制約式:(1-s)Gi=tiKi
10章3節のモデルでは、Gi=移転所得なので、
∂F(Ki,1) ti
Ii=F(Ki,1)-───────・Ki+────Ki ・・・10.10
∂Ki 1-s
後は同じ手順。資本需要関数を代入してKiを消し、操作変数であるtiで偏微分して0と置くと、
最適反応関数が求まるので交点を求めると、
tC=tL=sの関数
地方政府同士が協力して一緒に税率を上げなくても、競争状態のナッシュ均衡の税率に定率補助金を出すことで、
税率を同時に上げてやる効果が生まれる。結果、住民の所得(厚生)も増加し、パレート改善できることが示される。
○ 11章、ネットワーク外部性
FAXの例が有名で、利用者数が増えれば増えるほど、便益が高まる財。需要側の規模の経済とも言える。
個人の効用が、同じ財を消費する他人の人数に影響を受けるという意味で、外部性がある。
他の例として、同じワープロソフトを使う人が増えると、文書ファイルの互換性の心配が無く、
入門書の発行が多くなったり、困ったときに周りで助けてくれる人が増えたり。
本書ではスマホを例に採り、アイフォンとアンドロイドの話で説明している。
・潜在消費者=1000人
・留保効用(留保価格=限界支払意思額)Vは、見事なまでに全員異なり、100円刻みで、
10万円>9万9千900円>9万9千800円>・・・>千円となっているとする。
縦軸にV、横軸に人数、左から留保効用の高い順に並べると、
i番目の人の留保効用Vi=10万-100(i-1)=100100-100i ・・・11.1
価格をPとすると、Vi≧Pの人達は購入する(等しい場合は購入する・しないは無差別だが、購入すると仮定)。
i番目の人まで購入するということは、i=701ならば、需要量もそのまま701となる。
Vi=P → 10万100-100i=P → i=1001-(P/100) ・・・11.A
価格を3万円とすると、i=701となる。すなわち、11.A式はそのまま需要関数となる。
ただし、上記の話ではまだネットワーク外部性を考慮していない。
N=すでにアイフォンを購入している人の数
ネットワーク外部性とは、消費者数が増えれば増えるほど、その財を消費している人の効用が高まる。
逆に消費者数が少ない内は、ネットワーク外部性が無い財と比べて、かえって効用は低くなる。
その境界を100人とし、ネットワーク外部性による効用の増加を単純にN倍とすると、
ネットワーク外部性を考慮した限界便益=(N/100)Vi
Vi≧Pという基準は次のように変わる。
(N/100)Vi≧P ・・・11.B
新基準11.B式の下では、購入者数が100人未満のときには、他社の携帯電話との接続が多くなり、
通話料金の割引を受けられなかったり、アプリが少なくて、Viより小さくなる。
逆に100人以上に購入者が増えれば、元のViより大きくなる。
元々、留保効用は11.1式なので、ネットワーク外部性を考慮した上で、
改めて(逆)需要関数を導出するには、(N/100)Vi=Pとして、11.1式を代入すると、
(N/100)(10万100-100i)=P → N(1001-i)=P
ここで変数iは、購入者数Nと書き換えることができるので、(逆)需要関数は結局、
P=(1001-N)N ・・・11.2
興味深いことに、11.2式は「2次関数」となり、一般的に複数均衡となる(A点とB点)。

もし市場価格P=3万円だったときの需要量は、
3万=(1001-N)N → N^2-1001N+3万=0
という2次方程式を解いて、Na=30.925、Nb=970.07という2つの解が得られる。
複数均衡と来れば、均衡の安定性の問題である。
まず低位均衡のA点について。30人未満の場合、例えば1番目の人は、留保効用10万円なのだが、
ネットワーク外部性を考慮した効用は、次のように千円となり、市場価格3万円より低いので購入しない。
(N/100)Vi → (1/100)10万円=千円
ところが、もし30人がすでに購入していると、31人目の効用は、市場価格3万円より高いので購入する。
(31/100)×9万7千円=3万70円
32番目以降の人も、次々と同様の理由で購入していく。
このような現象を、皆が持っているので自分も買うという行動=バンドワゴン効果と呼ぶ。
ただし、潜在消費者1000人の全員が買うわけではないことに注意。
購入者が増えるほど、ネットワーク外部性は確かに大きくなるが、
一方で消費者の留保効用Viは、100円ずつ小さくなっていくので、
ネットワーク外部性を考慮した限界便益は、次第に頭打ちとなる。
さて、問題の均衡の安定性についてだが、何かの拍子にA点よりほんの少しでも左側が実現してしまうと、
購入者数はどんどん減り続けて、最終的にゼロとなる。
一方、A点以上になると、今度はどんどん購入者が増え続ける。
どちらも、どんどん離れて行くので、均衡点Aは不安定である。
この均衡点Aは、クリティカル・マスと呼ばれる(つまり臨界点)。
いったんクリティカル・マスを越えれば、雪だるま式に購入者が増えるので、独占市場になりやすい。
一方、高位均衡のB点の安定性はどうだろうか?
B点より左側のときには、人数がどんどん増えるのでB点に近づいていく。
しかしB点を越えると、ネットワーク外部性を考慮しても、市場価格>限界便益となって購入しない。
そのため、B点より右側では、人数がどんどん減るので、やっぱりB点に近づいて行く。
すなわち、均衡点Bは安定である。
何かの拍子にB点より左側や右側にちょっと動いてしまったとしても、また元のB点に戻る力が働くからだ。
・ まずはマーケットシェアの確保
市場価格P=1万円にすると、クリティカル・マス=10.092となるので、クリティカル・マスを越えやすくなる。
そこで各企業は、ネットワーク外部性のある財を売り出すときに、
その市場における自社製品の顧客数を確保するために、しばしば無料(や低価格)キャンペーンを行う。
市場の立ち上がり段階や、新規参入企業は、最初に売り出した時点でどれだけ顧客を確保できるかによって、
独占企業となれるか退出せざるを得ないかが決まってくる。
・ ネットワーク外部性と来れば、「標準化」
規格が統一(標準化)されていると、ハードウェア(機器)にしろ、ソフトウェアにしろ、
繋げやすかったり、互換性(置き換えやすい)があったりして便利ではある。
ソフトの互換性で思い付くのがPDF形式の文書ファイル。
しかし、一方で独占の弊害も発生し、特に過剰慣性(ロックイン効果)が、独占状態を存続させやすくする。
過剰慣性(ロックイン効果)とは、消費者が1つの規格やネットワーク・サービスに慣れ親しんでしまうと、
他の規格に切り替えにくくなるというもの。
切り替えるのに大変な心理的負担や、時間・労力が必要となるし、
例えばOSを変えるとなると、互換性のあるアプリケーションソフトまで換えなければならなくなり、
それまで持っていたソフト資産がすべて無駄となる。
このような費用を、スイッチング費用(転換費用)と呼ぶ。
スイッチング費用の存在が、過剰慣性(ロックイン効果)を生み、
その結果、より高い社会厚生を実現するような新技術や、品質の高いネットワーク財を供給しようとする企業の、
新規参入が困難となる。
かといって、政府の所轄官庁などの規制当局が、強制的に新規格を基準化するのも、なかなか難しいだろう。
・ 補完財(ヴァリアンの入ミク(9版)の36章「情報技術」より)
ネットワーク外部性とは定義的に異なるが、似たような問題を持つのが補完財。
靴は左足と右足の両方があって初めて役に立つ。
DVDソフトとDVDプレーヤー、CPUとOS、OSとアプリケーションソフトなど。
補完関係にある相手の財の価格が低下すれば、自分の収入(利潤)が増える。
ゲーム理論的状況(戦略的相互依存関係)になっていることが、この時点でわかる。
家電メーカーは、利用可能なコンテンツが十分に生産されると保証するまで、DVDプレーヤーを作りたがらないし、
逆にソフト会社は、DVDプレーヤーが十分に普及されるまで、コンテンツを作りたがらない。
合併するかどうかはともかく、結合利潤を最大化するように行動できれば、クリティカルマスを超えやすい。
また、規格を統一(標準化)することは、競争を激しくすることで、補完財の価格を下げる効果もある。
OSの会社から見れば、ハードウェアの規格が統一されれば、OSの生産が容易になるだけではなく、
ハードウェア産業に競争圧力を生む。
● コースの定理
http://jairo.nii.ac.jp/0047/00000352
コースの定理は本当に成立するのか (1)
http://jairo.nii.ac.jp/0047/00000319
コースの定理は本当に成立するのか (2)
同内容が次の教科書に載っていて、さらに上記ファイルには無い説明もある。
「中村竜哉 法と経済学 企業組織論に係る分析手法の研究 白桃書房 2010/12」
コースの定理というのはスティグラーが名付けたもので、コース自身ではない。一般的にコースの定理は、
1:権利の配分と、パレート効率的な資源配分(生産パターン)は無関係である。
ただし、所得分配には影響を与える。
ことを述べるものであるが、コース自身はそのような世界が現実に成り立つことを主張することが
目的だったわけではない。
2:現実には取引費用の存在から法制度が資源配分に影響を与える。
3:取引費用が大きすぎて市場取引が不可能な場合、外部性の問題は企業内取引(組織内)で解決される。
2と3の重要性を主張するのがコース自身の目的で、
経済学の分野では後々、2は法と経済学、3は組織の経済学へと発展する。
○ スティグラーの解釈(ファイル1の2.1、教科書の4章8節)
まずコースの定理を説明する時によく出てくる例として、工場とクリーニング店の例と、農場と牧場の例が有名。
前者は、工場の出す煙がクリーニング店の洗濯物を汚すという外部不経済の例。
後者は、先にある土地で農場を営んでいた隣に、牧場が出来た結果、
牛が隣の農作物を食い荒らしたという外部不経済の例。
どちらのケースも理不尽に思えるかもしれないが、権利配分を考えるということは、
逆に(先着順含めて)どちらも権利なしの状態から考察を始める。
例えば農場と牧場のケースでは、牧場の方が加害者と思ってしまうが、
どちらにも権利なしの世界では、牧場主の立場から見れば、勝手に牧草地を農場に変えられたとも言える。
次の表(ファイル1の表1、教科書の表4(p95)および表12(p142))の数値例を用いると、
「牛を1頭増やすごとの限界収入>農場の限界損害」である限り、牛は増やした方が社会的に効率的である。
牛の数 | 牧場主の収入の総額 | 農場主の損害の総額
──────────────────────────
9頭 | 94ドル | 0ドル
──────────────────────────
10 | 100 | 2
──────────────────────────
11 | 105 | 3
──────────────────────────
12 | 109 | 6
──────────────────────────
13 | 111 | 10
──────────────────────────
14 | 112 | 15
──────────────────────────
15 | 111 | 21
──────────────────────────
12頭→13頭にしたときの、
牧場の限界収入=111-109=3
農場の限界損害=10-6=4
となって、そこで初めて、牧場の限界収入<農場の限界損害となる。
社会的に見れば牧場の最適生産量は牛12頭である。
取引費用が0で、交渉が可能である限り、この最適生産量は変化しない。
牧場主が自分のことだけを考えれば、14頭までは限界収入が正なので、
14頭まで生産量を増やすことが最適なのではと思うかもしれないが、コースの定理ではそうならない。
交渉によって取引が行われるからだ。
権利の配分は、生産活動が終わった後の所得分配については影響を与えるが、
生産に関する条件である限界収入や限界損害には影響を与えない(需要の所得効果が0ならば)。
すなわち上記の表1そのものは、権利の配分によっては変化しない。
もし放牧の自由の権利を認めた場合は、農場に権利があるときと比べて確かに農場主の所得は減る。
しかし交渉による取引を考慮すると、権利は牧場側にあるので、農場の方が牧場に対して
生産量を減らしてくれと頼む形で交渉が行われる。
農場が牧場に14頭から13頭に減らしてくれと頼むと、牧場側で減る収入は112-111=1ドルなので、
1ドルを補償費用として支払えばいい。
その結果、農場側では損害額が15-10=5ドルも減る。差し引きで4ドルも損害額を減らせる。
一方、社会全体で効率的な水準である12頭の状態で、農場側はまだ6ドルの損害が出てるので、
さらに11頭に減らしてくれと牧場に頼んだ場合、それで減らせる農場側の損害額は
6-3=3ドルにしかならないが、牧場に支払う補償費用は109-105=4ドルになる。
逆に農場側に権利がある場合、今度は牧場側が農場に対して生産量を増やさせてくれと頼む形で交渉が行われる。
同じような類推(アナロジー)によって、最適生産量は結局12頭となる。
お互いの限界収入と限界損害を比較考量して、初めて社会全体の効率的な水準を導出できるのだ。
コースの定理は一見冷たいように思えるかもしれない。
しかし、もし農場主と牧場主が結婚したらと考えれば何も心理的抵抗はない。
そこで結合利潤を考えることが、効率的水準を明らかにすることを、下記の生産の外部性で説明する。
○ まずは消費の外部性とコースの定理を、林公共の説明で紹介
https://sites.google.com/site/publicfinanceuoftokyo/toppage/public-finance-law
で、公開されている林先生のノートの、ファイル07の図4-1。教科書では4章。

喫煙家Aと嫌煙家Bの例で、AがBに外部不経済を与えている。タバコの消費量=Z、タバコの価格=p。
Aの限界便益=限界便益MB(Z)
Bの限界損害(限界外部費用)=MD(Z)
Aの(純)限界便益:限界便益MB(Z)-p
Aにとっての私的限界費用=p
社会的限界費用=p+MD(Z)
パレート効率的なのは、pを原点と考えて、MB(Z)とp+MD(Z)の交点Cで、最適消費量=Z*。
そのとき、Aの純便益CD=Bの限界損害FZ*、になる。
ケース1:Aに喫煙権がある場合、MB(Z)=pとなる消費量Zバー(Z*以上の過剰消費量)となる。
ケース2:Bにきれいな空気を吸う権利がある場合は、Z=0となる。
消費量は権利の配分で変化しているように見える。
ところが、ケース1ではBがAに補償してZを減らしてもらえば、
Z*より右側ではCD<FZ*なので、補償費用CD以上に限界損害が減るのでBにとって得となる。
ケース2では、AがBに吸わせて欲しいと補償すれば、
Z*より左側ではCD>FZ*なので、補償費用FZ*以上に限界便益が増えるのでAにとって得となる。
純粋交換経済のエッジワースボックスを思い出そう。外部性がなければ市場価格だけを見て、
分権的に意思決定するだけで、後は取引(交渉)を通じて勝手にパレート効率的になる。
逆に、消費の外部性(市場取引を通じずに効果が市場の外に及ぶ)があると、パレート効率的にならない。
外部性があるというのはその外部効果を取引する市場がないということであり、
それは所有権が設定されていないことを意味する。喫煙の例で言えば、空気の所有権を設定するのは不可能に近い。
所有権が無ければ、取引だって発生しないのは自明である。
みんなが他人の持ってる物も俺の物だと思ってるジャイアンになる。
しかし、所有権さえ確定されれば、たとえ外部性があっても、後は取引(交渉)を通じて内部化される。
それこそがコースの定理の本質なのである。そしてその権利をどちらに配分しようと結果は同じになる。
パレート効率的水準(資源配分)は不変となる。
ただし、資源配分には影響を与えなくても、所得分配の結果には影響を与える。
例えばケース1の方が、Aにとって所得分配の結果は有利であるから、喫煙権を主張するだろう。
図4-1はコースの定理を説明するときによく用いられる図だが、成立するためには条件が必要で、
条件1:取引費用が小さくて交渉可能
条件2:需要の所得効果がゼロ(すなわち準線形効用関数を仮定)
準線形効用関数(準線形選好)については、 ミクロ経済学ノートを参照。
所得効果が存在すると、補償を支払った時点で、MB(Z)やMD(Z)そのものがシフトしてしまう。
そのため、パレート効率的水準(Z*)そのものが定まらない。
さらに林公共や柴田公共では、コースの定理も柴田のダイアグラムを使って説明している。
林公共の図4-10(本ノートの林公共の章を参照)では、2つのレンズが描かれている。
AとBのどちらに権利を配分するかによって、レンズ内で成立するパレート効率的水準は
Z1~Z2の範囲か、Z3~Z4の範囲に別れる。
AとBの無差別曲線同士が接する契約曲線KK’は斜めになっているが、
もし需要の所得効果が無ければ、契約曲線KK’は垂直となり、最適消費量Z*は1つに決まる。
○ ヴァリアンの入ミク(9版)の35章「外部性」から、生産の外部性
川上の工場Sが、川に汚染水xを流すことで、川下の漁場Fに外部被害(外部不経済)を与えているとしよう。
工場の生産量をs、漁師の生産量をf、
工場Sの費用関数をCs(s,x)、漁師の費用関数をCf(f,x)、
∂Cs/∂x<0、∂Cf/∂x>0とする。
工場Sから見て、汚染水xを川に流した方が費用を節約でき、逆に汚染水を川に流さないようにするには、
余計な費用が掛かることを意味する。
・ 権利が確定しておらず、工場Sが汚染水を勝手に川に流すケース1
工場Sの利潤関数:Ps・s-Cs(s,x)
漁師Fの利潤関数:Pf・f-Cf(f,x)
汚染水xは工場がコントロールするので、それぞれの利潤最大化条件は、
工場Sの利潤最大化条件:Ps=∂Cs/∂s と 0=∂Cs/∂x
漁師Fの利潤最大化条件:Pf=∂Cf/∂f
工場Sは汚染水の限界費用が0になるまで川に垂れ流し、漁師Fはそれを見ていることしかできない。
∂Cf/∂x>0なのだが、工場Sは無視している。社会的限界費用が考慮されておらず過剰生産。
・ 合併して結合利潤を考えるケース2
結合利潤:Ps・s+Pf・f-Cs(s,x)-Cf(f,x)
利潤最大化条件は、操作変数がs、f、xの3種類なので、
Ps=∂Cs/∂s
Pf=∂Cf/∂f
∂Cs/∂x+∂Cf/∂x=0 → -∂Cs/∂x=∂Cf/∂x
3本目の式が重要で、ちゃんと漁師への限界被害∂Cf/∂xを考慮に入れている。
両者に発生する限界費用の和=社会的限界費用が考慮されており、パレート効率的である。
・ 権利が確定しており、漁師Fが川を汚染されない権利を持つ。xを1単位、qの価格で取引できるケース3
工場Sの利潤関数:Ps・s-qx-Cs(s,x)
漁師Fの利潤関数:Pf・f+qx-Cf(f,x)
漁師の方もxの権利を何単位売るかコントロールできるので、利潤最大化条件は、
工場Sの利潤最大化条件:Ps=∂Cs/∂s と q=-∂Cs/∂x
漁師Fの利潤最大化条件:Pf=∂Cf/∂f と q=∂Cf/∂x
ケース2と同じ結果となる。
・ 権利が確定しており、工場Sがx#だけ放流できる権利を持つ。xを1単位、qの価格で取引できるケース4
ちょっと複雑になる。
工場Sの利潤関数:Ps・s+q(x#-x)-Cs(s,x)
漁師Fの利潤関数:Pf・f-q(x#-x)-Cf(f,x)
工場Sにとって放流できるのはx#までなので、それを超えるxは漁師Fに補償することになる。利潤最大化条件は、
工場Sの利潤最大化条件:Ps=∂Cs/∂s と q=-∂Cs/∂x
漁師Fの利潤最大化条件:Pf=∂Cf/∂f と q=∂Cf/∂x
ケース2およびケース3と同じ結果になる。すなわち授権方法と最適生産量は無関係で、
パレート効率的な資源配分の水準は不変というコースの定理。
・ 35章5節「市場シグナル」
合併すれば結合利潤は最大化される。ということは、もし合併していなければ、利潤の合計は結合利潤より低くなり、
必ず買収圧力が働く。買収しようとするのが誰であれ、買収すれば必ず儲かるからだ。
従って利潤最大化というインセンティブによって、ほっとけば勝手に外部性は内部化される。
○ レントと準レント
ミクロ経済学ノートを参照。
○ ファイル1の3.1節、教科書の5章4節
小麦の生産量=w
牛肉の生産量=m
小麦の価格=5
牛肉の価格=10
小麦の費用関数:Cw=0.5w(1+w)
牛肉の費用関数:Cm=0.5m(11+m)
小麦への損害「量」(額ではないことに注意)をdとすると、
d=0.1mw
牛の量が一定でも、小麦が増えれば小麦への損害量自体は増えるという関係を意味する。
では、共同経営による結合利潤を考えよう。損害「額」=5×d=0.5mwであることに注意すると、
結合利潤π=πw+πm-5d ・・・1
=5w-Cw + 10m-Cm - 0.5mw
結合利潤を最大化する小麦と牛肉の最適生産量は、
∂π/∂w=5-0.5-w-0.5m=0 ・・・2A
∂π/∂m=10-5.5-m-0.5w=0 ・・・2B
内生変数2個で、方程式が2本なので解が求まる。結果、w=3と、m=3になる。
結合利潤=総収入-総費用-小麦の損害額
総収入=3×5ドル+3×10ドル=45ドル
総費用=(0.5×3×4)+(0.5×3×14)=6+21=27ドル
小麦の損害額=5ドル×0.1×3×3=4.5ドル
共同経営で発生する結合利潤は、13.5ドルである。
最適生産量のw=3と、m=3から、wやmをどう変化させても結合利潤は減ってしまうことを確認してみよう。
そこでもし小麦と牛肉が異なる経営者によって個別に経営された場合、
農場に権利を付与すると、最適生産量が変わるかどうかを調べてみよう。
例えば農場が損害額について、どうせ賠償してもらえると思って気にせず利潤最大化を行うと、
∂πw/∂w=5-0.5-w=0 → w=4.5
農場の利潤=5ドル×4.5-0.5×4.5×5.5=22.5-12.375=10.125 ・・・3
これだけを見ると、権利が農場に付与されれば、農場は生産量を増やしそうに見える。
ところが、損害賠償責任を考慮に入れた牧場が利潤最大化を行うと、
πm♯=πm+5d
∂πm♯/∂m=10-5.5-m-0.5w=0 ・・・4
w=4.5を所与とせざるを得ないので、4式に代入すると、
m=2.25
牧場の利潤=10ドル×2.25-0.5×2.25×13.25-5×0.1×4.5×2.25
=22.5-14.90625-5.0625=2.53125 ・・・5
農場の利潤と合計しても、13.5ドル未満となってしまう。
こうなると、どういう交渉が起きるだろうか?
小麦の生産量を4.5から3へ減らしてくれと牧場主が頼むと、
農場の利潤は9ドルとなって1.125ドル減る。
しかし牧場はその分、4式においてm=3にできて、利潤は30-21-4.5=4.5ドルになる。
すなわち牧場の利潤は1.96875ドル増える。
そうすると、農場の減った利潤1.125ドルを補償して、
まだ牧場主には0.84375ドルの利潤の増加が見込める。
結合利潤がw=3と、m=3のとき最大であるということは、
それ以外の生産量を選んでる状態から、最適生産量にすることで必ず補償ができるのだ。
結局、農場に権利を付与した場合、結合利潤の最大化において、wで偏微分した時だけ、
損害額(5d)を認識しないことを意味するので、
∂π/∂w=5-0.5-w=0 ・・・2A’
∂π/∂m=10-5.5-m-0.5w=0 ・・・2B
となることを意味する。しかしこれは結合利潤を最大化する条件とは異なる。
共同経営で発生する結合利潤は、13.5ドルが最大なのだから、
2B式はともかく2A’式のような最適化では必ずそれ以下になる。
だったら、交渉によって最適生産量より低い方が、最適生産量より多い方に減らすように頼めば、
多い方で減った利潤を、低い方で増えた利潤で必ず補償できる。
結合利潤=総収入-総費用-小麦の損害額
という式自体は、権利の付与の仕方に関わらず不変なので、
共同経営じゃなくても取引費用がゼロで交渉が可能であれば、これを最大化する最適生産量が必ず実現できる。
これまでの結果を、今度は牧場に権利を付与した場合について考察してみよう。
今度は牧場主が損害額(5d)を認識しないので、結局、
∂π/∂w=5-0.5-w-0.5m=0 ・・・2A
∂π/∂m=10-5.5-m=0 ・・・2B’
2B’式から、m=4.5となる。
牧場の利潤=10ドル×4.5-0.5×4.5×15.5=45-34.875=10.125
農家はm=4.5を所与とせざるを得ないので、2A式より、w=2.25
農場の利潤=5ドル×2.25-0.5×2.25×3.25-0.5×2.25×4.5
=11.25-3.65625-5.0625=2.53125
農場に権利があったケースに対して、見事に数値が対称となっている。
農家が牧場主に対して牛肉の生産量を4.5から3に減らしてくれと頼めば、
牧場主の利潤はやはり同じ9ドルとなり、1.125ドル減る。
一方、農家が小麦の生産量を3に増やせば、こちらも見事に利潤は4.5ドルになり、
利潤は1.96875ドル増えるので、補償できる。
○ コースの定理が成り立つ条件、成り立たない条件。
さて、取引費用がゼロで交渉が可能であれば、権利の付与に関係なく「必ず」最適生産量になると言ったが、
実はかなり特殊な数値例の下でのみ成立する。
もし違う数値例であれば、成立しないのである(D.L.Shapiro [1974])。
それぞれの総費用関数を次のような数値例に変えてみる(7という固定費用を追加)。
小麦の費用関数:Cw=7+0.5w(1+w)
牛肉の費用関数:Cm=7+0.5m(11+m)
後は結合利潤の式を作って、mとwで偏微分してそれぞれの最適生産量を求めてみると、
追加された「+7」の部分は偏微分の過程で消えるので、最適生産量は相変わらず、w=3と、m=3である。
総収入は相変わらず45ドルであり、小麦の損害額も4.5ドルのままであるが、
総費用が27ドルから41ドルに増える(その差は14)。
結果、結合利潤は最適生産量であっても-0.5ドルとなる。
最大でマイナスなのだから、最適じゃない生産量から最適な生産量に変化させることで
増える利潤で補償費用を賄うなんてどちらにしろ不可能である。
つまり、コースの定理はもはや成り立たない。結局、外部不経済(ここでは小麦の損害額の5d)を
カバーする(内部化する)利潤や所得を生み出している条件の下でのみ、コースの定理は成立するのである。
補償するということは、相手の持っている権利を購入していることに他ならないわけで、
権利という財を買うときには、予算制約に縛られる。
資源配分が不変どころか、そもそもパレート効率的水準すら達成できない。

林公共の図4-10で言えば、Aにタバコを吸う権利があるF点から出発して、
タバコの煙に対する需要の所得効果が0で、例えば契約曲線KK’がZ3の水準で垂直だったとしよう。
_ _
Aの無差別曲線VAに沿って、Zから出発して左のZ3までAに移動してもらうには、
Aの予算制約線であるHJ線からκ点までの垂直距離の分だけ、Bが補償しなければならない。
ところが、Bの所得(線分OBH)がその垂直距離より短いと、所得を全額使って補償しても、Z3まで移動できない。
それでも、パレート改善できるレンズ内の色が付いた部分が、まだあるかもしれない。
Z3までは行けなくても、少なくともZバーよりは左に行けるかもしれない。
しかし、それは契約曲線上ではないので、パレート効率的とは言えない。
柴田公共の所でも話したが、忘れがちだけど重要な問題なのが、端点解のケースである。
また、Regan(1972)が指摘するように、長期的には準レントは0となり、生産要素に対する機会費用を
稼ぎ出すだけとなる(長期的に経済学的な利潤は0となるので、補償する余裕などない)。
○ ファイル1の3.1節に無い説明を、教科書から紹介(p135~p138と表10)
Coase(1988)は次のようなケース(表10)を用いて、コースの定理が成り立つと反論している。
まず準レント(財市場の生産者余剰)ではなく、農家と牧場主のレント(生産要素市場の生産者余剰)を用いる。
農家のレント:a
牧場主のレント:b
被害額:c
ケース1:農家の稼ぎ出すレントを100ドル、牧場主のレントも100ドル、被害額を50ドルとしよう。
牧場主に損害賠償責任がある場合、レントから50ドルを支払って、まだ操業を続けるだろう。合計は150ドル。
責任が無い場合、農家のレントが50ドルとなって、まだ操業を続けるので、資源配分は不変。合計は150ドル。
ちょっと飛んでケース4:農家のレントは30ドル、牧場主のレントは40ドル、被害額は50ドルのまま。
牧場主に損害賠償責任がある場合、賠償をするより農家に30ドル払って操業を辞めてもらった方が安くつく。
牧場のみが操業し続けて、農家は働かずに30ドルを得て、牧場は10ドルとなり、合計40ドル。
責任が無い場合、農家は被害額がレントを上回るので操業停止し、牧場のみが操業。資源配分は同じ。合計40ドル。
ケース5:農家のレントは40ドル、牧場主のレントは30ドル、被害額を50ドル。
農家と牧場主の立場がケース4と逆になる。資源配分は同じで、合計40ドル。
特に(5,なし)のケースでは、今度は農家の方が牧場を買収する。
表10 ─────────────────────────
│ 牧場主に責任あり │ 牧場主に責任なし │
────────────────────────────────
│a=100│ 双方が操業を続ける │ 双方が操業を続ける │
1│b=100│農家100、牧場主50│農家50、牧場主100│
│c=50 │ 合計150 │ 合計150 │
────────────────────────────────
│a=25 │牧場のみが操業を続ける│牧場のみが操業を続ける│
2│b=100│ 農家25、牧場主75│ 農家0、牧場主100│
│c=50 │ 合計100 │ 合計100 │
────────────────────────────────
│a=100│農家のみが操業を続ける│農家のみが操業を続ける│
3│b=25 │ 農家100、牧場主0│ 農家75、牧場主25│
│c=50 │ 合計100 │ 合計100 │
────────────────────────────────
│a=30 │牧場のみが操業を続ける│牧場のみが操業を続ける│
4│b=40 │ 農家30、牧場主10│ 農家0、牧場主40 │
│c=50 │ 合計40 │ 合計40 │
────────────────────────────────
│a=40 │農家のみが操業を続ける│農家のみが操業を続ける│
5│b=30 │ 農家40、牧場主0 │ 農家10、牧場主30│
│c=50 │ 合計40 │ 合計40 │
────────────────────────────────
(3,なし)のケースでは、農家が牧場主に25ドル渡して操業を停止してもらう。これは理解できるが、
(2,あり)のケースでは、牧場主の損害賠償額は25ドルで、農家は操業停止と説明している。
たぶん、牛の潜在能力はMAXで50ドル分の農作物を食い荒らせるが、そもそも25ドル分の農作物しかないので、
損害賠償は25ドルでいいということか。
さて、ケース4と5は、損害賠償に関してはレントが足りないので不可能だが、相変わらず相手を買収できている。
予算制約に縛られて(予算制約がバインドして)いないケースを持ち出しており、反論になってないと思う。
例えば表10の(4,あり)のケース。他の仕事(漁業)のレントが30だったとしよう。
農家を買収しつつ牧場で働けばレントは10ドルだが、牧場主はそれでも農家を買収するのだろうか?
あるいは、お互いのレントが30だったらどうするのだろうか?
牧場主に責任ありの場合、牧場主は働いて稼いだ30ドルで農家を買収し、最終的にレントは0ドル。
農家は働かずに30ドル・・・。しかも牧場主は毎月・毎年農家にレントを払わなければならない。
面白いのが、表を縦に見ること。一見この表では、権利配分によって資源配分は変化していない。
ケース4で横に見れば、牧場主の責任の有無によって、どちらも牧場のみが操業しているし、
ケース5で横に見れば、権利配分によらず、農家のみが操業している。
ところが、(4,あり)のケースと、(5,あり)のケースを比べてみよう。
権利配分は同じだが、農家と牧場主のレントが違う。すなわち、所得分配が変化すると資源配分も変化する。
牧場のみ操業→農家のみ操業となっている。そこで需要の所得効果0の話に移ろう。
○ 所得効果(富効果)。ファイル1の3.2、教科書の5章5節。
これに関しては、林公共の所で散々説明しているので、コースによる反論をいきなり紹介しよう。
Coase(1988)による反論は、ファイルの方には無く、教科書の方にしかない。
さまよえる牛のケースを用いよう。Demsetz(1972)によると、例えば農家は小麦で作られたパンの方が好きで、
牧場主は牛肉の方が好きだとしよう。
そこで権利配分が農家に有利となれば、農家の所得が増えて牧場主の所得が減る。
小麦の需要は増えて価格は上昇し、牛肉の需要は減って価格は下落するだろう。
すなわち、権利配分によって所得分配が変化したとき、牛肉や小麦に対する需要と価格が変化する可能性があり、
さまよえる牛のケースの表(限界収入および限界損害)そのものが変化してしまうのだ。
コースによる反論は、農家と牧場主の両者とも、土地は自己所有ではなく、借地とする。
そして両方の土地は、1人の地主によって所有されているとしよう。
この場合、牛肉と小麦に対する需要および価格の変化は、そのまま土地の均衡賃貸料に反映され、
農家の賃貸料は上昇し、牧場主の賃貸料は下落するので、両者の所得分配は変化せず、地主の所得も変化しない。
地主が1人なおかげで、農場と牧場は間接的に共同所有しているような形になっているので、
両者の間で発生した所得分配の変化は、相殺されることになる。
しかしこのコースの反論の仕方も、前節と同様に反論になってないと思う。
需要の所得効果が0じゃない状態で、所得分配が変化したらどうなるか?と聞いているのに、
そもそも最初から所得分配が変化しないケースを持ち出すのは、本末転倒である。
コースに対する再反論は、地主が別々だったら?で終わりな気がする。
牧場の地主は牛肉が好きで、農場の地主はパンが好きで・・・。
あるいは賃貸料の下がった牧場には貸さず、マンションを建てるかもしれない。
そもそもコース自身、前節の表10で、所得分配の違いで資源配分が違うことを説明している。
○ ファイル1の3.3、教科書の5章7節、「参入・退出の自由」
最初はAに責任が割り当てられている状態から、ルール変更によってBに責任が割り当てられたとしよう。
BがAに生産量を減らしてくれと頼む形で交渉が行われ、変更後にAの利潤は増えて、Bの利潤は減る。
法と経済学ノートに頻繁に出てくる、 Carabresi(1965)よると、(上記の漁業の例のように)機会費用を考えた場合、
他の産業における生産要素の収益率は均等化するので、
(生産のパレート効率性の話で、例えばX財産業とY財産業と労働市場の均衡を考えると、
Px・MPLx=W=Py・MPLyとなる)
長期的にAの産業には参入が、Bの産業では退出が起きて、資源配分は変化し、コースの定理は不成立。
Zerbe(1976)(1980)によると、そのような批判は間違っていて、
ルール変化前はAの支払う損害賠償金が限界費用に含まれており、変化後にはAが生産拡大を諦める代わりに、
受け取る損害賠償金が含まれるので、利潤が増減することは無いらしい。
ちょっと分からない。ファイル1の3.1節、教科書の5章4節の、小麦と牛肉の数値例によると、
どう考えても利潤は変化している。
○ ファイル2の3.6.2、教科書の5章10節2項、「財産権ルールとコスト関数」
これの1つ前の、ファイル2の3.6.1、教科書の5章10節1項の最後より、
取引費用と所得効果が無いケースを引き続き扱っている。
Aが被害企業、Bが加害企業とする。Frech(1979)によると、BがAに損害賠償責任があるルールと、
Aに外部性を発生させない所有権(財産権)があるルールとでは、結論が異なる。
法律上の責任ルールだと、短期においては(交渉によって)コースの定理は成立するが、
参入・退出がある長期においては、不成立となる。
ところが、所有権ルールならば、参入・退出がある長期においても、コースの定理は成立する。
ファイルの方も教科書の方も、説明が少なすぎて理解できなかった。
ファイルと教科書の双方とも式番号は同じで、5~8式の内、5式と6式は生産量のaとbでラグランジュ関数を
偏微分すれば導出できる。7式と8式は長期における参入と退出を考慮するので、企業数のnaとnbで
ラグランジュ関数を偏微分すれば導出できる。
それ以降がどういう設定なのか理解できない。特に財産権ルールの第4。
「参入企業にとって参入価格は均衡において限界費用に等しく、他に転嫁できないので限界費用は0となる。」
どういうことなのか分からないが、少し戻ってファイル1の3.3、教科書の5章7節の最後より、
結局は所有権ルールの下でも、所得効果がある場合、コースの定理は長期(参入・退出)においても不成立。
● 最後に回しておいた、林公共の10章と12章。
○ 10章、公的扶助と効率的な再分配。
個人的に林公共の中で一番好きな章で、給付の具体的な方法を詳しく検討している。
これまで、他の教科書を読んでいるときには、負の所得税はかなり性質が良くて、
なんで現実の世界でどこの国もやらないのだろうとずっと疑問を持っていたが、
本書で強調されている説明でやっと理由が分かった。
負の所得税は課税最低限以下の所得の人達に対して給付を行う(ベーシックインカムだと国民全員になる)。
これはちょっと考えただけでも、ものすごい給付総額になる。
財源をいったん確保する過程で、徴税コストや税率が影響を与える資源配分の歪みなどが、かなり大きくなる。
そこで次に考えられるのが、給付が本当に必要な低所得者層に限定する方法で、それなら財源確保も少なくて済む。
カテゴリーに分類してターゲットだけに給付を行うことをタギング(札貼り)という。
ところが今度はターゲット効率性という問題が生じる。
例えば低所得を基準にタギングを行うと、本当は働けるのにあえて働かず、給付を受けようとする者が現れる。
個人がそのように操作できるような基準でタギングを行うのは望ましくない。
本来、給付の対象となるべき層は、所得が低い人達ではなく、
障害者や母子家庭などの所得を獲得する能力が低い人達であろう。
所得だけを基準にしてしまうと、能力の高い人まで不正受給してしまう可能性がある。
獲得能力の高い人は、短い労働時間で高い所得を獲得でき、
低い能力の人が同じ所得を得るためには長時間労働が必要となる。
・ 10章4節、情報の非対称性。
タギングの効率性を高める上で問題となるのが、情報の非対称性である。
本来、基準とすべき所得獲得能力は、観察するにはかなり難しい。そこで所得を基準にせざるを得ない。
その前に、どういう記号を定義し、どういう図を描き、それをどう説明するかについて、
本書の10章はちょっと難しい。
よーく読んで記号や変数の意味を理解して、図とにらめっこしながら、慎重に何度も読まないと理解できない。
まず能力の高いAと低いBについて、効用関数には労働時間Hも負効用として入る。消費量をCとする。
効用関数はU=U(C,H)。
賃金率をWとすると、Y=WHとなるので、H=Y/Wとできる。
賃金率Wは個人にとって選択できず所与だが、能力の違いによりWa>Wb。
所得の高いAに税金T、それをBに所得移転。
可処分所得で消費するので、最終的に効用関数は変数Yだけで表現でき、
Ua=U(Ya-T,Ya/Wa) Ub=U(Yb+T,Yb/Wb)
タギングの方法1:所得制限
仮定1:同一の効用関数
仮定2:情報の非対称性から確認できるのは所得だけ。
Bの効用を最大化する所得をYb*、 _
給付が受け取れるか受け取れないかの基準となる所得制限をY(以下、Yバー)とする。
情報の非対称性から、Aは自分の所得をYバーに偽る。 Λ
そこで、Aの偽る前の効用関数をUa、偽ったときの効用関数をUa(以下、Uaハット)とする。

教科書のP307、講義ノートの方はファイル13、それぞれにある図10-7を見ると、
まずYバー=Yb*と設定してみて、横軸上のYバー=Yb*の水準で垂線を描くと、
まずUbの最高点にぶつかり(B点)、さらにその上の方でUaハットとぶつかる(A点)。
効用関数UaハットがUbの上方に位置する理由は、後で説明する。
Bにとって給付が受け取れて、なおかつBの効用水準が一番高いのはYb*なので、
政策当局はBのことだけを考えて、Yバー=Yb*とするのが望ましいように見えるかもしれない。
しかしB点でのBの効用関数は、効用最大化水準に位置するので、傾きはゼロ=平らである一方、
A点でのAの偽った効用関数は全然平らではなく、傾きはかなり急である。
そうすると、ほんの少し所得制限YバーをYb*より下げても、Bにとってはそんなに効用は減らないが、
偽っているAの効用は大きく下がる。
ここからがややこしいのだが、議論しやすいために、偽ってないときのAの効用最大化点をGとし、
たまたま、A=Gと同じ高さ(同じ効用水準)だったとしてみよう。
(同一の効用関数なのに、UbよりUaの方が右上に位置する理由も後で説明する。)
もしYバーをYb*より下げてみると、それに対応してA点からA’点に大きく下がり、Gの方が高くなるので、
Aは偽って働かないよりも、ちゃんと働くことを自ら選ぶ。
そこで出てくるのが自己選択制約式(グーグルで検索してみると、誘引両立制約と同じようだ)。
Λ _ _
Ua=U(Y+T,Y/Wa)≦U(Ya-T,Ya/Wa)=Ua ・・・1
1式の意味の前に、そもそもグラフ上で、偽ってる効用関数Uaハットが、
偽ってないUaよりも上方に位置している理由について。
偽っているUaハットは給付をもらっている一方で、偽ってないUaなんて、給付をもらえないどころか、
逆に税金を払っているので尚更だ。
もちろんUaハットはUbと比べても位置が高い。
Aが労働時間を減らして所得を偽っていても、賃金率がWa>Wbなので、
Bと同じ所得を得る上でBよりも少ない労働時間で済み、効用関数の中の労働の負効用がBよりも小さいため。
以上を踏まえれば、同質の効用関数でもUaがUbより右上に位置する理由もわかるだろう。
結局、図10-7は、横軸に所得Yを取って、効用関数を描いているので、
税金Tや、それぞれの賃金率WaとWbがパラメータとなる。
U字型になるのは、いずれ労働の不効用の方が上回るようになるから。
さて、1式が成り立つということは、どういう意味なのかを説明しよう。
働く時間を減らして偽ったときの効用(左辺)より、偽らずに長時間働いた方(右辺)が、
前者は給付がもらえて、後者は税金を払わなければならないとしても、それでも後者の方が効用が高いことを意味する。
もし1式が成り立てば、Aは自ら後者を選ぶということだ。
1式を外から制約条件として課しているので、自己選択制約式(誘因両立制約式)という。
YバーがYb*より下がれば、Bが給付を受け取るためには、少し労働時間を減らさなければならない。
そこだけ見れば、それはBにとって最適ではないように見えるかもしれない。
しかし、情報の非対称性が存在する世界では、基準となる所得制限Yバーをあえて少しを下げてやった方が、
その分Aが偽らずに働くインセンティブ(誘因)を持つようになり、
その結果、税収も増えるので、かえってBにとっても厚生を高められるのである。
Yバー=Yb*と設定したときには、A=Gとなっているので、1式が等号で結ばれる(Uaハット=Ua)。
Yバー<Yb*と設定したときには、1式が強い不等号(Uaハット<Ua)になる。
図10-7の縦軸上の記号で言えば、Ua’<Ua*となる。
1式の自己選択制約式が、前者ではもうギチギチの一杯だが、
後者は緩んでいるので、その分だけ課税Tを増やしてもAは偽らずに働き続ける。
タギングの方法2:現物給付
仮定1’:効用関数の異質性。方法1の仮定のうち、仮定1を変えて、効用関数は違うとする。
仮定2:方法1と同様に、情報の非対称性から確認できるのは所得だけ。
_ _
ここでも所得制限はY、BはY+給付Tを用いてX財を消費する。
そこで方法1のときとは違って、今度は横軸をXとする。縦軸は効用Uのまま。

図10-8では、Bの効用関数と、偽ったAの効用関数Uaハットだけを描いている。
それぞれの効用最大化水準では、Xa*ハット<Xb*となるとしよう。
Aについては、偽ったときだけを描いているのでハットも付く。
能力の低いBの方がたくさん消費するような財の例として、低質な住宅などを想定してみると分かりやすい。
_
ここでTの一部を現金ではなく、X財の現物給付としてみよう。その量をX(以下、Xバー)とすると、
給付全体のうち、現金部分はT-Xバーになる。
1:Xバー<Xa*ハットの場合
偽ってるAですら、まだXバー以上にX財を欲しいと思っているので、
現金給付部分を使ってさらにX財を購入しようとする。
このようなXバーの設定は、両者に何の影響も与えない。
2:Xa*ハット<Xバー<Xb*の場合
この領域では、偽ってるAの効用関数Uaハットは右下がり、Bの効用関数は右上がりとなるので、
Xバーの設定をこの領域になるように上げてやると、偽ってるAの効用は下げつつ、Bの効用は上がる。
3:Xb*<Xバーの場合
一見すると、Xバーの設定をBの効用最大化水準「以上」にしてしまってるので、
Bの効用を下げちゃうので良くないように思える。
しかし方法1のときと同じように、Bの効用減は微小に過ぎない一方、Aの効用減はかなり大きい。
描いてはいないが、もし偽っていないときの真のAの効用最大化水準Ua*(*は付くけどハットは付かない)
と比べて、Aの効用水準が大幅に下がってしまうぐらいまでXバーの設定を上げてやれば、
Aは自己選択制約によって自ら偽らなくなる。
すなわち、Bにとって最適となる以上に現物給付すると、
Aが不正受給をせずにちゃんと働いて税金を払うようになり、給付が本当に必要なBにとっても望ましい。
タギングの方法3:さらに所得も確認できないとき。
方法2では、Xバーという設定が出てきたが、相変わらず所得制限Yバーを基準として先に用いている。
従って、Aが不正受給するためには、労働時間を減らして所得を低く偽る必要があった。
ところが、所得獲得能力はだけじゃなく、所得水準も確認できない場合、
所得制限の設定を用いた不正受給が防止できない。
このケースも、給付の一部を現物給付とするのが効果的となる。しかもその現物給付は、必ず消費しなければならない。
住宅サービスを例に取り、低質住宅が下級財(所得が増えるとかえって消費量が減る財)であるとしよう。
高所得者が不正受給しても、低質住宅に住まなければならない場合、かえって効用は低下するので、
これまでの議論と同様に、不正受給を自らやめる。
しかも、住宅をさらに低質にすれば、より多くの不正受給者を締め出すことができる。
本来、給付を受け取るべき能力の低い人達にとっても効用は下がるが、その下がり方は小さいので、
トータルではかえって厚生が高まる。
P313の上から6行目、「方法1の場合、所得制限が余暇消費を制限している」という文章の意味について。
最初に読んだときは意味がわからなかったが、
方法1の場合、所得制限をさらに下げていけば、Aが偽って働かない(余暇を消費する)ことの効用減は大きく、
余暇消費を制限する=働かせるという意味。
・ 10章5節、利他主義。
意外と面白かった。というのも、利他主義であってもそれが複数いると問題が発生する。
・高所得者をA、低所得者をCとし、高所得者だけ利他主義とする。
・Aの効用関数は、Ua=U(Xa,Uc)
・Cの効用関数は、Uc=U(Xc)
・代入すると、Ua=U(Xa,U(Xc))となるので、結局、変数XaとXcの関数として、U(Xa,Xc)と表現できる。
すなわち、Xa-Xc平面に無差別曲線が描ける。
無差別曲線と来れば予算制約線なので、
・単純化してCの所得はゼロ
・Aからの移転所得をga
・Cの消費は、ga=Xc
・Aの予算制約式は、Ya=Xa+ga=Xa+Xc
この時点ではまだ問題ではない。問題が発生するのはここからで、もう1人の高所得な利他主義者Bがいると、
・Bの効用関数は、Ub=U(Xb,Xc)
・Bからの移転所得をgb
・Cの消費は、ga+gb=Xc
Cの予算制約式を、AとBのそれぞれの効用関数に代入すると、
・Ua=U(Xa,ga+gb)
・Ub=U(Xb,ga+gb)
・ga+gb=Xc
これはもはや、公共財の(相対)価格が、p=1のときの自発的供給(拠出均衡)の問題と同じ構造となる。
AとBはお互いに相手が出してくれることを期待してフリーライダーとなり、
パレート非効率的な水準となる(過少供給となる)。
従って、AもBも利他主義者にも関わらず、公的部門の介入がパレート改善に必要となる(本当にジレンマだな)。
また拠出均衡と同じ5章4節のクラウディングアウトで説明したように、
定額の固定税で政府が所得移転すると、同額だけAとBは自身の所得移転を減らす。
課税を定率にして、所得移転は定率補助にする必要がある。
・ 10章6節、サマリア人のジレンマ(サマリアびと、と読むらしい)。
そもそも10章は全体として、公的扶助とその効率性を分析する章である。
そこで6節では、動学的不整合性を検討する。
すなわち、公的部門が効率性を考えて、困窮者にできる限り自助努力をさせたくて、
困ってても助けないと宣言しても、その助けないという約束に法的拘束力や強制・義務がない限りは、
実際に困窮者が発生すれば、やっぱり助けた方が公的部門にとっても厚生が高い。
従って、困窮者はどうせ助けてくれるだろうと期待して、自助努力を行わない。
そのような口約束は、ゲーム理論的に言えば、部分ゲーム完全均衡ではなく、
信憑性のない脅し・コミット(宣言)となる。
動学的不整合性とは、事前に最適である戦略が、事後的には最適ではなくなること。
貯蓄と年金がいい例で、老年期に所得が無くて困るようなら、若年期に貯蓄しておいて欲しいと思って、
公的部門が老年期の困窮者は助けないと宣言しても、そのような戦略は公的部門にとって事後的に最適ではない。
それを見込んだ人々は、必ず救済されると期待して、若年期に貯蓄するより散財してしまうことになる。
このような動学的不整合性の対処法として、法的拘束力のあるコミットや、法的な強制・義務である。
貯蓄の例で言えば、強制的に社会保険料を徴収し、強制的に貯蓄させる年金制度、
義務教育の必要性も同じ理由となる。
保険というのは、加入者が多くなるほど大数の法則が生かせる。
規模の経済みたいなもので、母集団の期待値(母平均)と、標本平均が、完全に一致する。
ただしこの理由だけでは、別に民間の保険がダメで、社会保険でなければならない理由にはならないが、
他に根拠として、民間の保険だと逆選択が発生すること。全員が強制加入だと逆選択は起きない。
ただし、逆選択の方はそれで解消できても、モラルハザードの問題は、民間の保険と同様に社会保険でも起きる。
民間の保険でもよく用いられているモラルハザードを防ぐ制度として、完全保険にしないこと。
完全保険とは、事故・病気・火災などの損害が、起きても・起きなくても、所得水準が同じになるような保険。
損失が完全にカバーされているという意味だろう。
ちなみに、公正な保険というのは、保険会社の利潤が(参入により)0となるような保険。
完全保険にしないってことは、何か損害が発生しても、被保険者に一定額を必ず負担させるということ。
医療保険の自己負担制度とか。完全に保険で無料だと、やはり医療サービスの消費は過大となる。
1000円でも自己負担があれば、過剰消費を減らせるだろう。
他にも免責条項を設定して、被保険者がそれに違反するような危険な行動を取れば保険金が減少したり、
逆に一定期間無事故であれば保険料を下げるなどの制度もある。
○ 12章3節、年金。
年金保険とは、所得が得られなくなる老後において、予想よりも長生きしてしまった人と、
早く死んでしまった人の間での再分配を通じた、リスクをシェアする機能。
ただし、民間保険には逆選択の問題があり、老後のための貯蓄(自己保険)には、
政府の救済を期待した動学的不整合性の問題がある。
強制加入の社会保険(公的年金保険)は、両方の問題を解決できるが、モラルハザードの問題もある。
モラルハザードの問題はちょっと置いておいて、本節では世代重複モデル(OLGモデル)で、
年金制度の比較を行ってみよう。代表的個人モデルと違って、家計は一定期間後に死ぬモデル。
・登場する経済主体は、死なない政府と企業。一方で、t期に生まれてt+1期に死ぬ家計(2期間OLG)。
・政府は公的年金の運営のみ。それ以外の政府活動は行わない。
・家計は若年世代(t期)に賃金所得(wt)を得て、老年世代(t+1期)では自分の貯蓄と年金だけで生活。
・払うのが保険料、もらうのが保険金(以下、給付金とする)。加入者を被保険者、運営する側を保険者。
・t期の所得にかかる保険料率=τt
・t+1期の若年世代の所得wt+1に対して、t+1期の老年世代が受け取る給付金の比率=所得代替率(st+1)。
このように記号を定義すれば、t+1期の給付金は逆に次のように表現できる。
t+1期の給付金/wt+1=st+1 → t+1期の給付金=st+1・wt+1
・t期に生まれた世代の、t期における消費=c1t、t+1期における消費=c2t
・t期の若年世代が、次期に持ち越す資産(すなわち自分で行うt期の貯蓄)=at+1(t+1という表記に注意)。
運用先は企業への投資と、公債の購入。
c1t=(1-τt)wt-at+1 ・・・1
c2t=(1+rt+1)at+1+st+1・wt+1 ・・・2
教科書とは式番号を変えるので注意。式番号を振ってなかったり、番号が大きくて重たいので。
1式のat+1を2式に代入すると、2期間モデルでよく見る家計の予算制約式、
c2t st+1・wt+1
c1t + ────── = wt - (τt・wt - ───────) ・・・3
1+rt+1 1+rt+1
3式右辺の第2項(括弧全体)は、政府に対する家計のネットの支払い(純支払い)の割引現在価値。
つまり、支払いと受け取りの差額の割引現在価値で、それをTと表記すると、t期のTは、
st+1・wt+1
Tt=τt・wt-─────── ・・・4
1+rt+1
企業がt+1期に利用できる資本ストックは、家計のat+1だけではなく、
政府が資産を持って運用する資産もある(at+1はすでに税引き後なので)。
政府は公的年金以外に活動していないので、運用するなら企業しかないからである。
その政府の持ち越す資産がマイナスなら、借金していることを意味し、公債が発行される。
企業の投資から得られる利子率より、公債の利子率が低いと、家計に公債を買ってもらえない一方、
わざわざ高くする必要もないので、公債の利子率と企業への投資で得られる利子率は、rt+1で等しい。
t期に発行された公債は、もし公債の中立命題(リカード=バローの等価定理)が成り立つのなら、
t期の若年世代は、公債償還=増税に備えて、その分貯蓄する。
OLGモデルなので、t+1期では老年世代となっていて働いていないので、所得税を払う心配はなく、
t+1期には死ぬのだが、増税のタイミングがt+1期以降であったとしても、
利他的遺産動機があれば、中立命題は成り立つ(本書のP353を参照)。
しかしここでは、中立命題は成り立たないと仮定して、t期に発行された公債は、
t期の若年世代の増税につながらなければ、家計はat+1(すなわち貯蓄)を増やさないとする。
政府がt期に公債を発行して得た歳入は、t期の公的年金保険の給付に使われるのならば、
t期の老年世代の消費に使われるだけとなる(後述の賦課方式のケース)。
たぶん本書では、わざわざ借金してまで政府が企業へ投資を行うことはないという想定なのだろうと思うが、
以上の設定により、経済全体で企業が利用できる資本ストックは、at+1から公債を差し引いたものとなる。
すなわち、公債の発行(=即給付の一方で貯蓄は増えない)によってクラウディング・アウトが起きることになる。
もし中立命題が成り立っていれば、たとえ完全雇用が成立していても、
公債の発行+減税(や給付)は、同額の貯蓄が発生するので、クラウディングアウトは起きない。
(もしくは、後述の積み立て方式の場合には、クラウディングアウトは起きない。)
あるいは不完全雇用+金融緩和がセットならば、公債発行+公共投資でもクラウディングアウトは起きない。
例えば、10兆円の公共投資が行われれば、乗数過程において必ず10兆円の貯蓄も発生する。
・中立命題○ならば、限界消費性向c=0。公共投資で国民が受け取った所得10兆円は、そのまま全額貯蓄される。
ただし、均衡予算乗数=1なので、GDPは増える。
・中立命題×でc>0、例えば0.6としよう。10兆円の所得が発生すれば、4兆円の貯蓄+6兆円の消費、
さらに6兆円の所得発生から、2.4兆円の貯蓄+3.6兆円の消費、
さらに3.6兆円の所得発生から・・・・と計算していけば、
乗数過程で発生している貯蓄を合計すると、ちゃんと10兆円になる。
Y=C+Gで、C=cYを代入すると、Y=G/(1-c)。
公債発行で賄うので租税Tを無視すると、S=Y-C、S=Y-cY=(1-c)Y=G。
・ 財政方式と給付方式
財政方式:2種類あって、賦課方式と積立方式。
給付方式:2種類あって、確定給付と確定拠出(後者は、被保険者が運用リスクを負う。)
本書ではリスクの問題は扱わないので、給付方式の違いは区別しない。
財政方式で問題となるのが、政府の予算制約式。
・ 賦課方式では、積立金も公債発行もない。t期の人口をNtとすると、
賦課方式での予算式:Nt・st+1・wt+1=Nt+1・τt+1・wt+1 ・・・ 5A
t期に生まれた世代は、右辺のt+1期の若年世代が支払った保険料を、給付してもらう。
Ntは、Nt+1と、等しいとは限らないので、wt+1に対する比率を表すst+1は、τt+1と等しいとは限らない。
・ 積立方式では、政府に積立金があり、それを政府が運用しているので、
積立方式での予算式:Nt・st+1・wt+1=Nt・τt・wt・(1+rt+1) ・・・6A
t期に生まれた世代は、右辺のt期で支払った自分の保険料を、rt+1で運用してもらって給付を受け取る。
支払いも受け取りも、どちらも自分なので、両辺ともNtである。t+1期の世代は出てこない。
ただし、左辺には相変わらず、wt+1が出てくる。
st+1の定義が、t期の老年世代が受け取る給付金の、t+1期の若年世代の賃金wt+1に対する比率だからだ。
・ τt=τと一定にした上で、両方式の違いを見てみる。予算式5A式を踏まえた上で、まずは賦課方式から。
Nt+1・τ
Nt・st+1・wt+1=Nt+1・τt+1・wt+1 → st+1=────── ・・・5B
Nt
t期の若年世代のネットの支払いである4式に、5B式を代入すると、
st+1・wt+1 Nt+1 wt+1 τwt
Tt=τt・wt-───────=(1+rt+1 - ───・────)・───── ・・・7A
1+rt+1 Nt wt 1+rt+1
7A式の右辺の括弧の中が、マイナスだった場合、右辺全体でマイナスとなるから、左辺もマイナスとなる。
Ttは割引現在価値で見たネットの支払なので、それがマイナスということは、受け取り超過を意味する。
Nt+1 wt+1
───・──── > 1+rt+1 ・・・8A
Nt wt
ここで次のような記号を準備する。
Nt+1-Nt Nt+1 Nt+1
人口成長率:──────=───-1=nt+1 → 1+nt+1=─── ・・・9A
Nt Nt Nt
wt+1
賃金成長率:1+γt+1=─── ・・・9B
wt
8A式に、9A式と9B式を代入すると、
(1+nt+1)(1+γt+1)=1+nt+1+γt+1+nt+1・γt+1 > 1+rt+1 ・・・8B
nt+1とγt+1はゼロに近い数字なので、その積の項(nt+1・γt+1)は無視できるとすると、
nt+1+γt+1 > rt+1 → 人口成長率+賃金成長率 > 利子率 ・・・8C
8A式が成立していれば、賦課方式のおかげで払った以上にもらえる。
その原資は次の世代の所得からなので、世代間再分配が行われていると言える。
・ τt=τと一定にした上で、予算式6A式を踏まえた、積立方式について。
st+1・wt+1
Nt・st+1・wt+1=Nt・τt・wt・(1+rt+1) → ───────=τt・wt ・・・6B
1+rt+1
t期の若年世代のネットの支払いである4式に、6B式を代入すると、
st+1・wt+1
Tt=τt・wt-───────=τt・wt-τt・wt=0 ・・・7B
1+rt+1
(P367の同式では、中央の辺の2項目の分子は、st+1だけになっているが、誤植だと思う。)
人口成長率も賃金成長率も関係ないので、世代間再分配は生じない。
家計は同質で、かつ、リスクの問題は捨象しており、政府の運用も同じ市場利子率なので、
積立方式は家計の貯蓄と完全に代替的である。
というのも、まず年金制度がない場合の予算制約式を考えてみると、1式~3式を見ればわかるように、
保険料率のτtや、給付金のst+1・wt+1がない。
一方、積立方式の7B式より、3式の2項目が無くなるので、
積立方式の下での家計の予算制約は、年金制度が無いときと完全に同じになるからだ。
積立方式であれ賦課方式であれ、年金制度が存在している時点で、t+1期で給付がもらえることは確かで、
どちらの方式だろうと、家計のt期の予算制約より、at+1は必ず次のようになる。
c1t=(1-τt)wt-at+1 → at+1=wt-τt・wt-c1t ・・・1
従って、τt・wtの分だけ必ずat+1が減少することは間違いない。
賦課方式の場合に問題なのは、Tt≠0なので、所得効果も追加的に生じて、c1tが変化し、at+1もさらに変化する。
資本ストックの量が変化すれば、wtも変化するので、その経路の効果も発生するだろう。
積立方式の場合、Tt=0なので、その効果は生じない。
ただし、P367では、両方式でat+1が減ることをもって、一種のクラウディングアウトと呼べると言っているが、
企業が利用できる資本ストックが減少するかどうかという意味では、賦課方式の場合は上記のようにありうる。
賦課方式の場合、確かに公債は発行しない。しかし、徴収した保険料の運用もしない(資産を持たない)。
t期の若年世代が支払ったτt・wtは、政府に積み立てられて運用(企業向け)されるのではなく、
t期の老年世代にそのまま給付され、同じt期に即座に消費される。
一方、t期の若年世代は、t+1期に給付がもらえることをあてにして、at+1は減らすからだ。
しかし、P368でも書かれているように、積立方式の場合は、企業への投資額=資本ストックは減少しないので、
その意味でのクラウディングアウトは起きない。
年金が貯蓄を完全代替するということは、民間貯蓄が政府貯蓄という名前になるだけで、
貯蓄そのものは全体で減ってない(運用先も一緒)ので、
公的年金制度(積立方式)がある時とない時とで、企業が利用できる資本ストックの量は不変だからだ。
・ P368~P372、人口動態。
積立方式と比べて賦課方式の場合、8C式によって人口成長率と賃金成長率の影響を受ける。
人口動態の影響について考えるために、賃金成長率は一定と考えよう。
ある変数の影響を調べるときには、他の変数は一定とするのが経済学(だけじゃないが)的手法である。
nt+1が低下すれば、t+1期の老年世代にとって、年金の原資となるt+1期の若年世代の所得合計は少なくなる。
子育てに伴う色々な費用を払って来なかったと言えばそれまでだが、年金だけを見れば損をする。そこで、
t+1期の給付金/wt+1=st+1
であったことを思い出そう。なぜこのような記号をわざわざ定義したかというと、
人口成長率が変化しても、st+1=sで一定ならば、t+1期の老年世代が損をするとは限らないからだ。
(一方で、仮定により賃金成長率は不変だし。)
賦課方式の予算式5A式と、人口成長率の9A式を再掲して、ネットの支払い4式について改めて見てみると、
Nt・st+1・wt+1=Nt+1・τt+1・wt+1 ・・・ 5A
Nt+1
1+nt+1=─── ・・・9A
Nt
st=st+1=st+2=・・・=sとすれば、5A式は、1+nt+1=s/τt+1となるので、
st+2・wt+2 wt+1 wt+2
Tt+1=τt+1・wt+1 - ───────=(───── - ─────)・s ・・・7C
1+rt+2 1+nt+1 1+rt+2
人口成長率の1+nt+1が小さくなれば、t+1期における若年世代のネットの支払いは大きくなる。
これまでの分析では、τt=τで一定にしていたので、
賦課方式の下で人口成長率が変化すると、5A式で言えば、その影響はst+1に現れていた。
今度は、st+1=sで一定と考えるので、5A式で言えば、左辺全体を一定としたまま
Nt+1の減少をτt+1の上昇で相殺していることになる。
次に、積立方式の場合について。人口成長率がどうなろうと、ネットの支払いは常にゼロなので、
各世代の負担は変化しない。
・ わからないことを、正直に告白。
P369の一番下の行~P372の、賦課方式から積立方式への移行と世代間負担の話が、
個人的にまったく分からない。
t期に移行するとして、t-1期の若年世代が払った保険料は、t-1期の老年世代にすでに支給されている。
t期の若年世代は、t-1期の若年世代(t期の老年世代)に、保険金を支払いつつ、
自身がt+1期で保険金をもらうために、積立金も払わなければならない。
移行期であるt期に負担が集中し、2重の負担と言われる。
t期以降のすべての世代に公平に負担してもらうために、
永久公債を発行しつつ、(永久公債なのに)償還していくとする。
人口N、賃金率w、利子率rを一定とし、償還財源も労働所得税として、すべての世代に公平にτとする。
(なんか同じ記号だけど、積立制度の年金保険料のτとは別に、追加で払っていることになると思う。)
t期以降が負担した税の、割引現在価値の合計は、無限等比級数の公式より、
Nτw Nτw 1+r
Nτw+────+──────+・・・=────Nτw
1+r (1+r)^2 r
ここまでは分かる。理解できないのはここからで、なぜかP370の下から5行目で、
移行期であるt期の老年世代に支払う保険金を、Nsと言っている。もう1度書くが、
t+1期の給付金/wt+1=st+1 なので、Nswじゃないのかな?
そこで、次のサポートウェブの正誤表を見てみると、
http://yuhikaku-nibu.txt-nifty.com/blog/2010/10/post-d373.html
[誤]これが移行時点での引退世代への年金給付Nsに等しいから
[正]sを1人当たり給付額と読み替えると,これが移行時点での引退世代への年金給付Nsに等しいから
とのことらしいが、それでも分からないw
結果、下から4行目で、
r
τw=────s
1+r
と書いてあるけど、忘れている設定や記号があるのかと何度も読み返したが、分からない。
左辺はτだけじゃないのかな?
さらに、P372の1行目で、12-13式(本ノートでは、7A式)に、
Nt+1=Nt、wt+1=wt、rt+1=rt、を代入するというのは分かる。
ところが、最後にτwt=sを代入して、
r
T=────s
1+r
となるから、移行後の世代の負担は、賦課方式を存続させたときと比べて変化しない。
と言っている。???である。
同じ記号τを使っているけど、賦課方式のままなら、本来なら追加で負担は発生しないはずなので、
変化しないというのはありえないと思うんだけど、自分が間違っているとしたらどこなのかも分からない。
そもそも、τwt=sを代入というのが突然出てくるのだが、なぜなのか・どういう意味なのかまったく分からない。
何度も読み返してチャレンジしているのだが、未だに分からない。
・ 賦課方式から積立方式への移行と、「課税標準化理論」
t期に移行する場合、t-1期の若年世代はすでに保険料を支払っている。
しかしそれはt-1期の老年世代に給付されてしまっている。
t期の若年世代は、積立方式なのでt+1期で老年世代になった時のために、
t期において積立金のための保険料を支払いつつ、
t-1期生まれでt期に老年世代になっている人の保険金給付も支払わなければならない。
「二重の負担」と言われ、t期の若年世代だけが移行の負担を全部引き受けることになる。
それでは世代間で不公平だということで、発生した負担をt期以降の全世代に、
平等に負担してもらおうという発想が出てくる。
それが、「課税の標準化」と言われる概念で、本ノートではちょっと前後するが、
本書ではちゃんと12章の2節で先に説明される。
上記の年金制度移行の負担に限らず、t期の公共財の供給費用の負担について、
その公共財の便益がt期以降の世代にも及ぶのなら、
最初の資金調達は国債発行で調達して、その国債の償還は各世代でまんべんなくという発想だ。
・ 12章4節、世代間の公平性。短いが素晴らしい文章だと思う。
それでも全部書き写すのはしんどいので、要点をまとめると、
・世代間の所得移転により、支払っている世代を損、受け取っている世代を得、という単純化は正しいだろうか?
・基準は所得移転だけではない。技術進歩、民間の資本ストック、社会的インフラ、etc。
・技術進歩、資本蓄積、経済成長がある中では、後の世代から前の世代への所得再分配は否定しえないだろう。
(例えば、負担能力の高い先進国が後進国へと再分配することは、良いことだろう。)
・公的年金や公債発行は、どの世代に属するのかわからないというリスクをシェアする機能がある。
・教育投資や贈与・相続は、上記とは逆に、前の世代から後の世代への所得移転とも言える。
・つまり世代間の所得移転は、それだけで世代間の公平性を損なうものとは限らないということ。
・だからと言って、過度な所得移転は、それはそれで不公平である。
・特に経済成長率が低下すると、後から前への所得移転は是認されにくくなるだろう。
・経済成長が低下し始める最初の勤労世代は、賦課方式から積立方式への移行と同様に、負担が集中する。
・公平観は社会の価値判断に依存するとはいえ、負担が集中することは制度そのものへの否定につながりやすい。
・制度の時間的視野に比べて、家計のそれは短い。従って制度設計時点で参加していない可能性もある。
・価値判断の問題とはいえ、メリット・デメリットを含めた情報公開と、十分な理解と検討がまずは必要。
経済学ノートのトップページに戻る

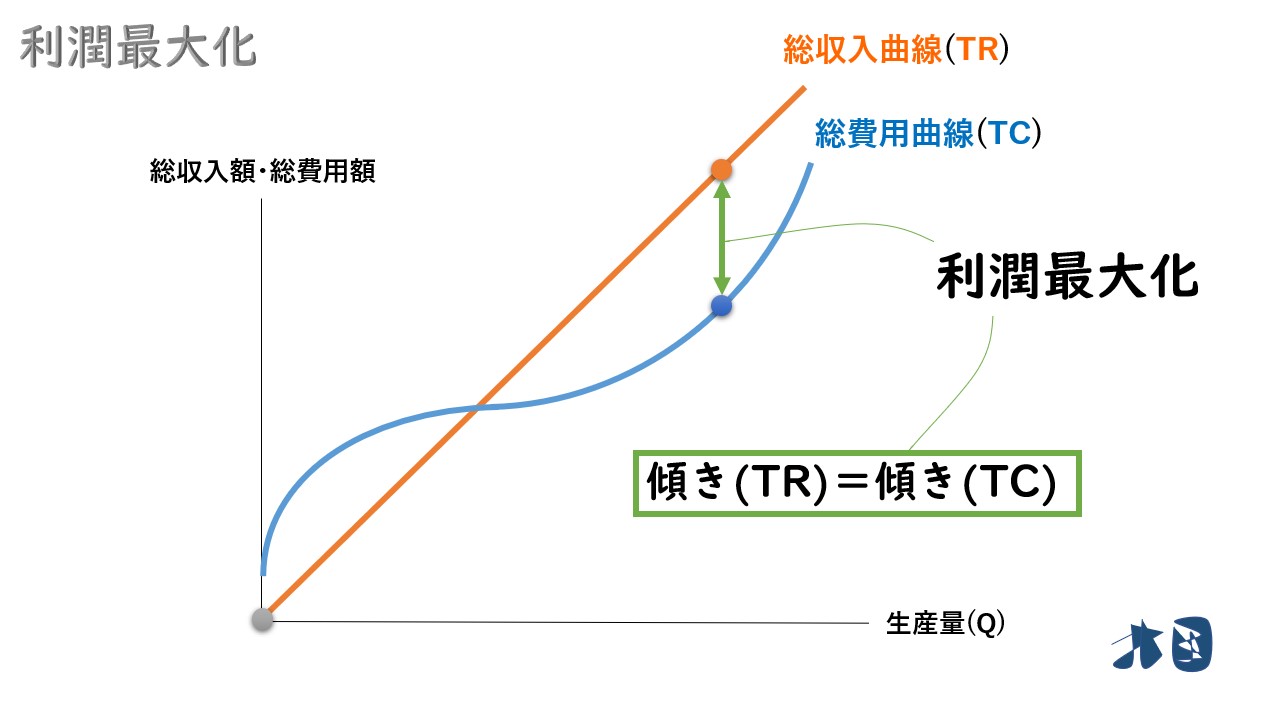

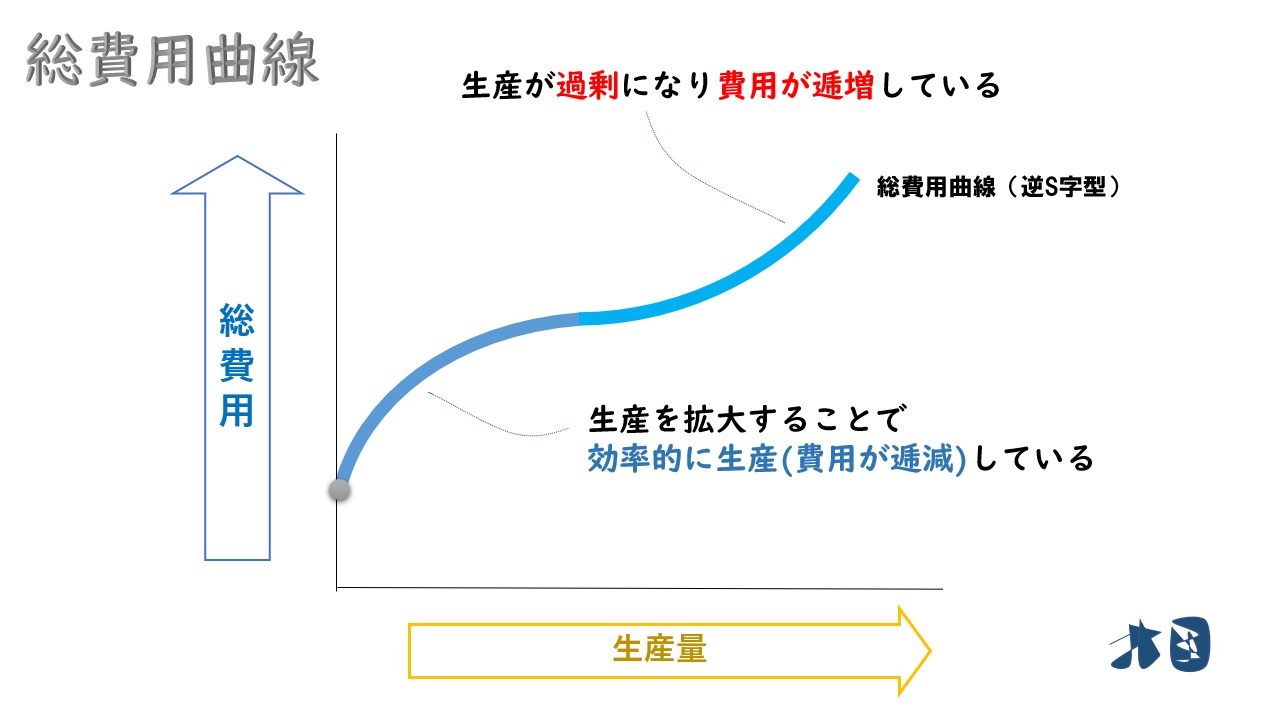
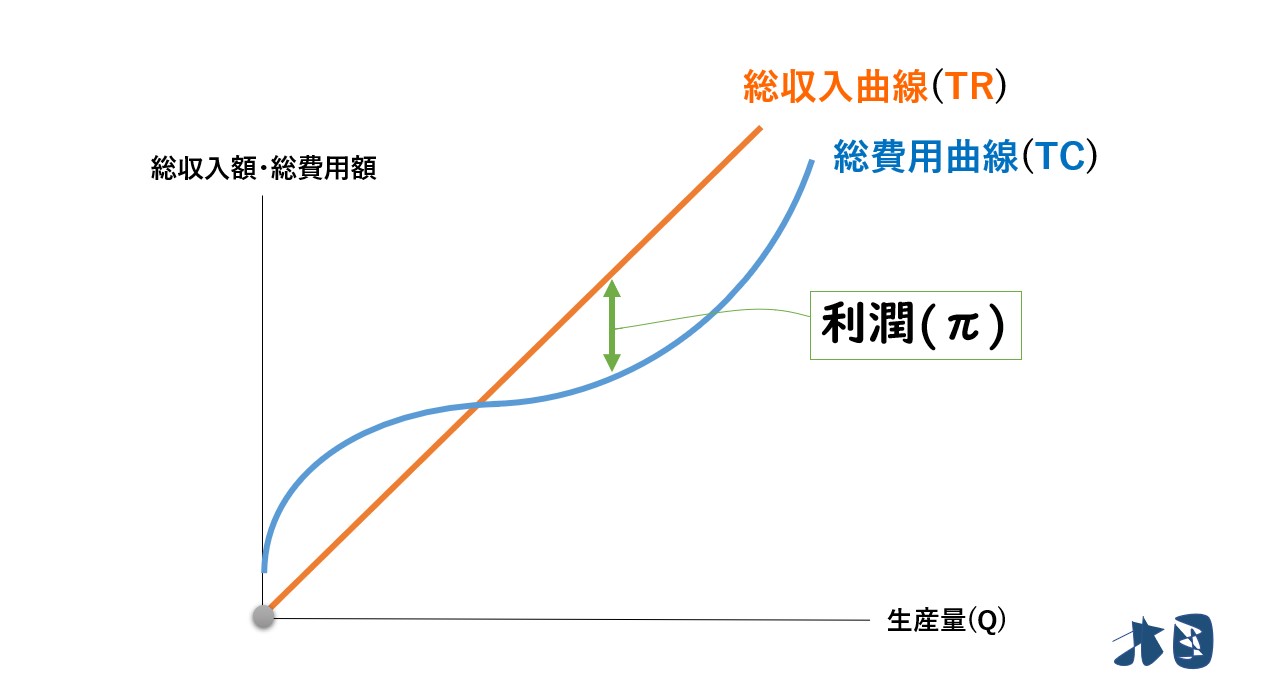

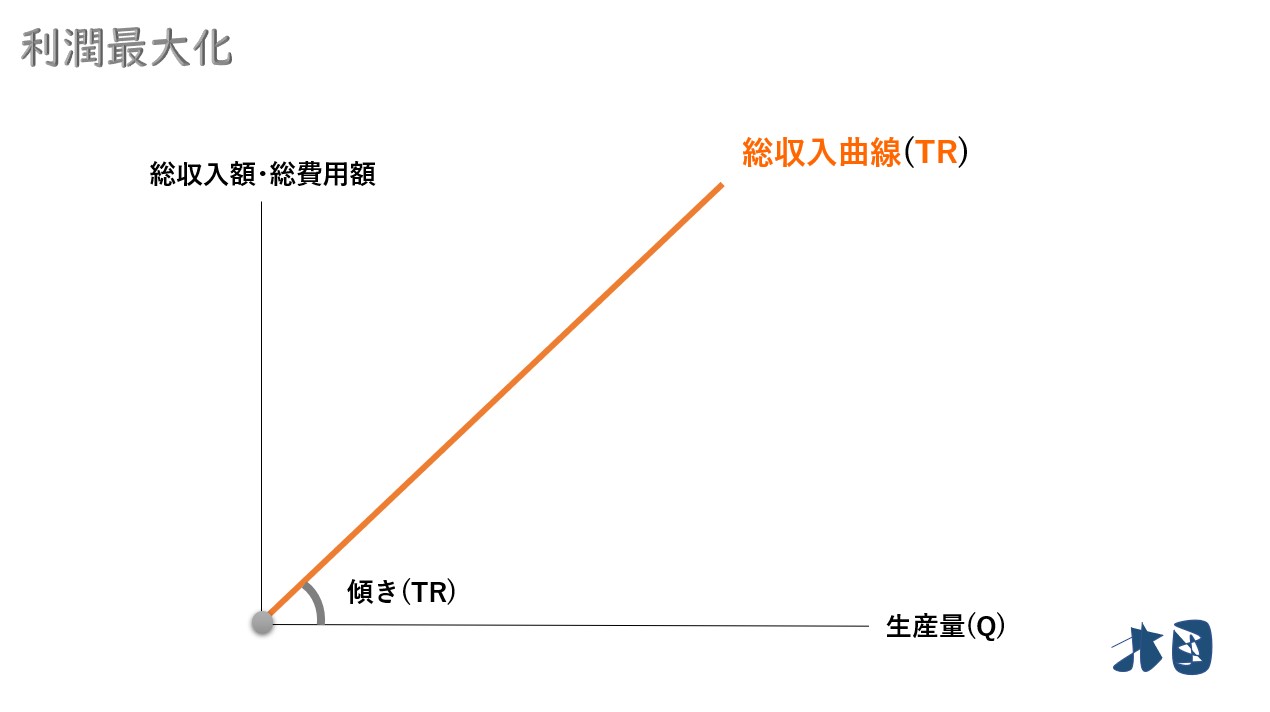
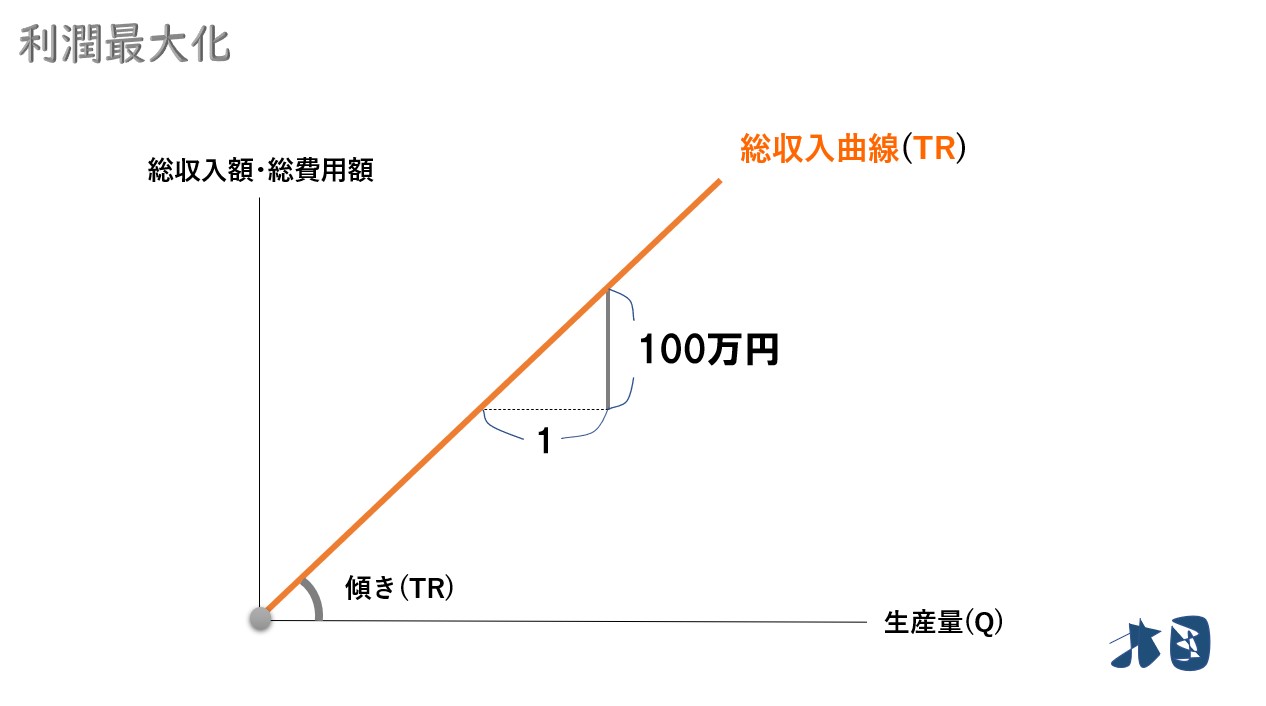
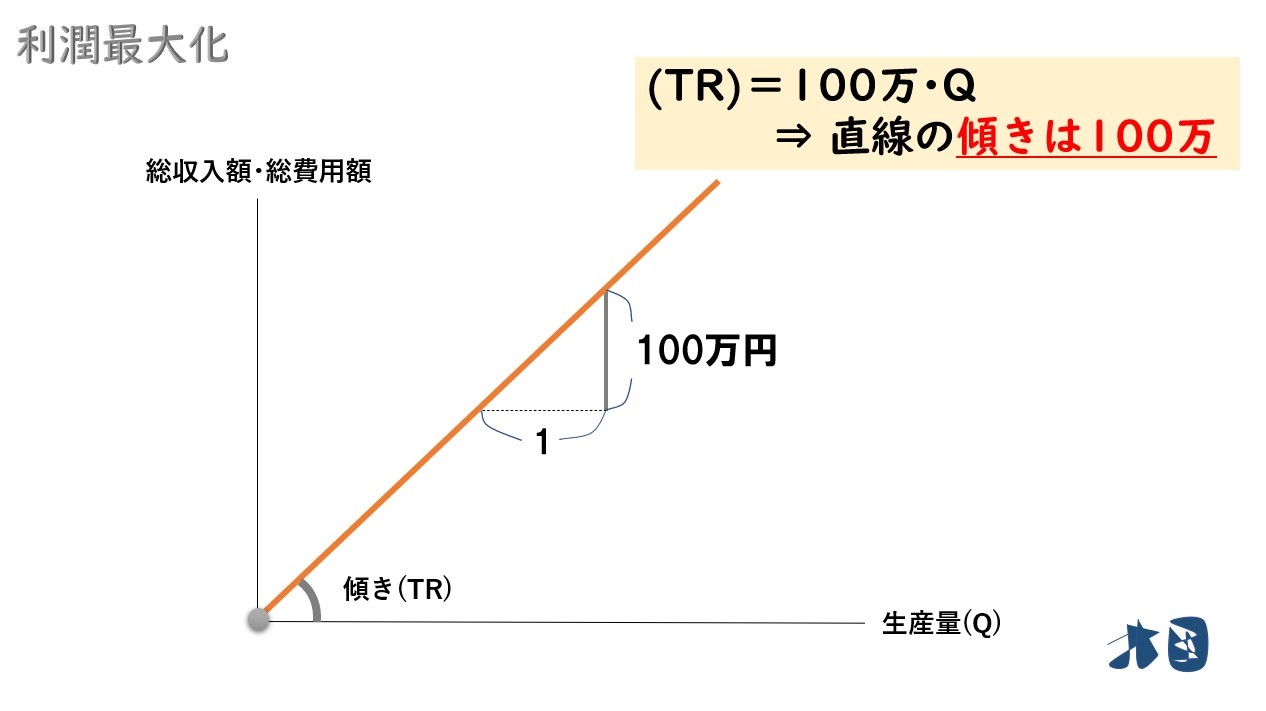
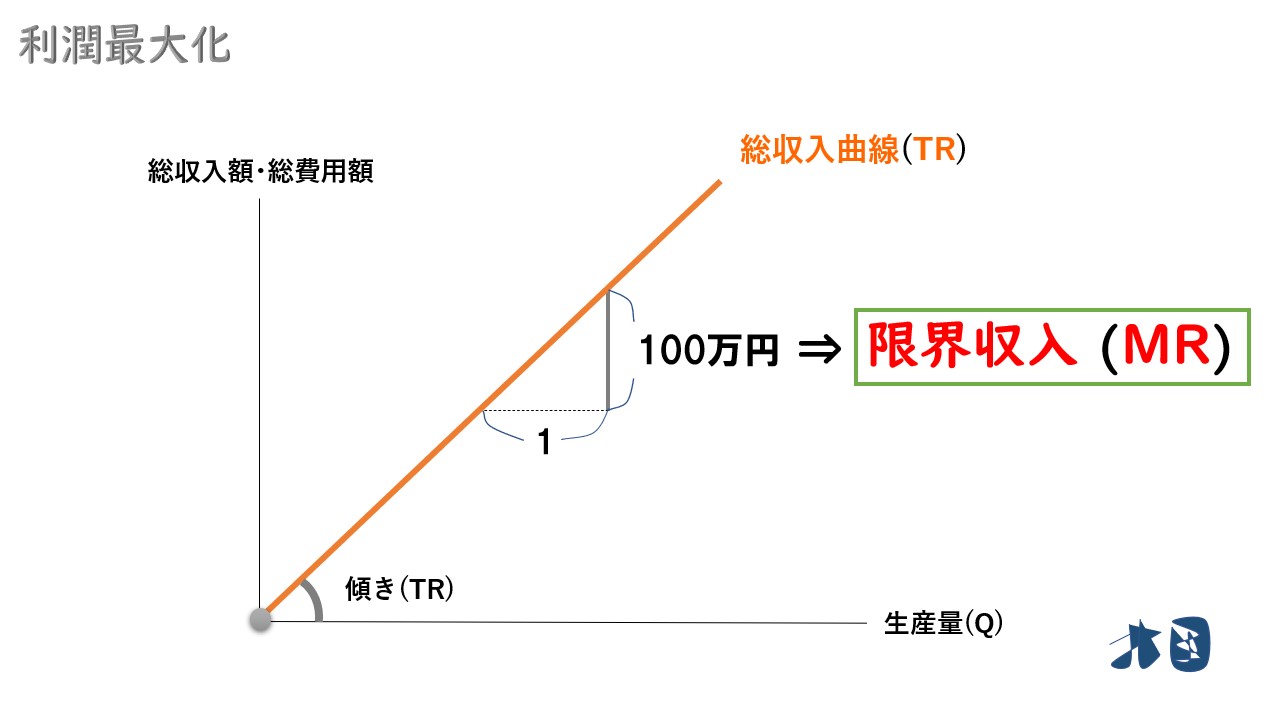
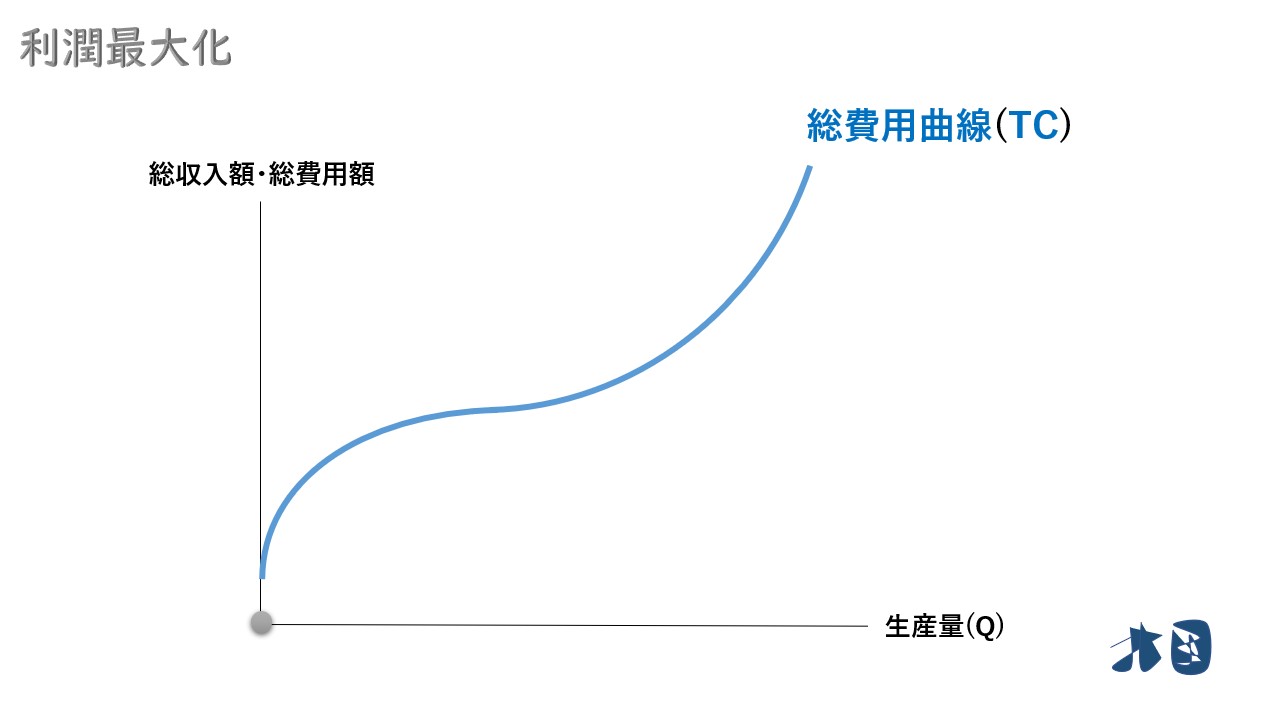
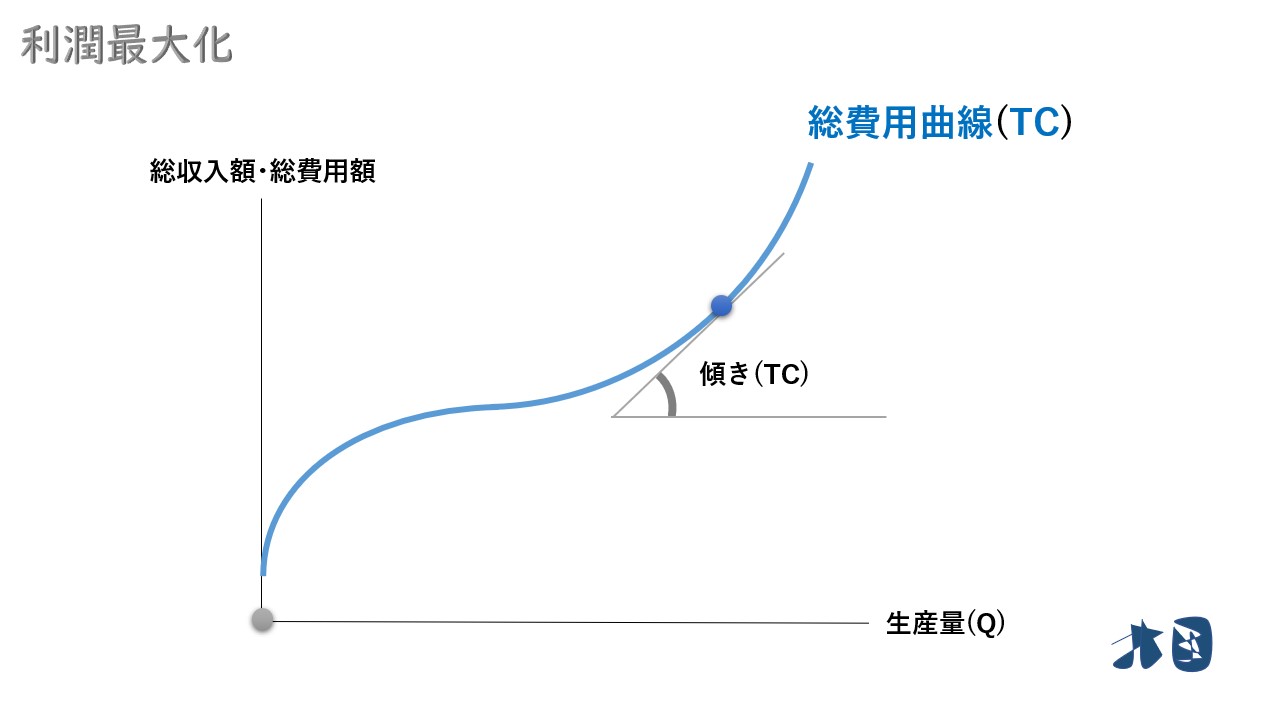
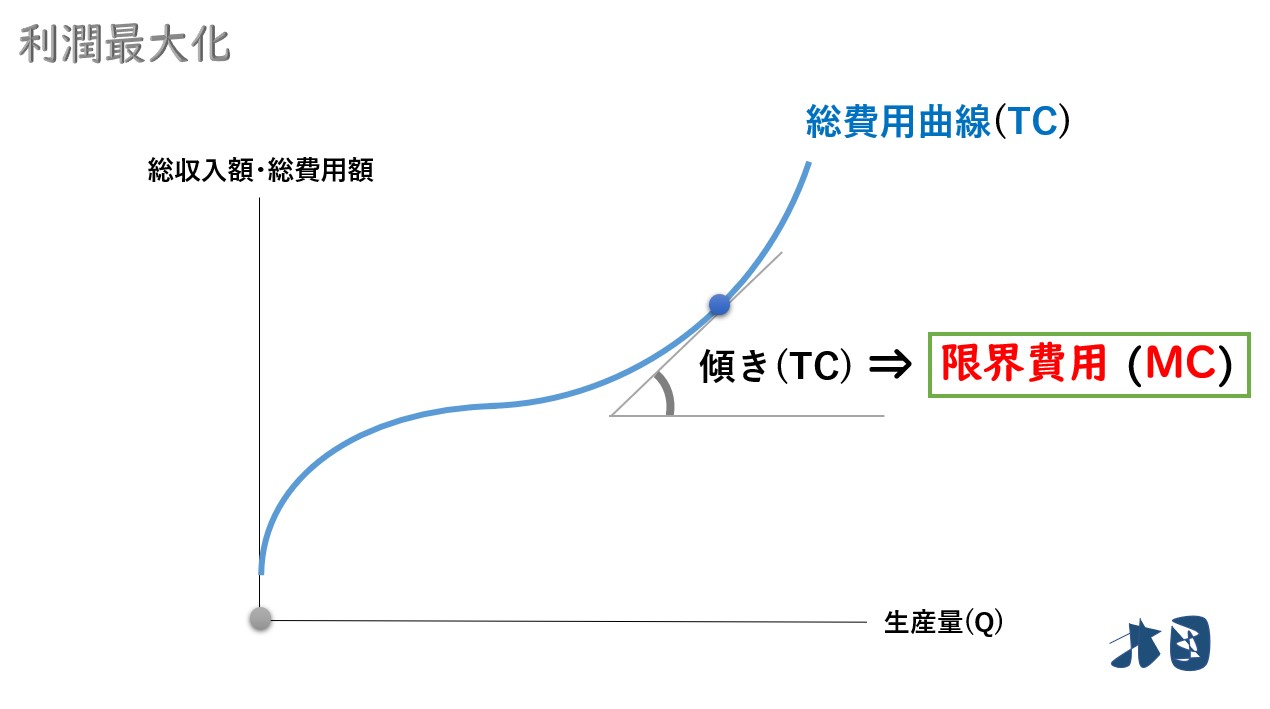
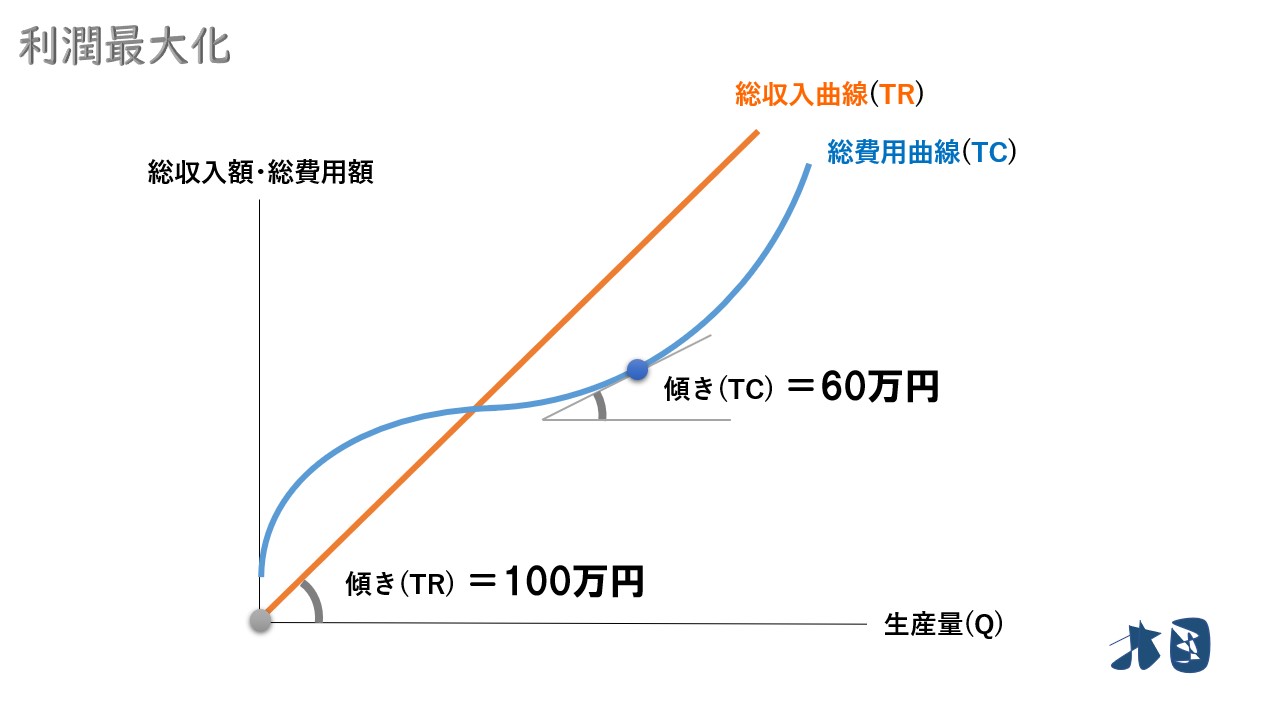
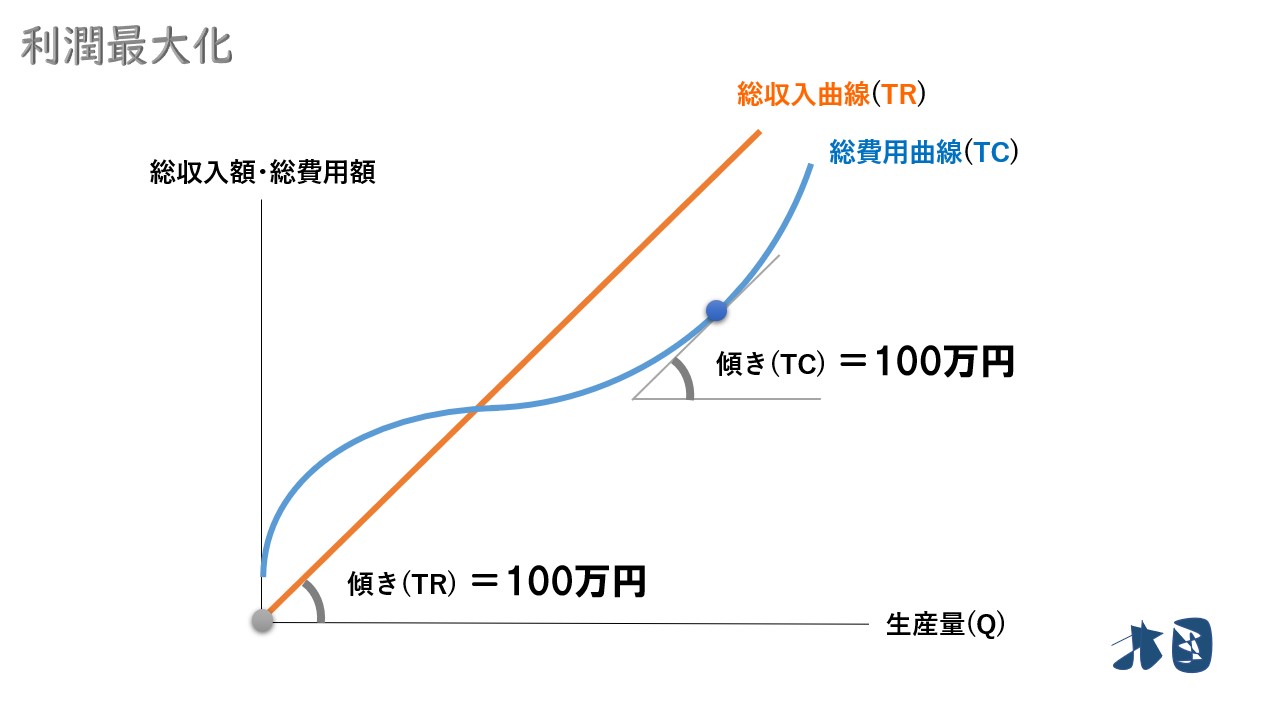

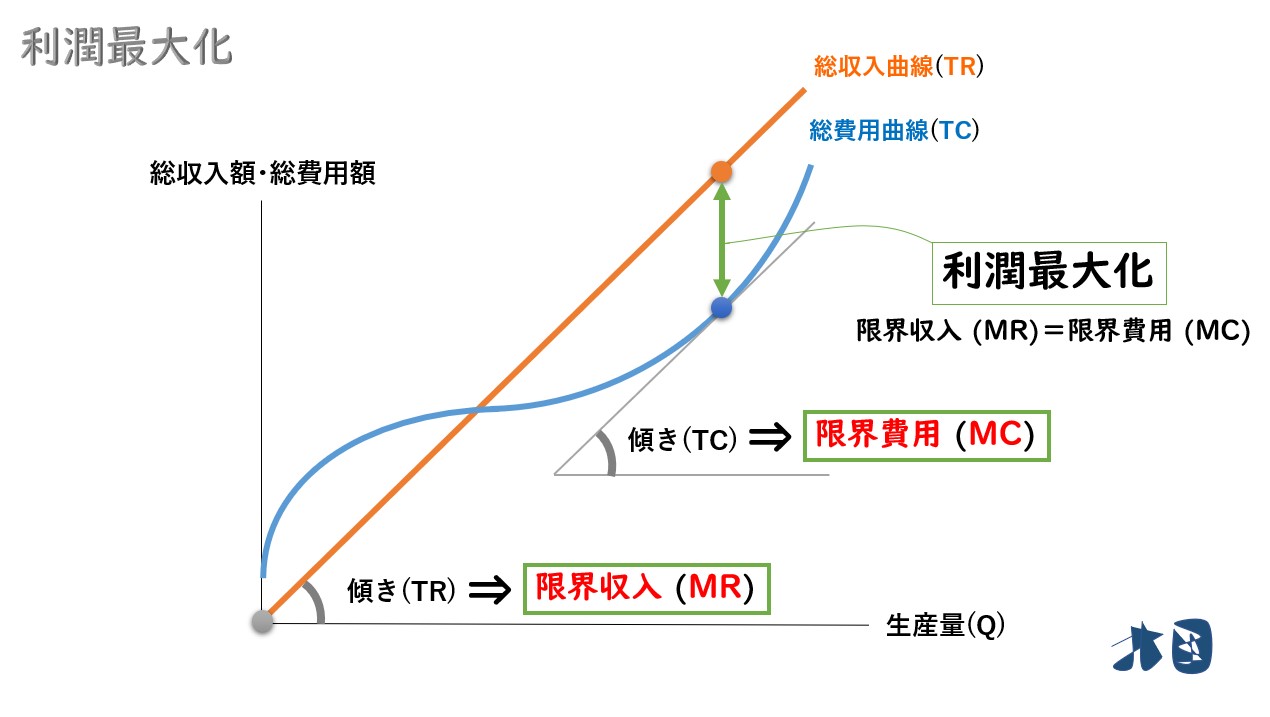

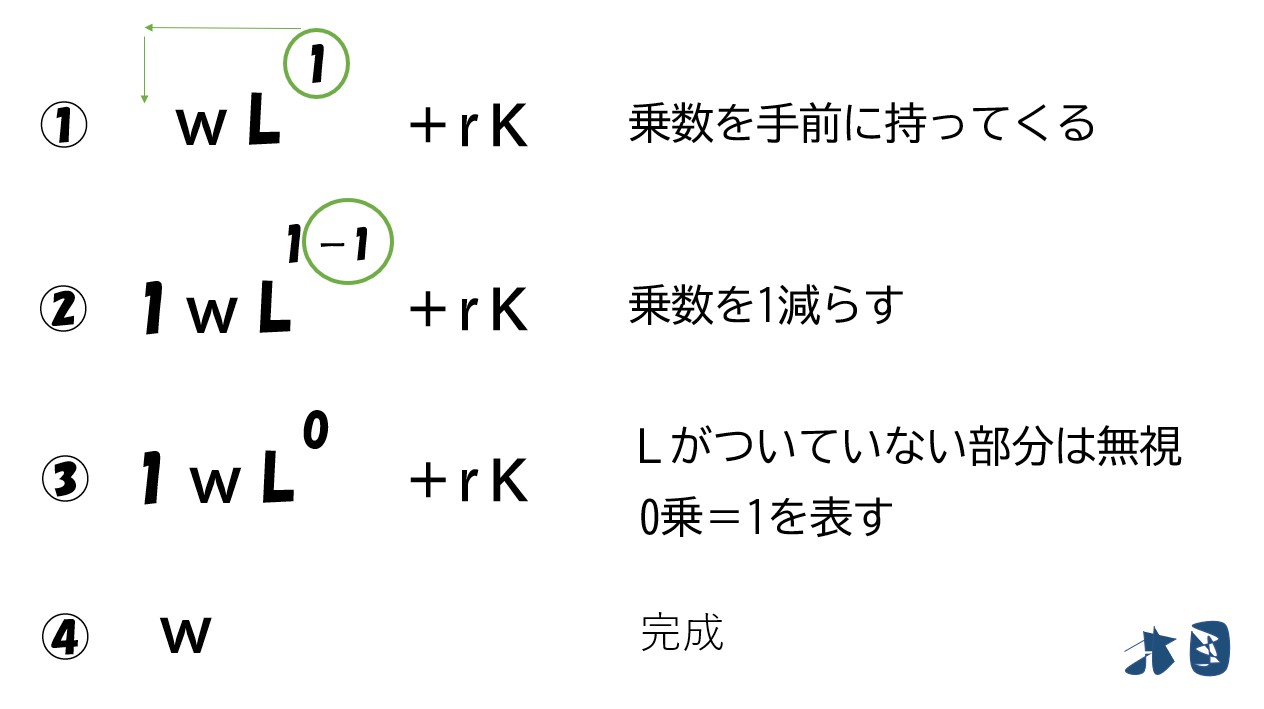

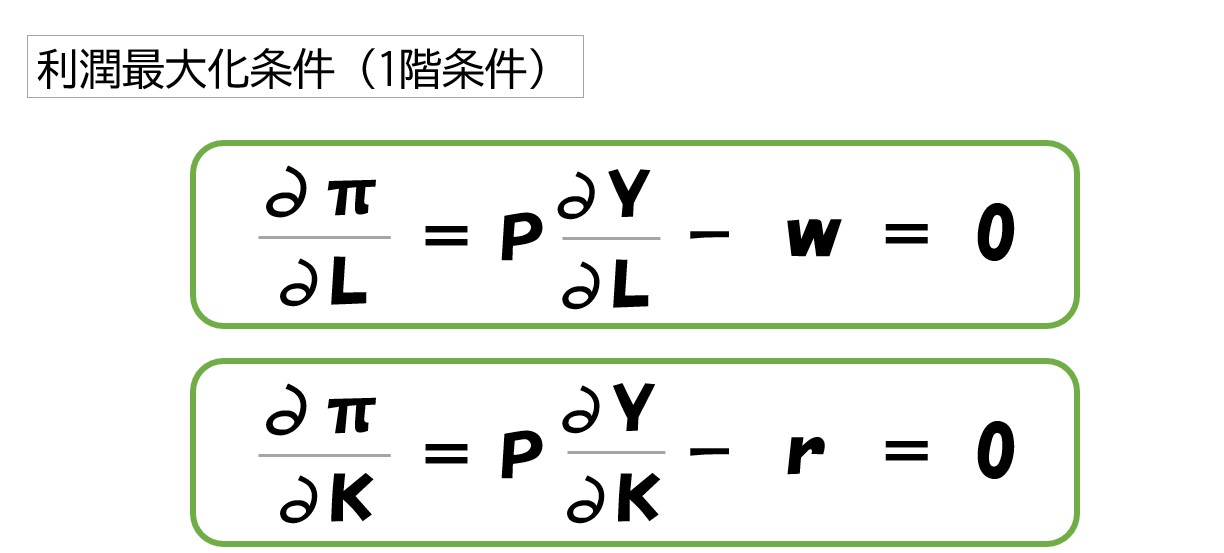

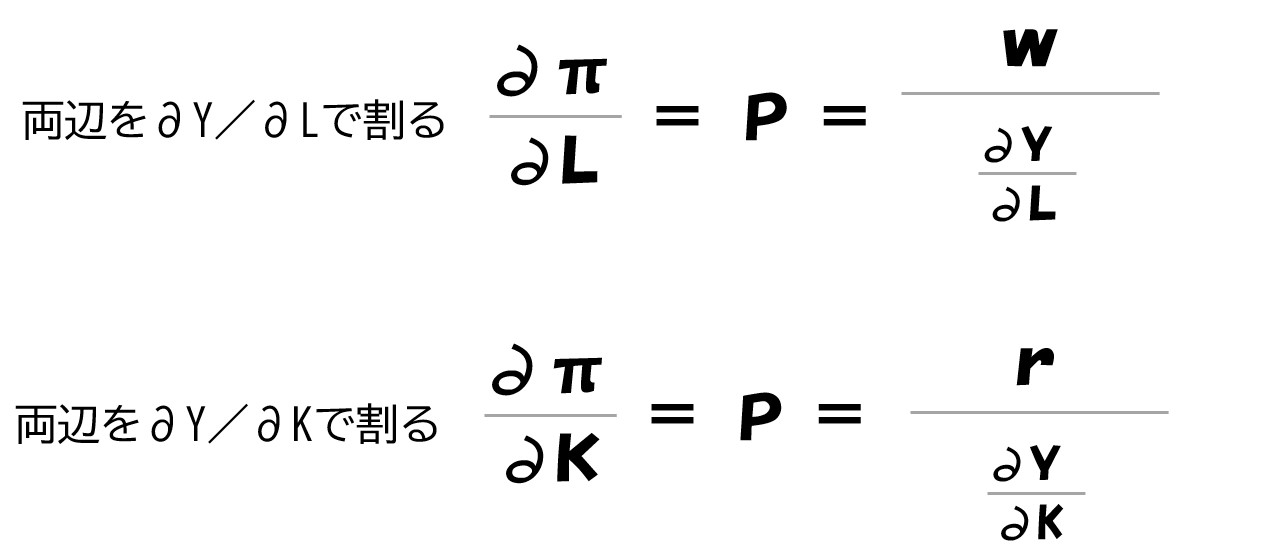
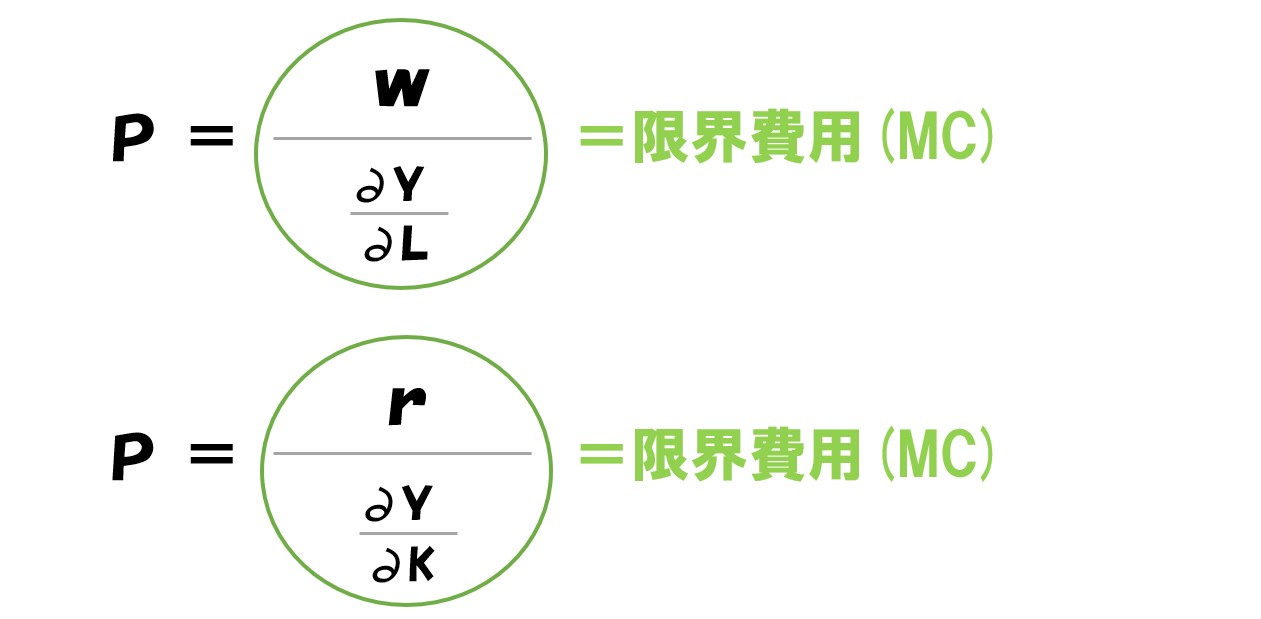
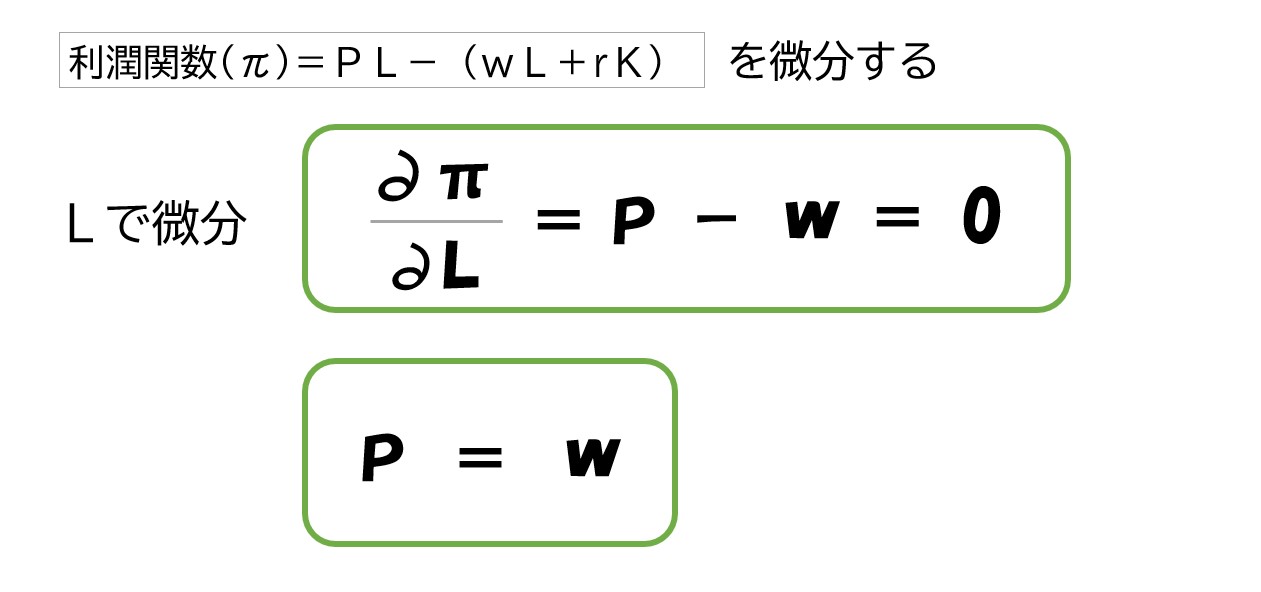
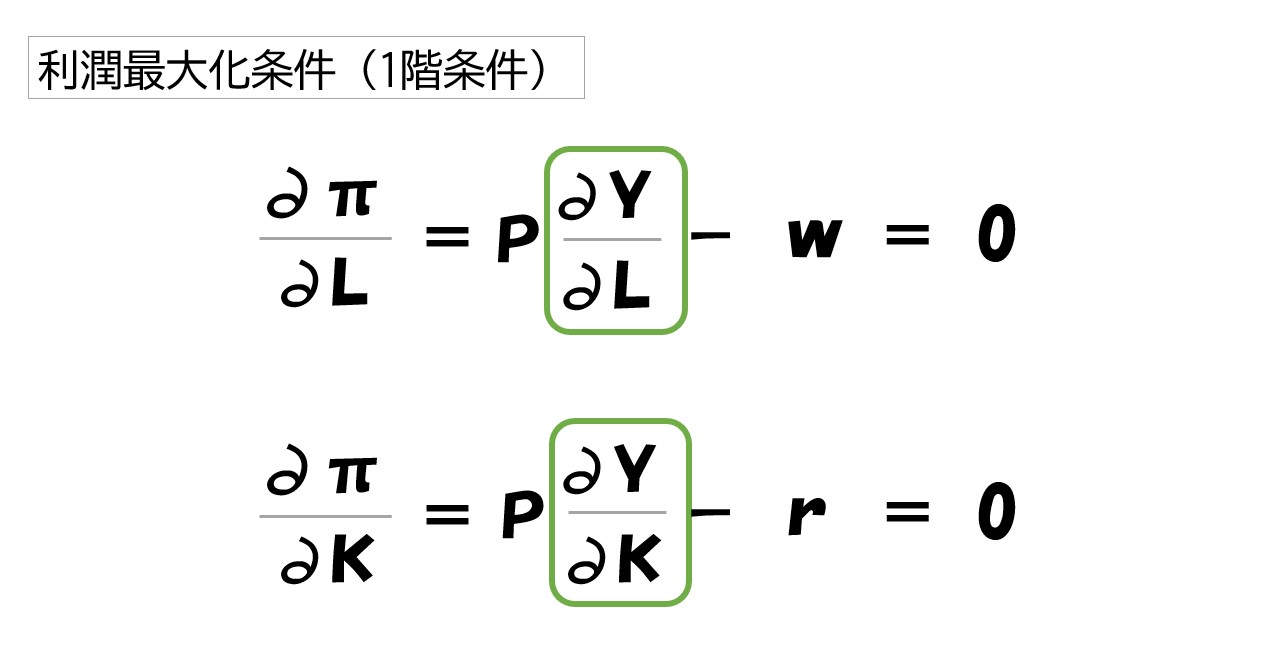

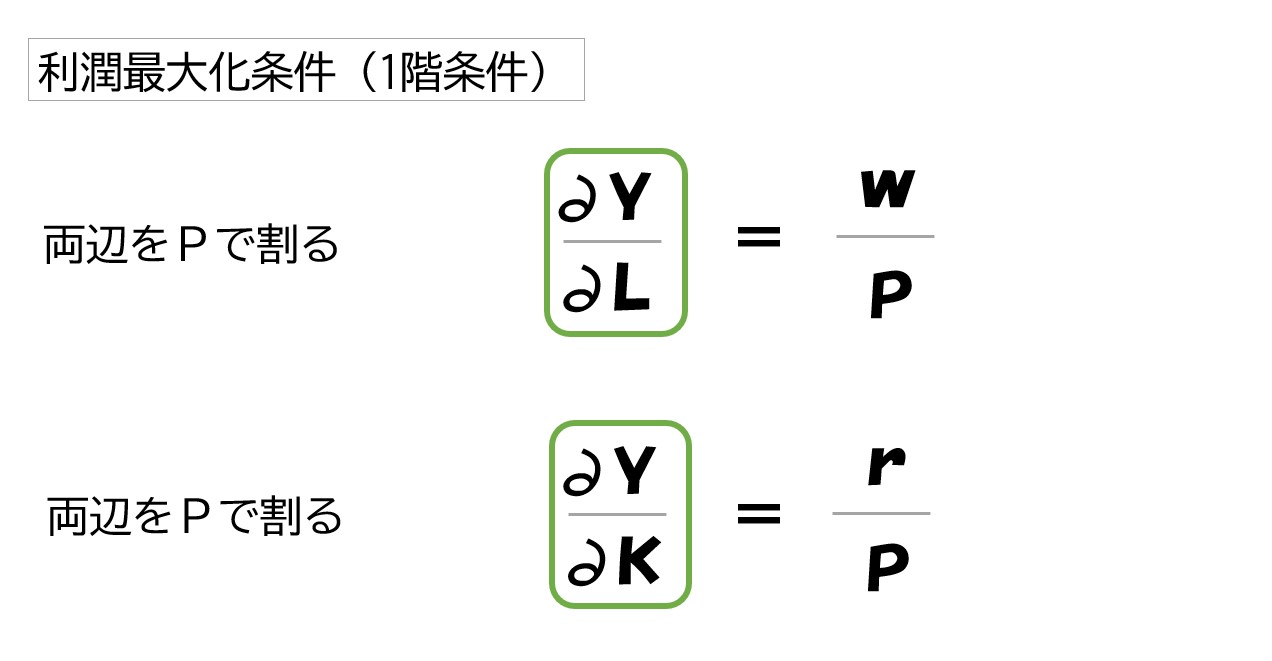


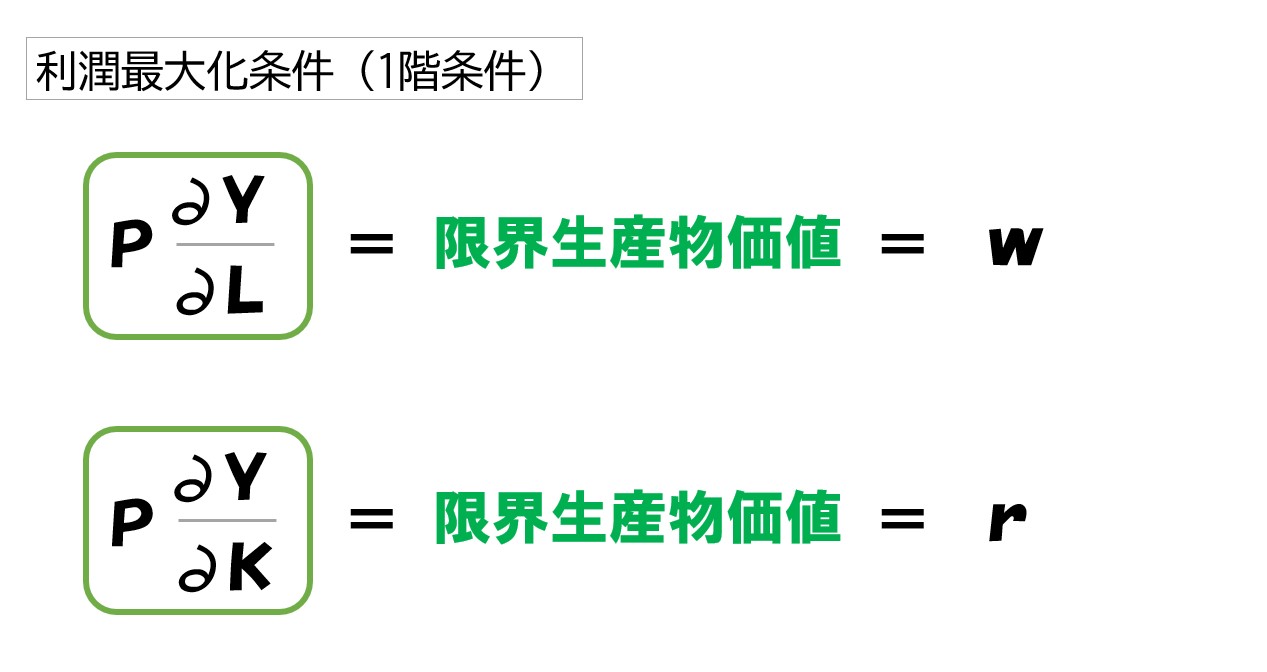
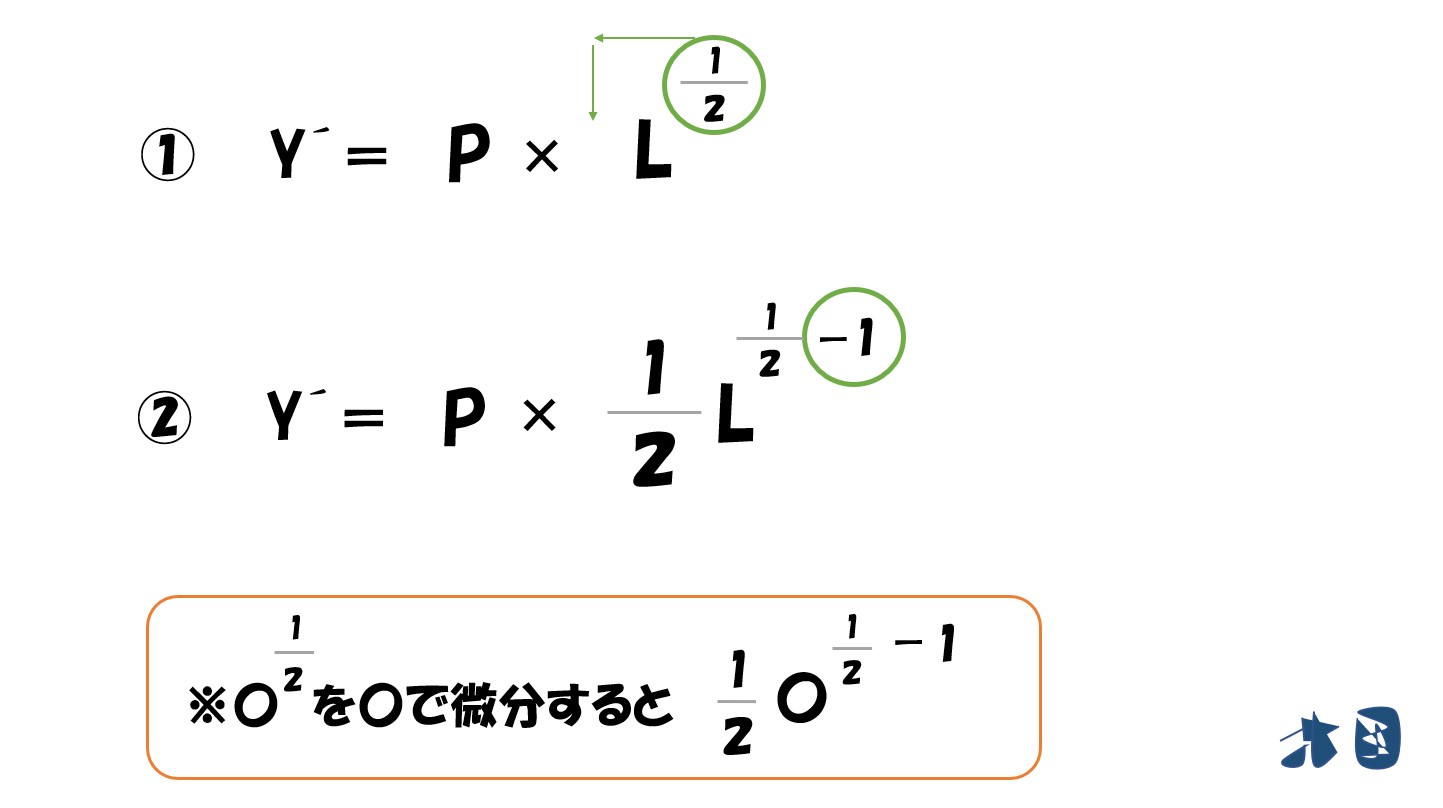
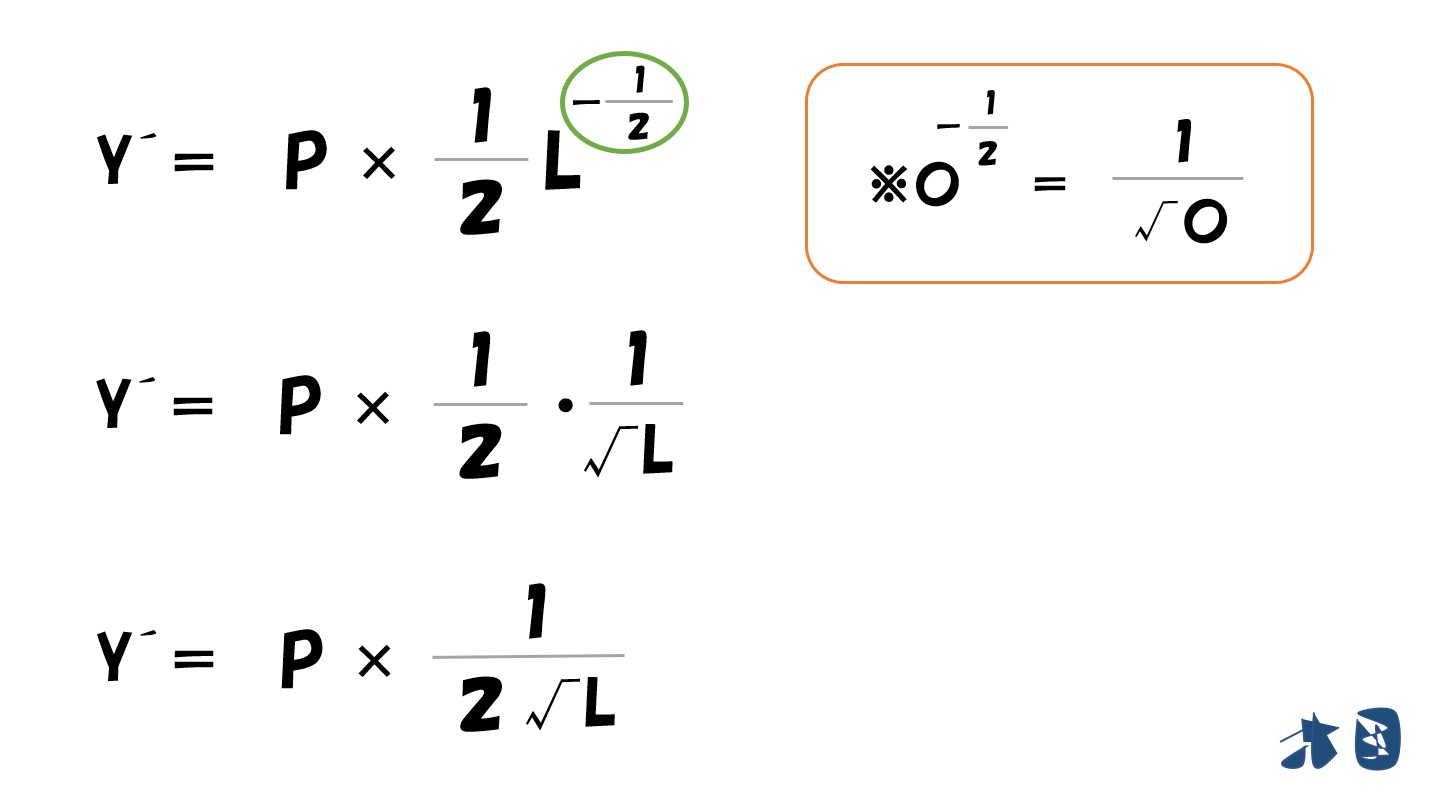

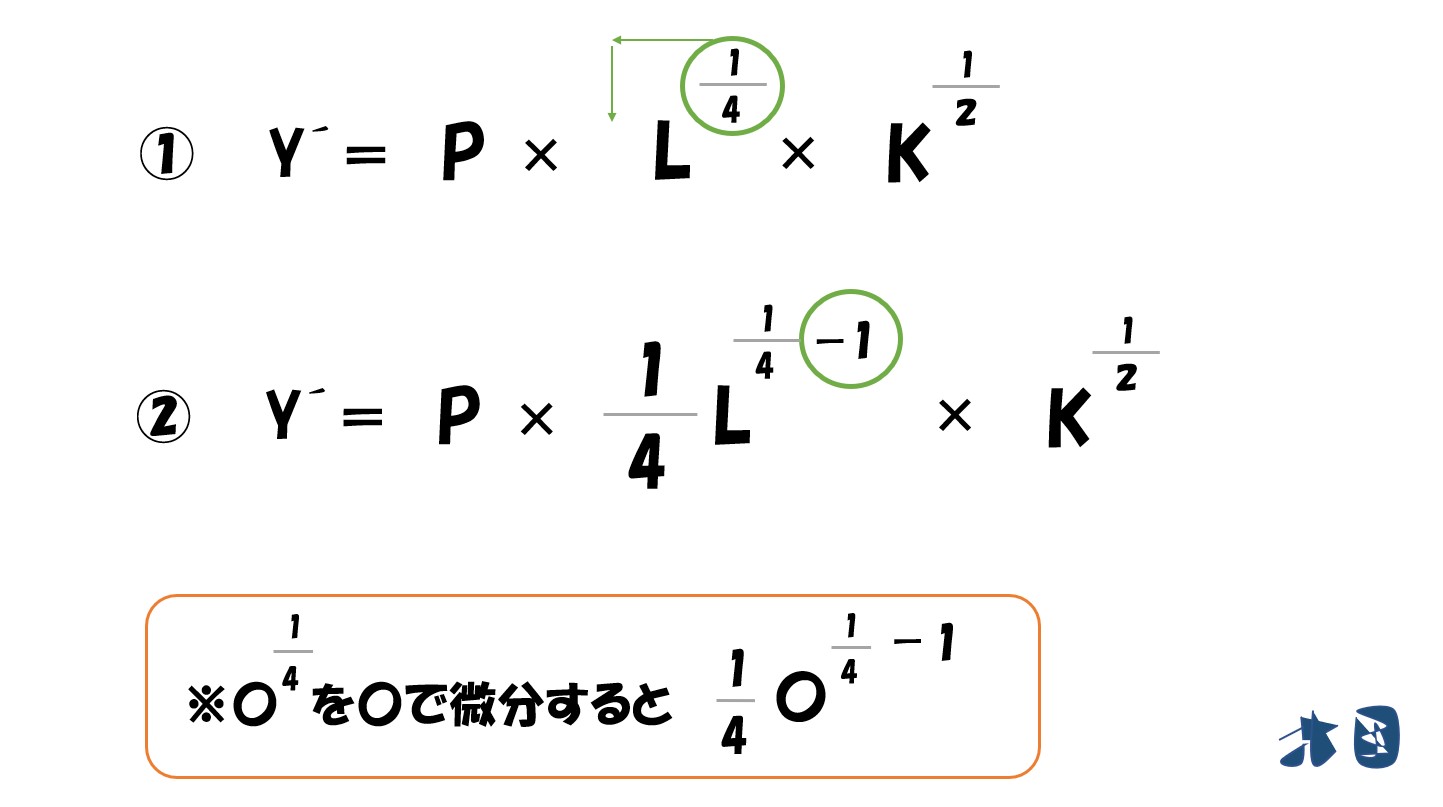
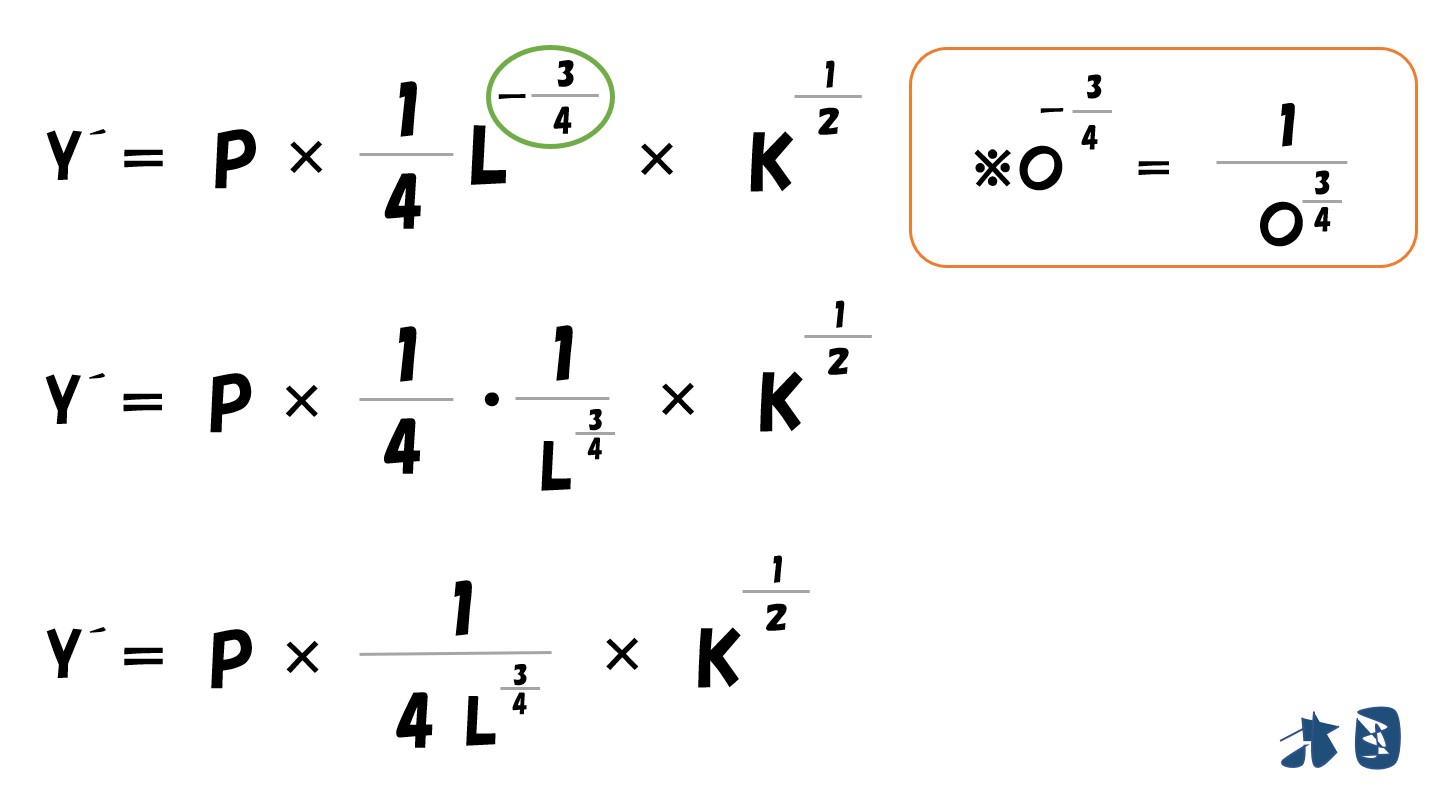
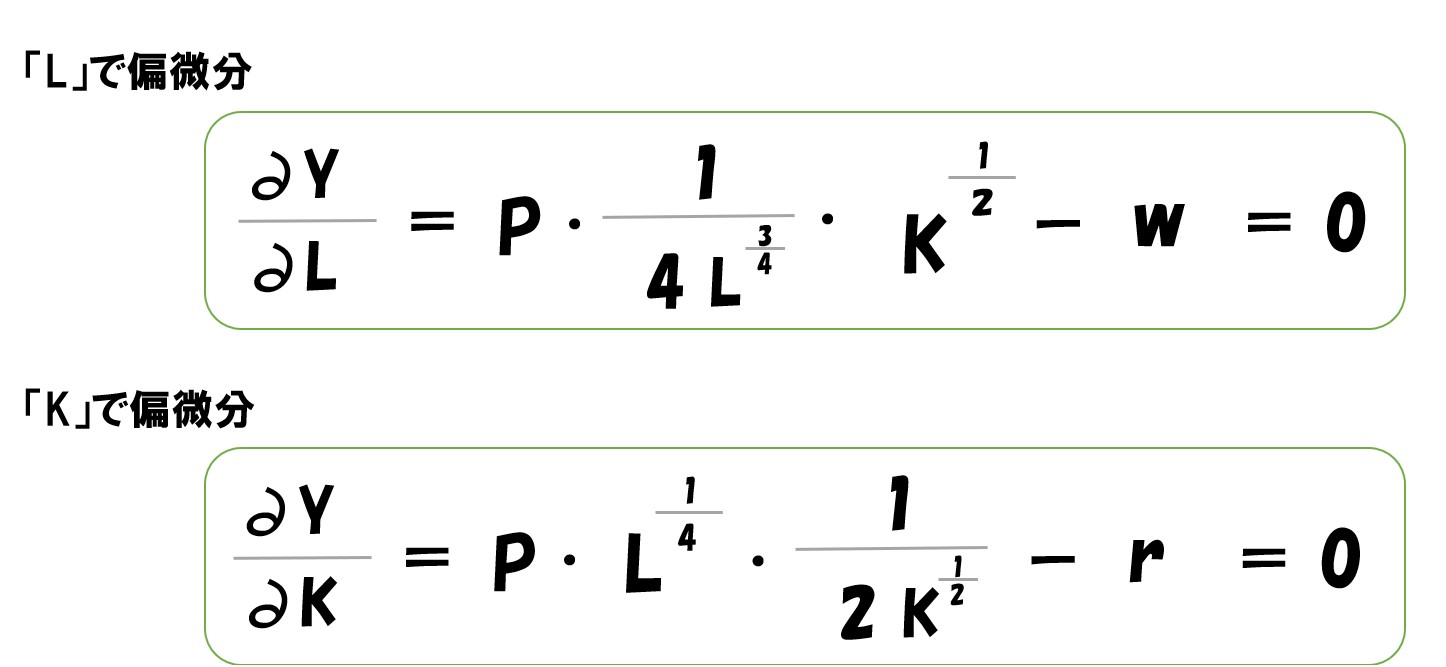
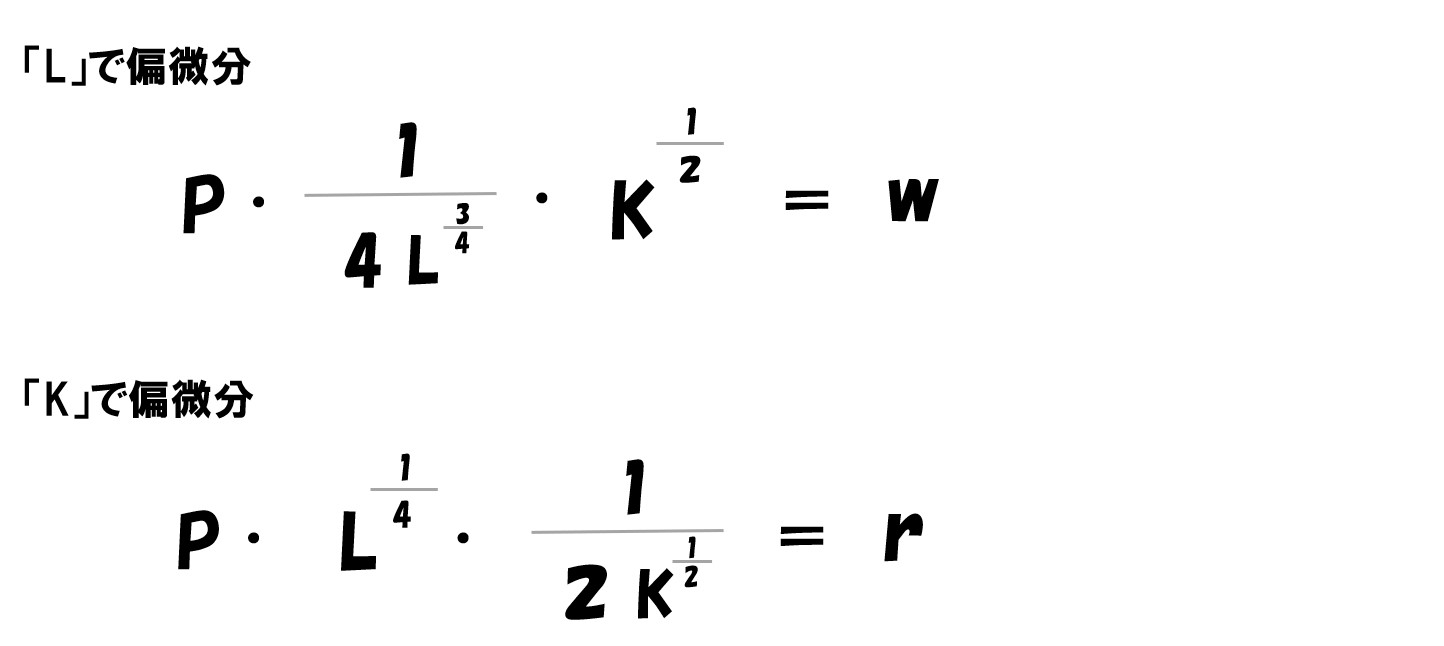
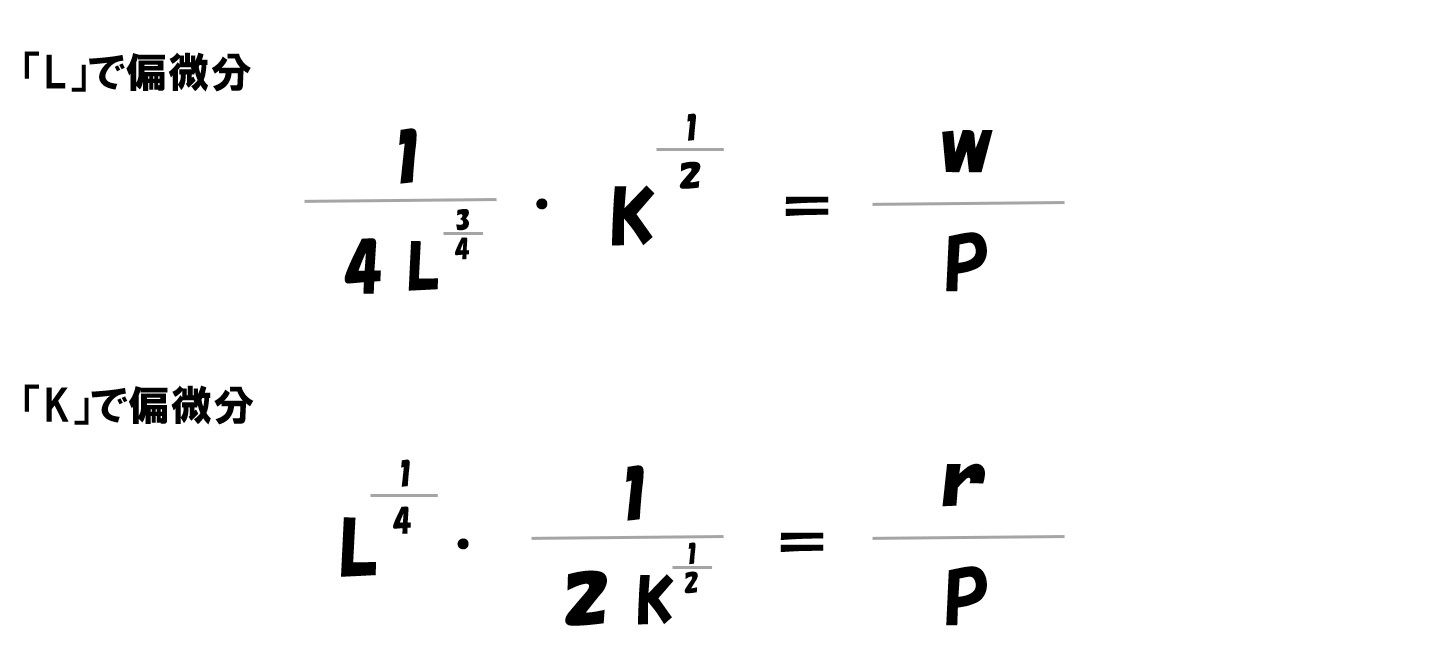
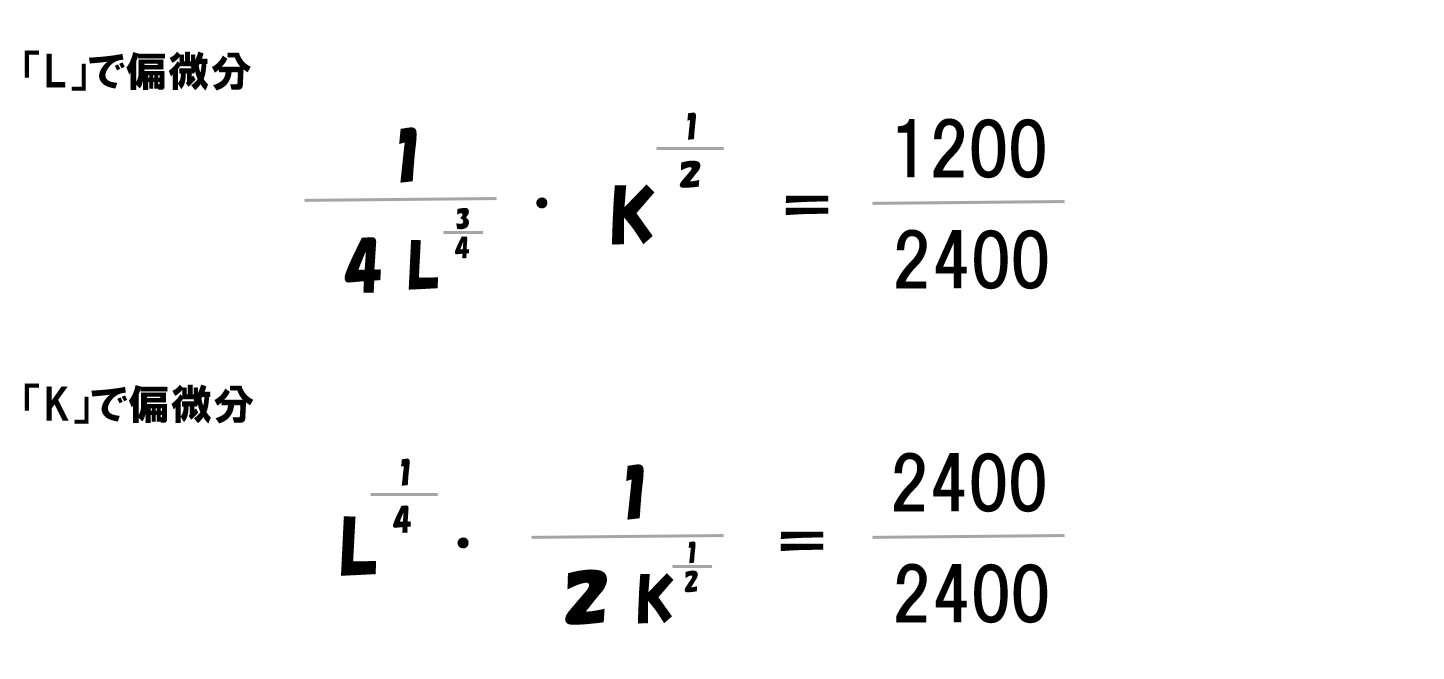
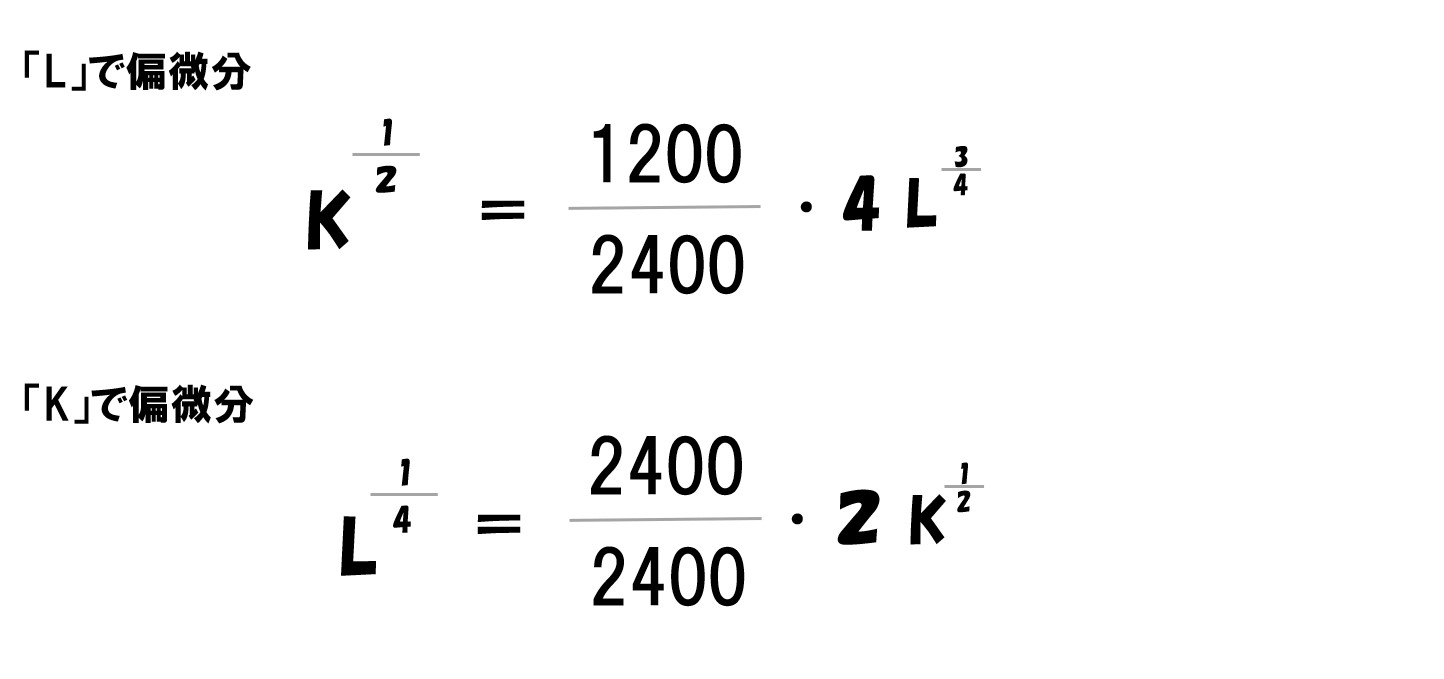
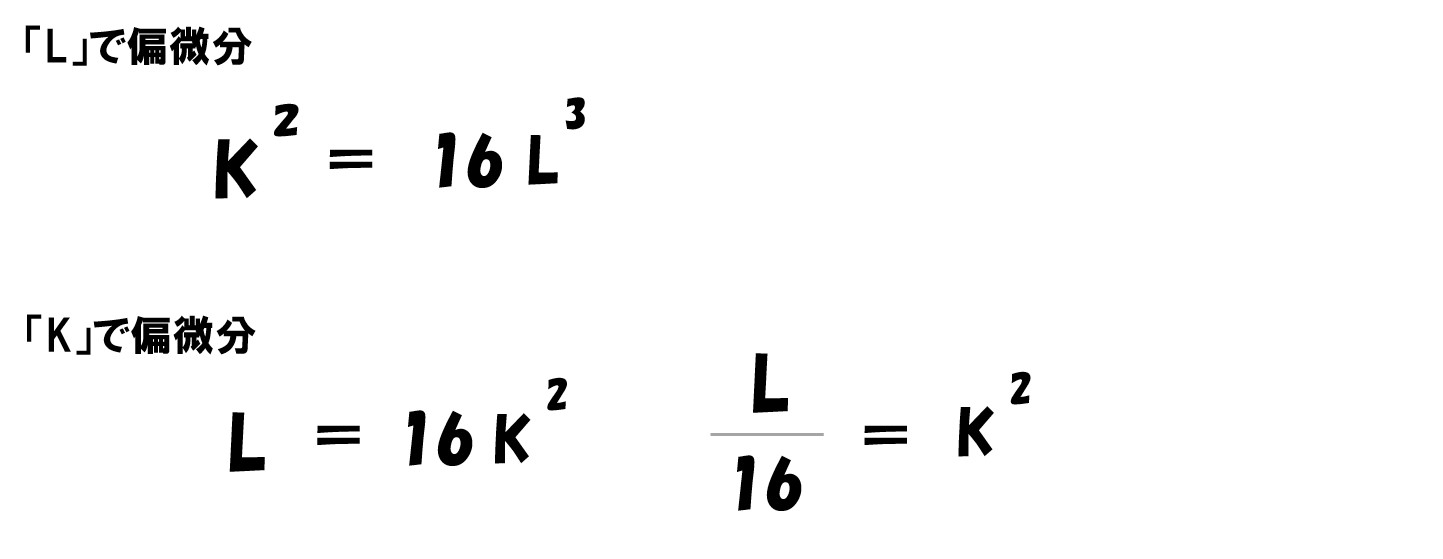

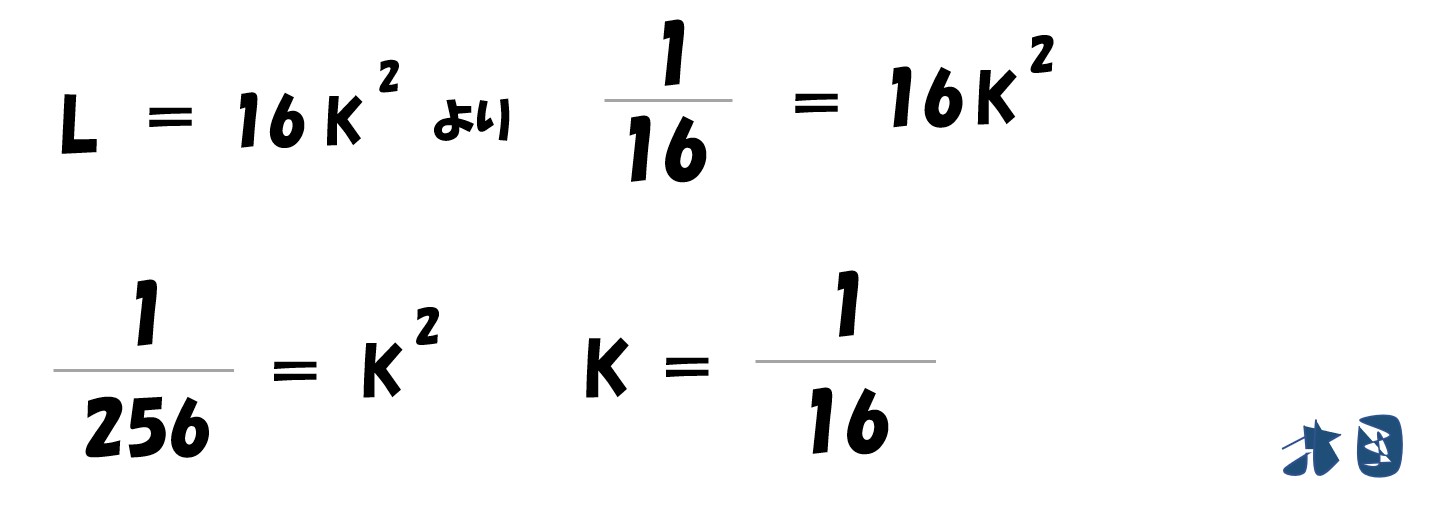
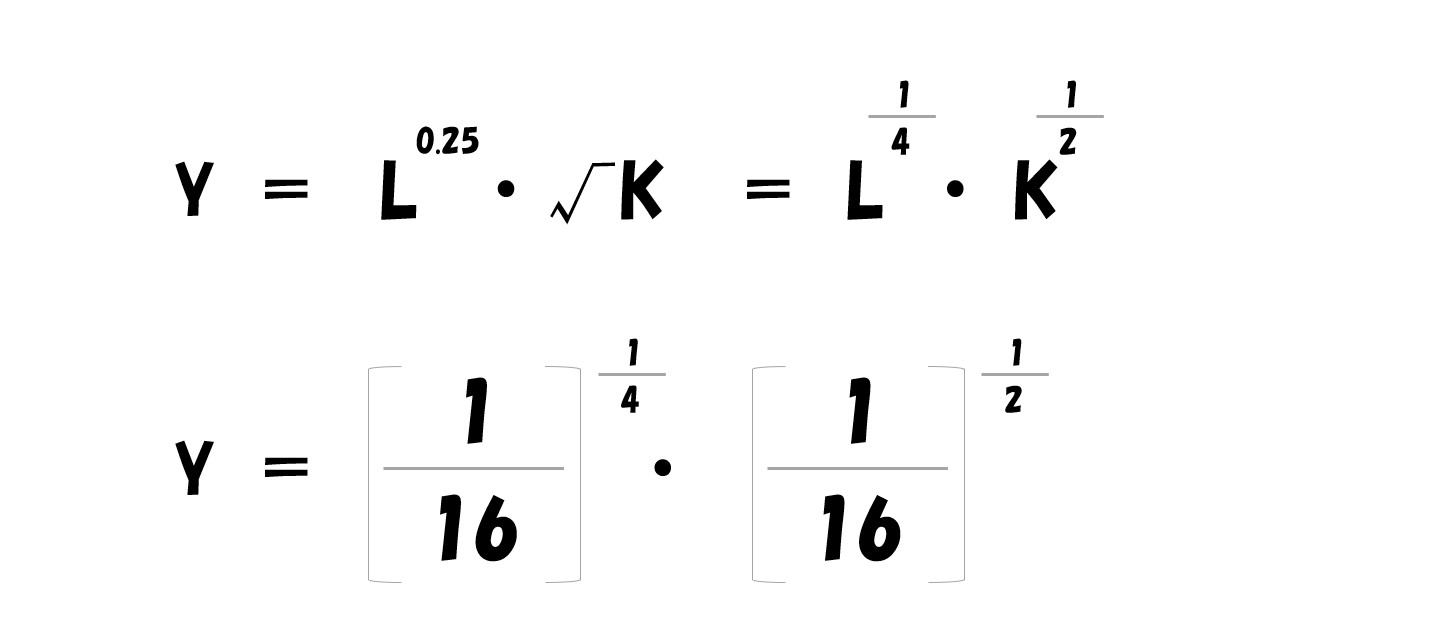
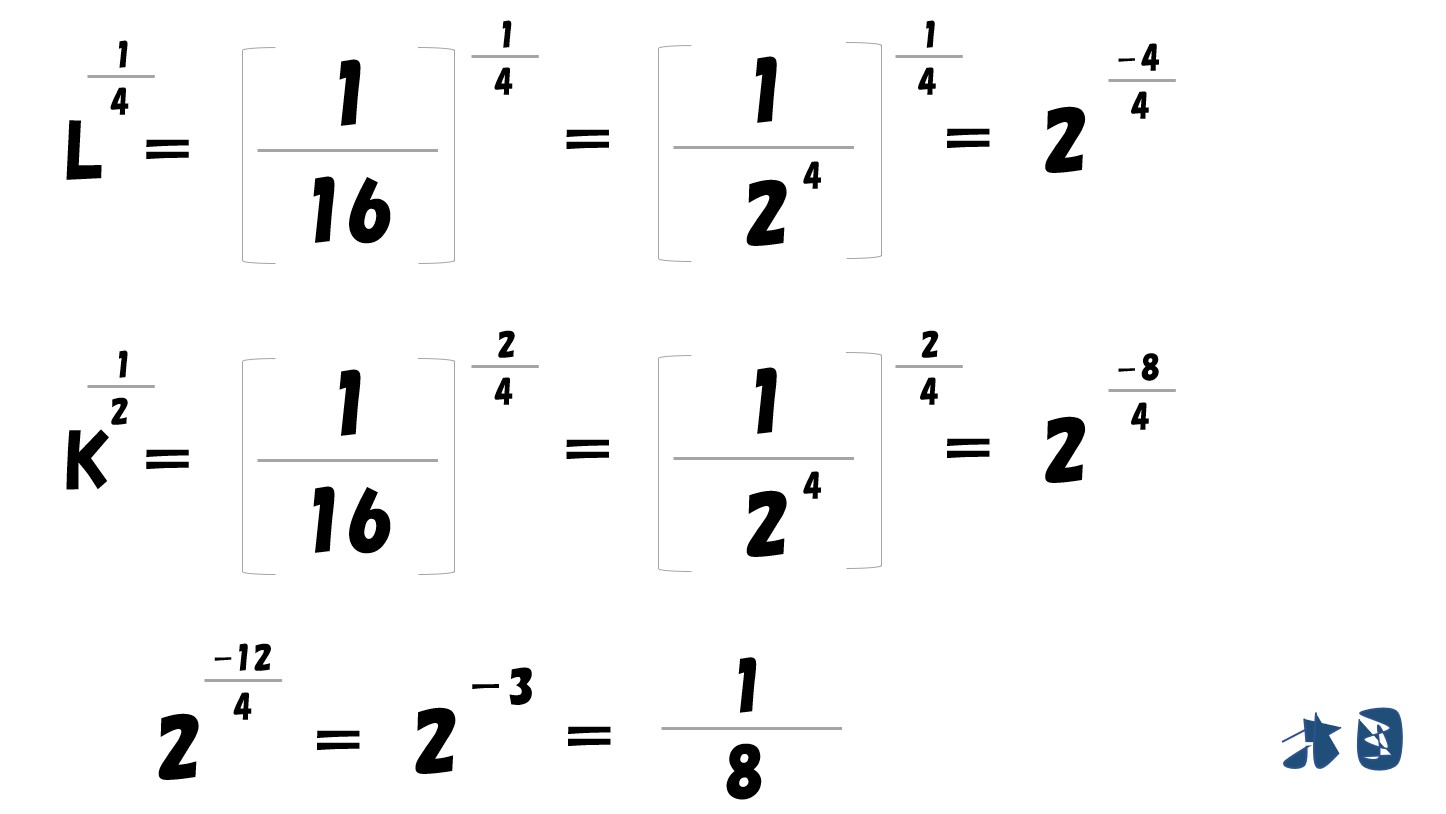
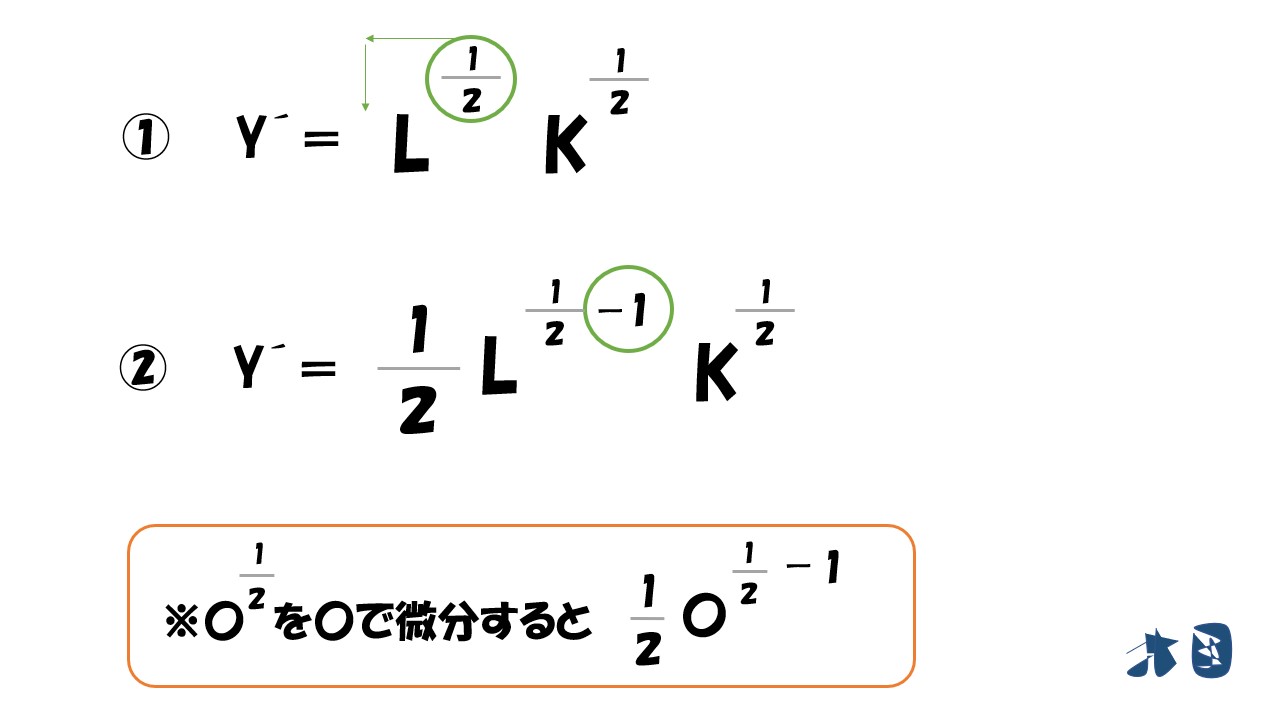


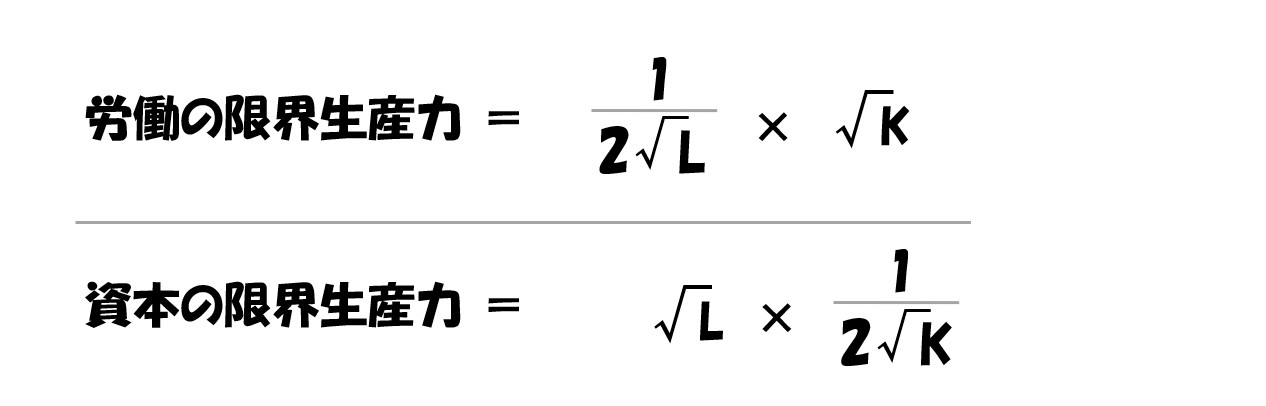
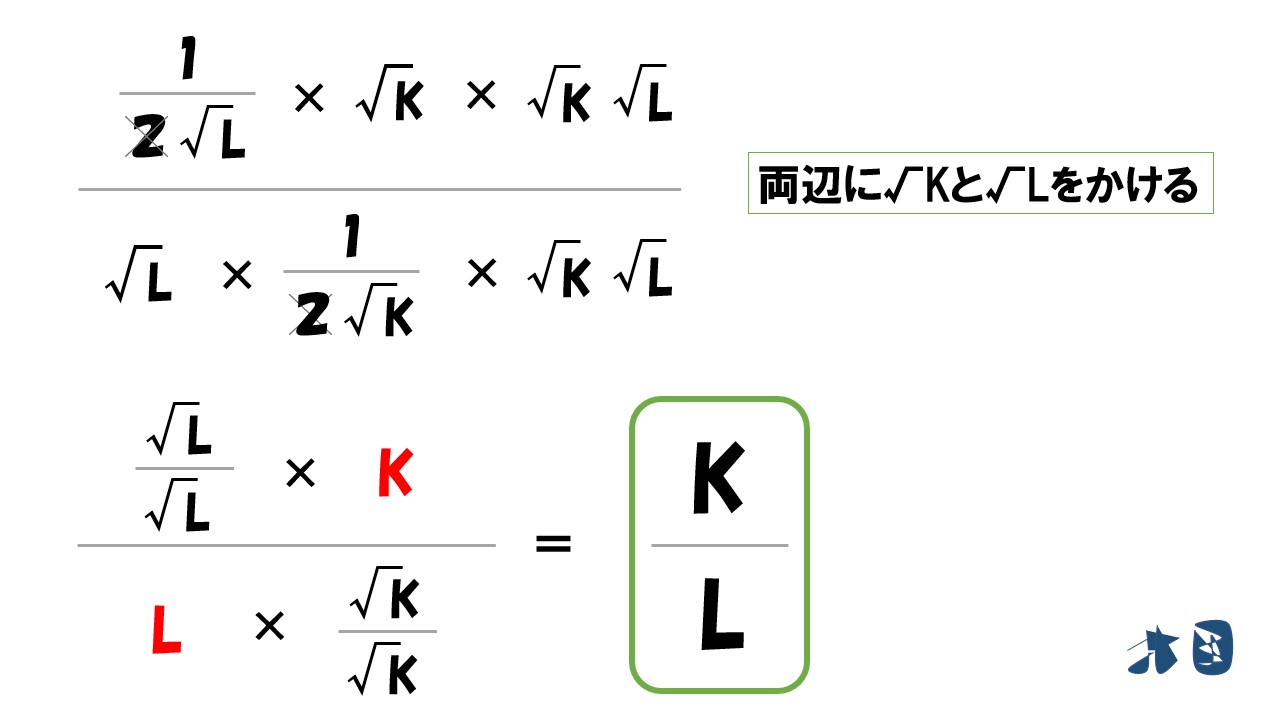
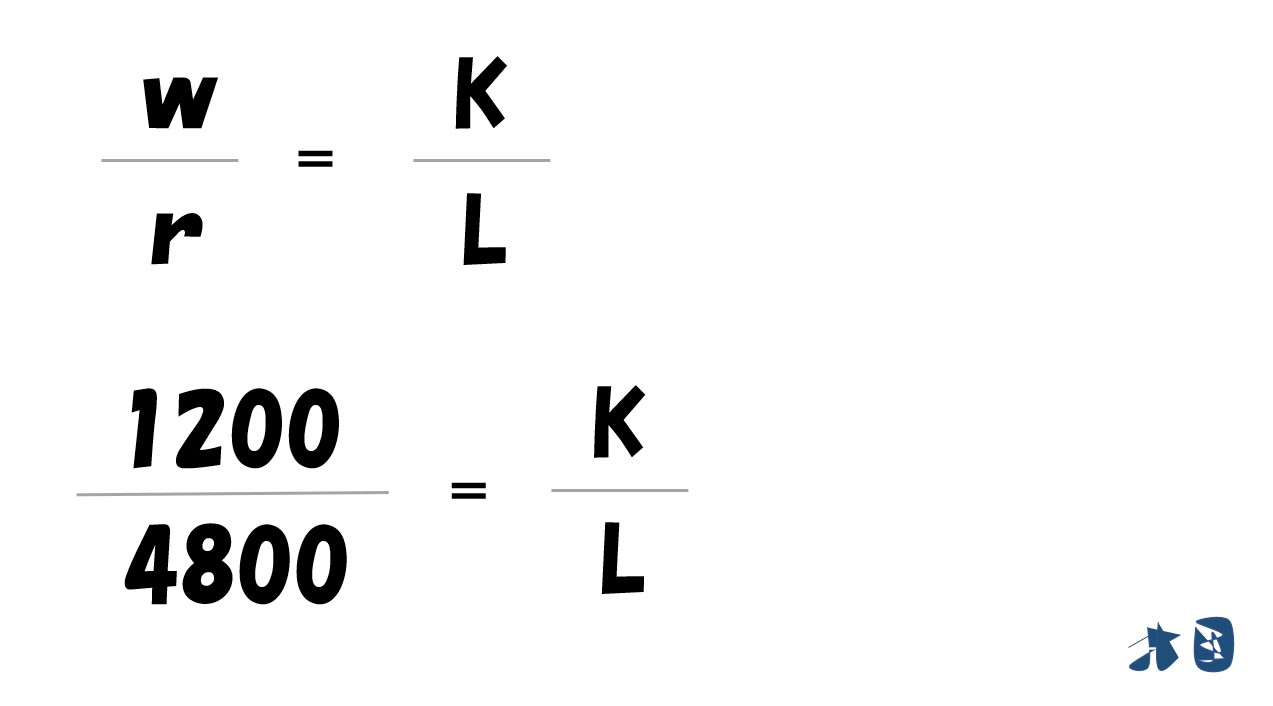
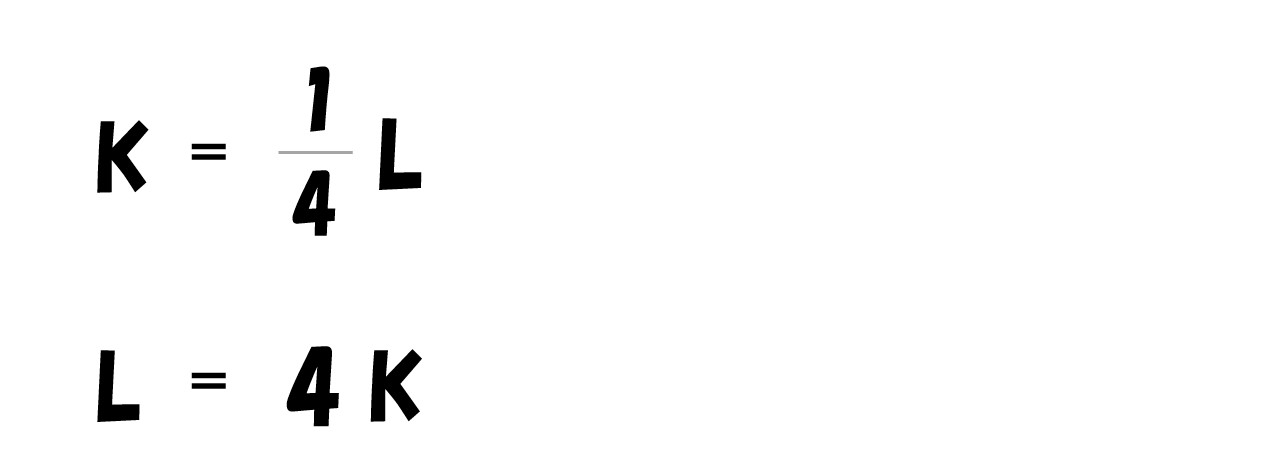
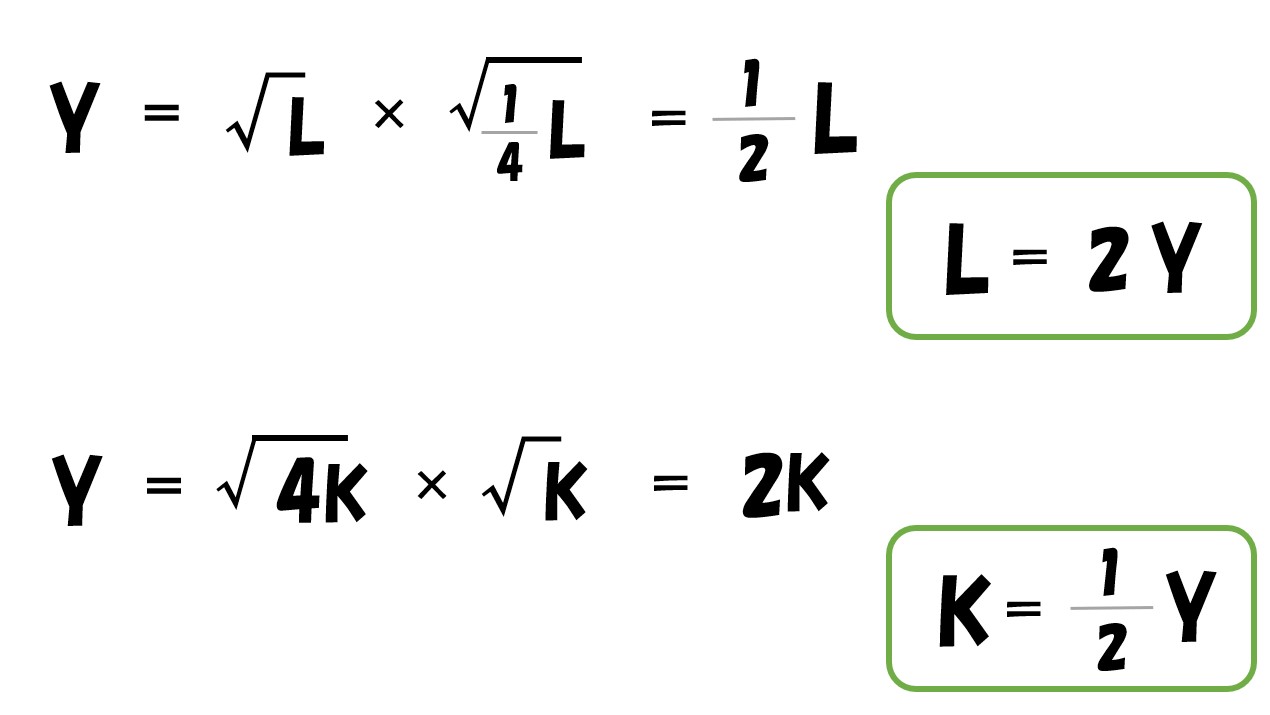
9784915787126
返信削除公共経済学 (新経済学ライブラリ) (日本語) 単行本 – 1990/11/10
常木 淳 (著)
2002年第2版
林正義 小川光 別所俊一郎 公共経済学 有斐閣 2010/1
返信削除JGPは最低賃金を設定する方法の中でベスト
返信削除さらにインフレより物価の安定が大事で
完全雇用がその安定をもたらします
運営は地域に任されます
ラーナーはインフレ研究の嚆矢
公共経済学
返信削除public economics