https://analytics-notty.tech/reason-for-consent-that-area-of-circle-becomes-pir2/
円の面積がπr^2になる納得の理由 – 図形を使った証明
2018年9月8日
この記事ではこんなことを紹介しています
「円の面積の公式である
ここではその理由を、図形を使って視覚的に納得できる説明を紹介します。
証明には小学校の算数の知識までしか使わないので、小学生に理由を聞かれたときにも使えます。
私ははじめてこの説明を聞いたとき、感動しました。
- 1. 円の面積が
πr2 になる理由を説明できますか? - 2. 図形を使って円の面積の公式を証明する
- 2.1. 輪を作って棒にする
- 2.2. 三角形の面積を求めれば…
- 3. まとめ
円の面積がπr2 になる理由を説明できますか?
ここでの主役は、円の面積
です。

もはやいつ習ったかも忘れたぐらい、超基本的な公式の一つですよね。(小学校高学年くらいで習うんでしたっけ?)
しかし、なぜ、
円の面積は円周率
になるかを小学生に説明するには、どうすればよいでしょうか?
実は、すごく面白くて、納得のいく説明があるんです。
ここでは、それを紹介します。
スポンサーリンク図形を使って円の面積の公式を証明する
ここでは、図形を使って円の面積の公式を証明していきます。
まずは、下の図のような普通の円を用意しましょう。
半径は
輪を作って棒にする
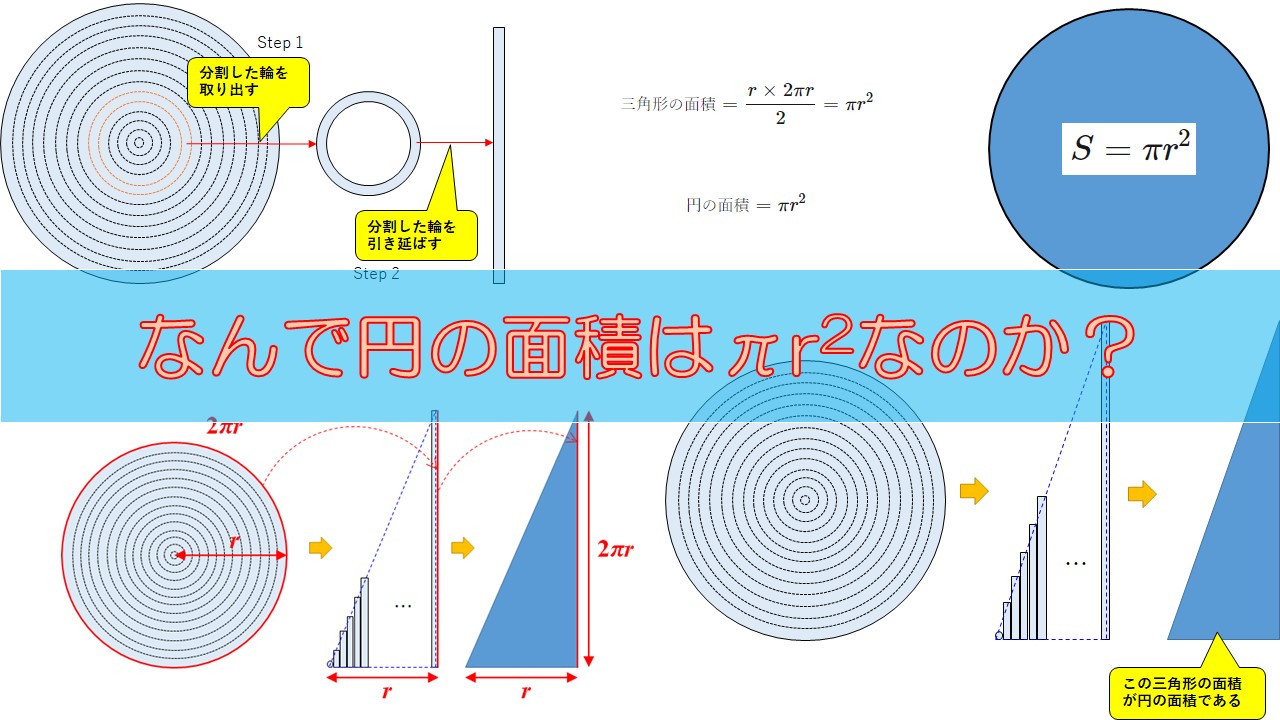
下の図のように、この円からたくさんの輪を作るように切っていきます。
玉ねぎみたいですね。
次に、切った輪を引き延ばして棒にしましょう。
これをすべての輪について行い、順番に並べていきましょう。
ただし、一番内側の中心は、すごく小さいのでここだけはそのままでよいでしょう。
では、具体的に引き延ばした1本の棒について、長さを考えましょう。
例えば、内側から数えて5番目の輪について考えましょう。
この輪の中心からの距離は
このとき、輪を棒にしたときの長さはどうでしょうか?
これは、円の円周の長さを考えれば分かりますね。
円周の長さは、
です。
ですので、内側から数えて5番目の輪の長さは
では、10番目の輪の長さはどうでしょうか?
この輪の中心からの距離は5番目の輪の2倍であることはすぐに分かるでしょう。
よって、長さも2倍になります。
このように、短い方から棒を並べていったとき、直線的(線形)に長さが伸びていくことがわかります。
三角形の面積を求めれば…
ここまできたら後は、下の図の三角形の面積を求めれば、円の面積が求まることがわかります。
三角形は円から作られたものなので、当然面積は変化していないからです。
では、三角形の面積を求めるため、高さと底辺の長さを考えます。
下の図から分かるように、底辺は円の半径と等しくなるはずですね。
では、高さはどうでしょう。
これは、円の円周と同じ長さになることがわかります。
これで三角形の面積を求めるための準備ができました。
底辺の長さが
です。
よって、この三角形の面積は、元の円の面積と同じですので、
となります。
どうでしょうか?!見事に円の面積の公式が導かれました!
まとめ
- 円の面積の公式
S=πr2 は図形を使って視覚的に説明できる - ステップ①:円を輪の形にいくつも分割して、棒状に引き伸ばす
- ステップ②:棒を短い方から順に並べていき、三角形を作る
- ステップ③:三角形の面積は円の面積と等しいため、三角形の面積を求めればよい
0 件のコメント:
コメントを投稿